Cours de Logarithme en Ligne par les Meilleurs Professeurs - Logarithme

Déf fondamentale

Dans ce cours, nous abordons le concept de logarithme et ses propriétés. Le logarithme naturel, noté ln, est une fonction définie sur les nombres réels strictement positifs. Il associe à tout nombre réel positif x, l'unique solution de l'équation E2y = x pour un y donné. Par exemple, si nous avons E2y = 2, nous pouvons utiliser le logarithme de 2 (log 2) pour représenter la solution. Le logarithme inverse de l'exponentielle est également une propriété importante. Mathématiquement, pour tout x positif, l'exponentielle de log x est égale à x. De même, pour tout x appartenant à R, le logarithme de l'exponentielle de x est égal à x. Ces deux fonctions sont donc réciproques l'une de l'autre, tout comme la racine carrée et le carré. Cependant, il est important de noter que le logarithme est uniquement défini pour les x positifs, contrairement à l'exponentielle qui est définie pour tous les réels. Nous avons également mentionné quelques valeurs particulières telles que log 1 = 0, log e = 1 et log(1/e) = -1. Il est crucial de faire attention aux ensembles d'existence pour ces égalités, car ils diffèrent pour le logarithme et l'exponentielle. En résumé, le logarithme est une fonction qui permet de trouver l'unique solution d'une équation exponentielle et possède une relation réciproque avec l'exponentielle. Il est important de prendre en compte les ensembles de définition pour éviter les erreurs.

Simplifier des expressions

Dans ce cours, nous traitons des propriétés et des méthodes pour résoudre des inéquations avec des exponentielles et des logarithmes. Voici un résumé SEO-friendly des différentes équations et inéquations traitées dans la vidéo : 1. Équation : ln(x) = 2 - Composez par l'exponentielle pour obtenir x = e^2. 2. Équation : e^x + 1 = 5 - Composez par le logarithme pour obtenir x + 1 = ln(5). - Résolvez pour x en soustrayant 1 de chaque côté : x = ln(5) - 1. 3. Équation : 3ln(x) - 4 = 8 - Divisez par 3 pour obtenir ln(x) - 4/3 = 8/3. - Composez par l'exponentielle pour obtenir x = e^(4/3). 4. Inéquation : ln(6x - 1) > 2 - Vérifiez que l'expression à l'intérieur du logarithme est strictement positif (6x - 1 > 0). - Composez par l'exponentielle pour obtenir 6x - 1 > e^2. - Résolvez pour x en trouvant que x > (e^2 + 1)/6. 5. Inéquation : e^x + 5 > 4e^x - Rassemblez tous les termes exponentiels ensemble pour obtenir e^x < 5/3. - Composez par le logarithme pour obtenir x < ln(5/3). 6. Équation : ln(x - 3) + ln(9 - x) = 0 - Rassemblez les termes logarithmiques pour obtenir ln((x - 3)(9 - x)) = 0. - Composez par l'exponentielle pour obtenir (x - 3)(9 - x) = 1. - Résolvez l'équation quadratique pour trouver les solutions x1 = 6 + racine(8) et x2 = 6 - racine(8). - Vérifiez que ces solutions sont dans l'intervalle valide (3, 9). 7. Inéquation : ln(3 - x) - ln(x + 1) < 0 - Vérifiez les valeurs possibles pour x (3 - x > 0 et x + 1 > 0), ce qui donne -1 < x < 3. - Rassemblez les termes logarithmiques en utilisant la propriété ln(a) - ln(b) = ln(a/b) pour obtenir ln((3 - x)/(x + 1)) < 0. - Composez par l'exponentielle pour obtenir (3 - x)/(x + 1) < 1. - Multipliez par (x + 1) sans changer le sens de l'inégalité (car (x + 1) > 0), ce qui donne 3 - x < x + 1. - Résolvez l'inéquation pour trouver x > 2. Il est important de toujours considérer l'ensemble de définition de l'équation ou de l'inéquation traitée afin d'exclure les solutions invalides. Il est également essentiel de faire attention aux signes lors de la manipulation d'équations et d'inéquations. Le regroupement des termes logarithmiques et exponentiels est une méthode utile pour résoudre ces types de problèmes.

Équations Inéquations

Ce cours sur les inéquations avec logarithmes explique comment résoudre une équation donnée en isolant le terme en ln. Après avoir vérifié l'ensemble de définition de l'inéquation, l'objectif est de composer par l'exponentiel pour isoler le ln. Ensuite, on résout l'équation simple obtenue et on prend en compte l'ensemble de définition initial pour déterminer l'intervalle solution. Attention à bien faire correspondre les ensembles de définition pour éviter les erreurs. Cette méthode consiste donc à isoler le terme en logarithme, composer par l'exponentiel et prendre l'intersection de la solution finale avec l'ensemble de définition initial.

Exposant=Inconnue ?

Ce cours traite de l'utilisation de l'exponentiel et du logarithme pour résoudre des inéquations avec des exposants. Il mentionne que ces calculs sont notamment utilisés en physique, par exemple pour déterminer la durée à partir de laquelle une certaine quantité d'atomes radioactifs a disparu. Pour résoudre ces équations, on utilise la définition de l'exponentiel pour les puissances. Lorsque l'exposant n'est pas un entier, il est défini comme étant égal à e^(B ln A), où e est la constante d'Euler et ln désigne le logarithme népérien. A partir de cette définition, on résout les équations en utilisant les propriétés du logarithme. Il est important de vérifier la cohérence des signes lors de la résolution des équations.

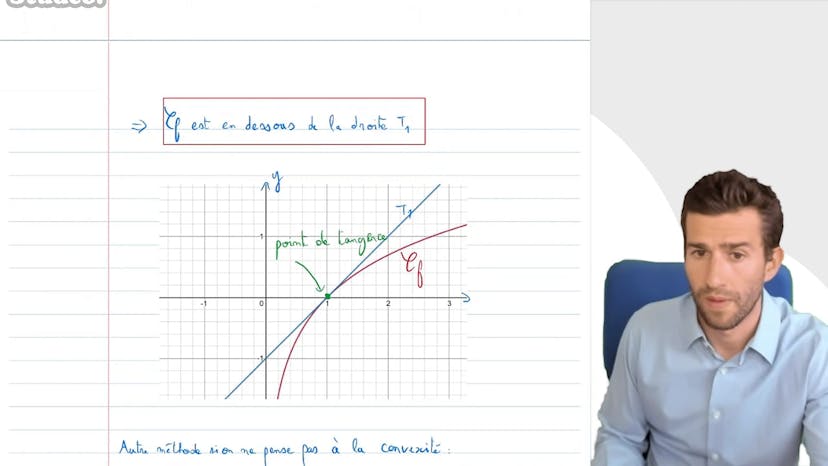
Courbe et Tangentes

Ce cours traite de l'étude du logarithme et de sa tangente en un point précis. On nous demande de trouver l'équation de la tangente au point d'abscisse 1. La fonction logarithme est dérivable sur R*, sa dérivée est 1/x et évaluée en 1, cela donne 1. La position relative de la courbe par rapport à sa tangente peut être déterminée en étudiant la concavité de la fonction. La dérivée seconde est 1/x^2 et est strictement négative pour tout x positif. Cela signifie que la fonction est concave et donc en dessous de toutes ses tangentes, y compris celle au point d'abscisse 1. Une autre approche consiste à étudier les variations de la fonction en calculant sa dérivée. On pose une fonction auxiliaire g(x) = ln(x) - x + 1. En étudiant le signe de g'(x) = 1/(x-1), on peut construire un tableau de variations qui montre que g(x) est inférieure à 0 pour tout x, avec égalité en x=1. En conclusion, la tangente au point d'abscisse 1 de la fonction logarithme a pour équation y = x - 1. Il est préférable de considérer la concavité de la fonction pour déterminer la position relative de la courbe par rapport à sa tangente.

On redécouvre le log ?!

Dans ce cours, on nous demande de déterminer les fonctions qui vérifient f2ab = f2a + f2b et f'(1) = 1. On remarque que la relation fonctionnelle du logarithme ressemble à cette équation. On va donc essayer de redémontrer certaines propriétés du log. Tout d'abord, on démontre que pour toute fonction f non nulle, il n'est pas possible de définir la fonction en 0. On suppose que cela est possible et on utilise la relation donnée pour trouver que f(0) = 0. Si on prend b = 0 et a non nulle, on obtient f(a) = 0. Donc pour tous les réels possibles, f est égal à 0. Cela contredit notre hypothèse de départ que f est non nulle. Donc la fonction ne peut pas être définie en 0. Ensuite, on montre que f(1) = 0. On remplace a et b par 1 dans la relation donnée et on trouve que 2f(0) = f(0), donc f(0) = 0. Enfin, on démontre que f(x/y) = f(x) - f(y). On remarque que cette équation ressemble à la démonstration de log(a/b) = log(a) - log(b). On réapplique la même méthode et on trouve que f(x/y) = -f(y). Cela nous permet de conclure que f(x/y) = f(x) - f(y). En résumé, on a montré que si une fonction vérifie f(2ab) = f(2a) + f(2b) et f'(1) = 1, alors cette fonction a toutes les propriétés du logarithme. On peut donc dire que ces deux conditions suffisent pour définir fondamentalement le log.

Une nouvelle définition de l'exp

Le cours aborde des concepts plus techniques en mathématiques, en particulier sur les logarithmes et les limites. Il explique la propriété principale du logarithme, qui est que le logarithme d'une puissance de A est égal à N fois le logarithme de A. Cette propriété permet de simplifier les expressions mathématiques complexes impliquant des puissances. Le cours souligne également l'importance de connaître les propriétés des logarithmes et des limites pour résoudre des problèmes plus avancés. L'utilisation du logarithme peut aider à simplifier les expressions et à trouver des limites. Le cours montre comment utiliser les propriétés des logarithmes pour démontrer que certaines expressions sont bien définies et pour calculer des limites. Il utilise également des formules du cours pour manipuler les expressions mathématiques et trouver des équivalences. Enfin, le cours conclut en montrant que la limite de log de U, N est égale à A, ce qui démontre l'équivalence entre l'exponentielle et le logarithme. En résumé, le cours explique l'utilisation des logarithmes pour simplifier les expressions mathématiques et trouver des limites. Il met en évidence l'importance de connaître les propriétés des logarithmes et des limites pour résoudre des problèmes plus avancés en mathématiques.