Cours de Divisibilité et Congruences en Ligne par les Meilleurs Professeurs - Divisibilité et Congruences

Division euclidienne

Dans cette transcription vidéo, Paul nous explique la division euclidienne de -534 par 6. Il précise que bien que parfois appelée division euclidienne, l'écriture correcte pour celle-ci est "moins 534 égale à 6 fois Q plus R". Il rappelle également que le dividende est -534, le diviseur est 6, le quotient (Q) peut être positif ou négatif, et le reste (R) doit être compris entre 0 et 6 exclus. Paul procède ensuite à la division. En prenant -53 comme base, il explique qu'il faut multiplier par -8 pour atteindre -534. Le reste est alors -5, et en ajoutant le 4, il descend à -54. Il explique ensuite que pour atteindre 0, on multiplie par -9. Ainsi, le quotient est -89 et le reste est 0. En conclusion, la division euclidienne de -534 par 6 est -534 égale à -89 fois 6 plus 0. Paul recommande d'écrire "+0" pour montrer que l'on a bien compris l'écriture de la division euclidienne. Il termine en disant au revoir et en donnant rendez-vous pour la prochaine fois.

CAPITAL : Reste de 145²⁰²² par 7 ?

Dans cet exercice de congruence, on nous demande de trouver le reste dans la division par 7 de 145 puissance 2022. Pour résoudre cet exercice, il est important de comprendre et connaître une méthode spécifique. Tout d'abord, on simplifie le nombre 145 en le réduisant modulo 7, ce qui donne un reste de 5. On utilise ensuite une technique pour comprendre le comportement des différentes puissances de 5. On remarque un cycle dans les restes des puissances successives, où le reste peut être 3, 4, 2, 3, etc. On utilise alors une règle des congruences qui dit que si A est congruent à B, alors A puissance N est congruent à B puissance N. On applique cette règle pour réduire la puissance 2022 à la puissance 2022 modulo 6, car 5 est plus simple que 145. En étudiant les différentes puissances de 5 modulo 6, on remarque qu'au bout de 6 puissances, on a un cycle qui se répète. On montre alors qu'on a couvert tous les entiers naturels, car tout entier peut s'écrire comme un multiple de 6, un multiple de 6 plus 1, etc. Maintenant, on se concentre sur la puissance 2022. On remarque que 2022 est pair et divisible par 3 (la somme de ses chiffres est 6), donc il est dans la case correspondant à un multiple de 6. Finalement, on conclut que 145 puissance 2022 est congru à 5 puissance 2022, qui est congru à 1. Il est important de comprendre cette méthode en profondeur et de savoir l'utiliser, car elle est très utile pour résoudre de nombreux exercices de congruence et d'arithmétique.

Divisibilité et fraction

Dans cette vidéo, nous abordons un exercice de mathématiques qui concerne la fraction 35 sur n-4. Nous devons déterminer pour quelles valeurs de l'entier n (différentes de 4), cette fraction sera entière. Il est important de prendre en compte que n est un entier relatif et non un entier positif ou naturel. Beaucoup d'élèves se trompent à ce niveau et perdent des points. Pour résoudre cet exercice, nous devons étudier les diviseurs de 35. Les diviseurs de 35 sont 1, 5, 7, et 35. Ils sont également présents dans leur version négative : -1, -5, -7, et -35. Maintenant, nous devons vérifier si n-4 appartient à l'ensemble des diviseurs de 35. Donc nous devons résoudre les équations : - n-4 = 1, ce qui donne n = 5 - n-4 = 5, ce qui donne n = 9 - n-4 = 7, ce qui donne n = 11 Remarquons qu'il ne faut pas inclure 4 dans les réponses car n doit être différent de 4. Finalement, les solutions entières sont les nombres 5, 9, et 11. J'espère que cette vidéo vous a été utile. A bientôt pour une prochaine vidéo.

Divisibilité de n⁵-n ?

Le cours porte sur la factorisation de l'expression a_n = n^5 - n. L'auteur recommande de procéder à une étape de simplification initiale en factorisant l'expression, ce qui permet d'avoir une version plus simple pour les calculs ultérieurs. Ensuite, l'auteur se concentre sur la démonstration que a_n est un nombre pair. Plutôt que de faire une table de congruence, l'auteur remarque que le produit de deux entiers consécutifs (n-1 et n) est toujours pair, car l'un des deux est toujours pair. Par conséquent, a_n est divisible par 2. Pour la question suivante, qui est de montrer que a_n est divisible par 3, l'auteur utilise le fait que n-1, n et n+1 sont trois entiers consécutifs, et donc l'un des trois est toujours un multiple de 3. Par conséquent, leur produit, a_n, est divisible par 3. Enfin, l'auteur utilise les congruences modulo 5 pour montrer que a_n est divisible par 5. En analysant les différentes valeurs possibles pour n modulo 5, l'auteur constate que le produit n*(n-1)*(n+1)*(n^2+1) est toujours congru à 0 modulo 5. Par conséquent, a_n est divisible par 5. En conclusion, l'auteur souligne l'importance d'investir dans une simplification préalable de l'expression, ce qui permet de faciliter les démonstrations ultérieures. L'auteur utilise également les propriétés des entiers consécutifs et des congruences modulo pour simplifier les calculs et parvenir rapidement aux résultats.

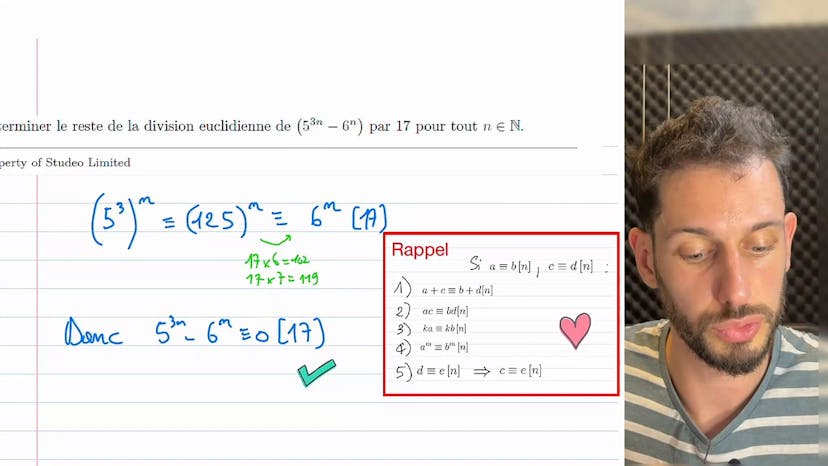
Reste de 5³ⁿ - 6ⁿ par 17 ?

Bonjour à tous, dans cet exercice sur les congruences, nous abordons un exemple de calcul de la division Euclidienne qui peut sembler complexe au premier abord. Il s'agit de trouver le reste de la division de 5 puissance 3n moins 6 puissance n par 17. Plutôt que de nous précipiter dans une table de congruence, nous prenons le temps de réfléchir à une approche plus simple. Nous pouvons examiner séparément les congruences de 5 puissance 3 et 6 puissance n modulo 17 pour essayer de déceler un schéma ou un cycle. Nous commençons par simplifier l'expression 5 puissance 3n en utilisant la propriété des puissances : 5 puissance 3n = (5 puissance 3) puissance n = 125 puissance n. Ensuite, nous utilisons la propriété de congruence pour simplifier modulo 17 en enlevant les multiples de 17. Par exemple, nous pouvons enlever 102 (puisque 17x3 = 51 et 51x2 = 102) et même un peu plus en enlevant 119 (102 + 17) car cela reste éloigné de 125. Ainsi, nous obtenons 125 congru à 6. En conclusion, 5 puissance 3n moins 6 puissance n est toujours congru à 0 modulo 17. Cela signifie que 17 divise toujours cette expression. J'espère que cette explication vous aura été utile. Je vous donne rendez-vous pour de nouvelles vidéos.

Un entier toujours impair ?

Dans ce cours, on nous demande de démontrer que pour tout n, la quantité 3n4 plus 5n1 est impaire. On appelle cette quantité "an" pour la suite de la question. Ensuite, on doit en déduire que ce nombre n'est jamais divisible par nn1. Pour cela, on utilise le fait que nn1 est un produit de deux nombres consécutifs et qu'au moins l'un d'eux est pair. On remarque également que nn1 est la somme des entiers jusqu'à n. On utilise ces propriétés pour démontrer que nn1 ne divise pas an. On conclut en montrant que an est paire et an plus 1 est impaire, et que an plus 1 est toujours divisible par 6, tandis que nn1 est divisible par 2. On utilise des décompositions en facteurs premiers pour arriver à ces conclusions.

Piège à éviter : degré 2 !

Dans cette vidéo, nous abordons un exercice mathématique qui peut sembler difficile et effrayant. Il s'agit de déterminer les solutions d'une équation polynomiale avec des congruences. Tout d'abord, il est conseillé de réécrire l'équation en utilisant des lettres plus conventionnelles pour faciliter la compréhension. Ensuite, nous devons appliquer les méthodes classiques pour résoudre le problème en utilisant une table des congruences. Nous pouvons également essayer de factoriser l'équation pour trouver une solution évidente. Si cela ne fonctionne pas, nous continuons avec la table des congruences en testant différentes valeurs pour x. Après avoir rempli la table, nous constatons que les valeurs de x² plus x ne sont jamais congruentes à 3 modulo 5. Par conséquent, l'ensemble des solutions est vide. Il est important de comprendre la démarche de résolution plutôt que de se concentrer sur les concepts mathématiques complexes. En utilisant une approche méthodique et réfléchie, nous pouvons surmonter les difficultés et résoudre ce type de problème. En conclusion, bien que cet exercice puisse sembler intimidant, il est essentiel d'avoir confiance en sa capacité de réflexion et de prendre le temps d'analyser les différentes possibilités. J'espère que ce résumé vous a été utile et je vous invite à me rejoindre dans ma prochaine vidéo.

5²ⁿ, 2²ⁿ ... et des congruences !

Dans cet exercice de congruence, on nous demande de déterminer quand l'expression 2 puissance 2n + 2 puissance n + 1 est divisible par 7. Pour simplifier, nous remplaçons 2 puissance 2n par 4 puissance n et nous cherchons à comprendre le comportement de 4 puissance n et de 2 puissance n. Nous constatons que 4 puissance n suit un cycle : 4 puissance 1 est congruent à 4, 4 puissance 2 est congruent à 2, et 4 puissance 3 est congruent à 1. Donc, nous avons 4 puissance 3k qui est congruent à 1, 4 puissance 3k + 1 qui est congruent à 4, et 4 puissance 3k + 2 qui est congruent à 2. Quant à 2 puissance n, nous remarquons qu'elle suit également un cycle de taille 3 : 2 puissance 3 est congruent à 1, 2 puissance 3k + 1 est congruent à 2, et 2 puissance 3k + 2 est congruent à 4. En combinant ces résultats, nous concluons que pour tout entier n qui est égal à 3k, 3k + 1 ou 3k + 2, l'expression 2 puissance 2n + 2 puissance n + 1 est congruente à 3 modulo 7. En résumé, l'expression est divisible par 7 pour tous les entiers n qui ne sont pas multiples de 3 (c'est-à-dire les pairs et les entiers qui laissent un reste de 1 ou 2 lorsqu'ils sont divisés par 3).