Cours de Convexité en Ligne par les Meilleurs Professeurs - Convexité

Convexité et f''

La convexité d'une fonction est un concept important en mathématiques. Pour déterminer si une fonction f(x) est concave ou convexe, il suffit d'observer le signe de la dérivée seconde de la fonction. Dans le premier exemple, la fonction f(x) = (1/3)x^3 - (3/2)x^2 + 2x + 1 est un polynôme dérivable deux fois. En dérivant deux fois la fonction, on obtient f''(x) = 2x - 3. On remarque que f''(x) est positif pour x > 3/2 et négatif pour x < 3/2. Par conséquent, la fonction f(x) est concave lorsque x < 3/2 et convexe lorsque x > 3/2. Dans le deuxième exemple, la fonction f(x) = 3x - 3x^(3/2) est définie sur l'ensemble des réels positifs (r*+). En dérivant et en calculant la dérivée seconde, on obtient f''(x) = -9/(4√x). Comme racine de x est toujours positive, on en déduit que f''(x) est toujours négatif. Ainsi, la fonction f(x) est concave sur tout son ensemble de définition. 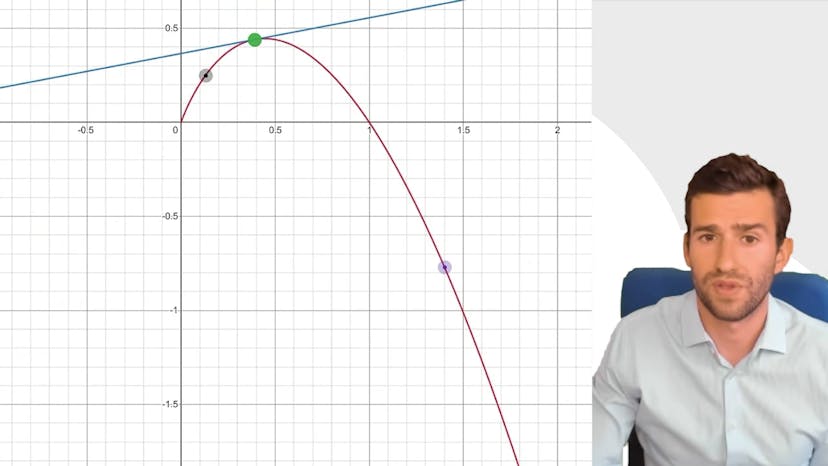La concavité d'une fonction peut être interprétée en termes de tangentes. Lorsqu'une fonction est concave, la tangente est située au-dessus de la courbe sur tout l'intervalle où la fonction est concave. On dit alors que la tangente est sécante avec la courbe en un unique point, le point de tangence. De plus, la courbe est toujours au-dessus des cordes définies par deux points de la courbe. En conclusion, l'étude de la concavité et de la convexité d'une fonction permet de déterminer la position relative de la tangente par rapport à la courbe. Une fonction concave est en dessous de sa tangente, tandis qu'une fonction convexe présente la situation inverse.

Convexité et Inégalités

Dans ce cours, nous étudions la méthode de la convexité en SEO friendly. La méthode est assez classique et facile à appliquer une fois que l'on maîtrise l'étude de la convexité. Nous commençons par nous intéresser à une fonction f(x) égale à x^3 - 2x^2, qui est un polynôme dérivable deux fois. Nous calculons les deux dérivées de cette fonction : f'(x) = 3x^2 - 4x et f''(x) = 6x - 4. Nous souhaitons étudier le signe de f''(x) pour déterminer la concavité et la convexité de la fonction. En résolvant l'inéquation 6x - 4 > 0, nous trouvons que x > 3/2. En résolvant l'inéquation 6x - 4 < 0, nous trouvons que x < 3/2. Nous en déduisons que la fonction f est concave sur l'intervalle ]-∞, 3/2] et convexe sur l'intervalle [3/2, +∞]. 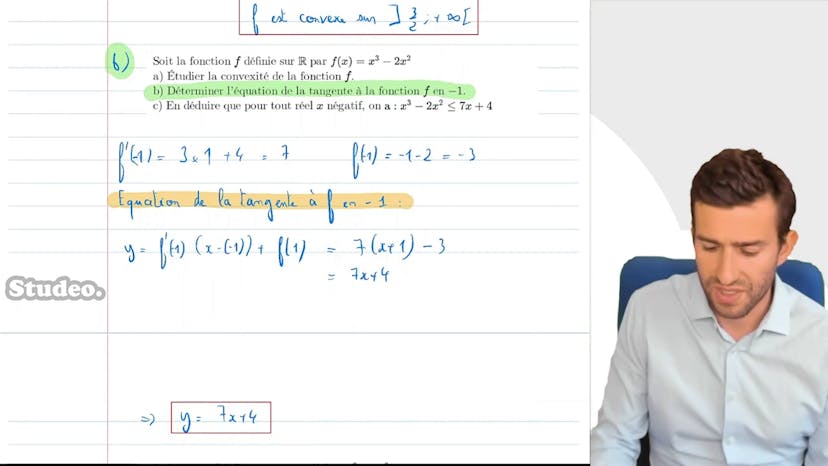Ensuite, on nous demande l'équation de la tangente de f au point -1. En utilisant la formule y = f'(1)(x - (-1)) + f(1), nous trouvons que l'équation de la tangente est y = 7x + 4. Nous devons ensuite déduire que pour tout x négatif, x^3 - 2x^2 < 7x + 4. En analysant cette inégalité, nous observons que 7x + 4 est l'équation de la tangente que nous avons calculée précédemment, et x^3 - 2x^2 est la fonction f. Ainsi, géométriquement, cette inégalité signifie que la courbe représentant la fonction f est située en dessous de sa tangente. Cela est vrai lorsque la fonction est concave, ce qui est le cas sur l'intervalle ]-∞, 3/2]. Par conséquent, nous avons bien l'inégalité souhaitée. Il est important de noter que cette méthode repose sur l'analyse de la convexité de la fonction. Sans cette notion, on ne pourrait pas résoudre l'équation x^3 - 2x^2 < 7x + 4, car elle implique un polynôme de degré 3. Il faut donc toujours penser à la convexité pour résoudre ce type d'équations. En conclusion, la méthode de la convexité nous permet d'étudier la concavité et la convexité d'une fonction, de trouver l'équation de la tangente en un point et d'établir des inégalités entre une fonction et sa tangente. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires.

Points d'Inflexion

Ce cours porte sur la convexité des fonctions et les points d'inflexion. La fonction étudiée est f2x et nous allons la dériver deux fois pour trouver ses variations. Nous commençons par calculer la première dérivée, f', qui est toujours positive car l'exponentielle dans la fonction est positive. Le signe important est celui de "-x plus 1". Ce terme est positif pour x allant de moins l'infini à 1 et négatif sinon. Nous en déduisons que la dérivée est positive pour x < 1 et négative pour x > 1. En utilisant ces informations, nous construisons le tableau de variations de la fonction f. Elle est croissante jusqu'à x = 1, puis décroissante. Son maximum est atteint à x = 1, avec une valeur de 7e-1. Nous calculons également les limites de la fonction aux infinis. Pour x tendant vers moins l'infini, la limite est moins l'infini, tandis que pour x tendant vers plus l'infini, la limite est 0. Nous avons ainsi un tableau de variations complet. Ensuite, nous calculons la seconde dérivée, f'' qui est également dérivable. Le résultat final est 7 fois x moins 2, fois e de moins x. Comme l'exponentielle est positive, le signe dépend de x moins 2. La dérivée est positive pour x > 2 et négative pour x < 2. Nous concluons que la dérivée seconde change de signe en x = 2, ce qui indique un point d'inflexion. Pour trouver les coordonnées de ce point d'inflexion, nous évaluons f(2) qui est égal à 14 moins 2, soit 12. Visuellement, sur le graphique de la fonction, on peut observer que la pente diminue avant le point d'inflexion, puis commence à augmenter après. La courbe de la dérivée seconde confirme cette observation. Les points d'inflexion sont couramment utilisés en physique, notamment dans le titrage pour repérer un changement d'augmentation ou de diminution de la pente de la courbe. Cela conclut notre étude sur la convexité et les points d'inflexion. N'hésitez pas à consulter la FAQ si vous avez d'autres questions.

Intuition et déf

La vidéo traite de la convexité et commence par expliquer que l'on peut comprendre très simplement ce qu'est une fonction convexe ou concave avec l'aide d'un graphique. L'explication visuelle consiste à dire que convex c'est quand ça monte comme ça, et concave c'est quand ça monte mais pas trop vite. La vidéo introduit ensuite la définition mathématique officielle de la convexité, qui consiste à définir une séquente comme toute droite qui relie deux points d'une courbe, et une fonction convexe si, pour tout réel X de l'intervalle I, la courbe est en dessous de cette séquente. La vidéo explique que cette définition s'applique à toutes les fonctions, qu'elles soient continues ou pas. Enfin, la vidéo présente deux exemples de fonctions convexes et concaves, avec des graphiques pour illustrer ces concepts.

Fonctions usuelles

Ce cours aborde les fonctions classiques comme la fonction racine et la fonction log. Les fonctions convexes sont celles qui ressemblent à un sourire, comme x² et exp x, tandis que les fonctions concaves ont une courbe en forme de sourire inversé, comme la fonction racine. La fonction 1 sur x est convexe sur r plus, mais concave sur r moins. Une règle hors programme, mais utile à retenir, est que les racines, comme la racine carrée, sont toujours concaves, tandis que les puissances supérieures strictes à 1 sont toujours convexes sur r plus. Les puissances de x peuvent être traçées pour illustrer cette règle.

Inégalité fondamentale

Dans ce cours, nous apprenons la relation entre une fonction convex et ses séquentes. Pour être précis, nous étudions la différence d'ordonnée d'un point sur le segment bleu et d'un point sur la courbe rouge pour une même abscisse comprise entre l'abscisse de A et de B. Cette différence est plus grande lorsque le point est sur la courbe rouge que lorsqu'il est sur le segment bleu, ce qui montre que la fonction est convex. Nous nommons le point d'abscisse intermédiaire entre A et B "T" et prenons une moyenne pondérée des abscisses pour comparer l'image de ce point sur la courbe rouge à celle de l'équation du segment de la séquente. Nous démontrons ensuite que le lien entre la convexité et la concavité est réciproque. Une fonction convexe est moins concave et vice versa.

Lien dérivation

La convexité d'une fonction dépend de la position entre la séquente et la courbe de la fonction, et non de la continuité ou de la dérivabilité de la fonction. Si f' est dérivable, on peut utiliser une autre définition de la convexité, qui est plus pratique pour les exercices, à savoir f' croissante pour une fonction convex, et f' décroissante pour une fonction concave. Pour une fonction deux fois dérivable, on peut étudier les variations de f'' pour connaître la convexité de la fonction. Si f'' est positive sur les zones où f' est positive, la courbe est convexe. Si f'' est négative sur ces zones, la fonction est concave. On n'a donc plus besoin de comparer la courbe et les droites pour étudier la convexité, mais il suffit de calculer la double dérivée.

Point d'inflexion

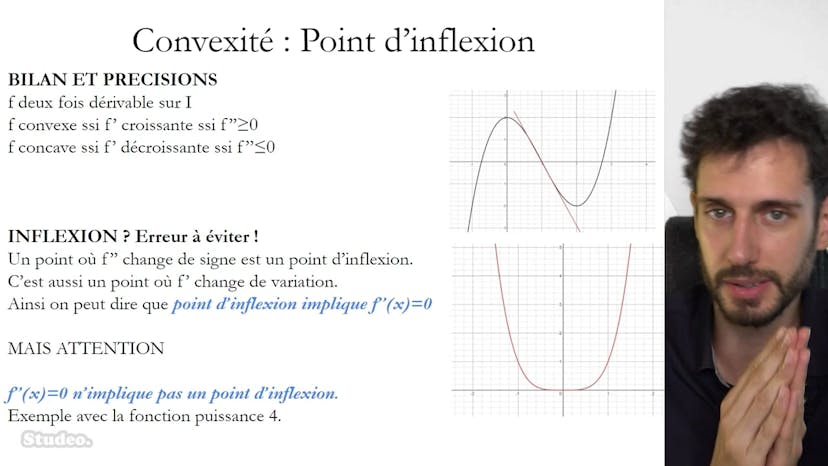
Dans cette vidéo, le concept de point d'inflexion est présenté. Pour qu'un point A soit un point d'inflexion d'une fonction f en 2 fois dérivable, il faut que la courbe cf traverse la tangente TA en A. Cela se produit lorsque la dérivée seconde change de signe en A. Visuellement, on peut observer un changement de comportement entre concavité et convexité à ce point. De plus, le point d'inflexion correspond à un maximum en valeur absolue de la pente de la tangente en ce point. Il est important de noter que f'' de x égal à zéro n'implique pas nécessairement un point d'inflexion, cela dépend du comportement de la fonction autour de ce point.

Convexité étude COMPLETE

Aucun résumé n'est disponible pour cette vidéo

Fonctions cubes et convexité

Le cours aborde différents paramètres (A, B, C, D) et propose une démonstration générale sur les fonctions x³. Il met en évidence l'intuition graphique selon laquelle une fonction x³ avec un coefficient positif est concave, tandis qu'une fonction avec un coefficient négatif est convexe. Pour étudier la convexité de la fonction f, il faut analyser le signe de f prime prime, qui dépend de la valeur de A. Si A est positif, la fonction est concave, alors que si A est négatif, elle est convexe. Une erreur courante est de ne pas distinguer les différents cas. L'exercice demande également d'appliquer ce résultat à un exemple spécifique.

Démo inégalité convexité

Le cours explique comment démontrer que le point M est sur la séquente d'une fonction convex F. Pour cela, on utilise les points a et b associés aux réels x et y et un point M défini par des formules. On montre d'abord que l'ordonnée de M est bien sur la séquente en utilisant des calculs et des formules liées aux moyennes pondérées. Ensuite, on montre que M est sur le segment AB en utilisant l'équation d'une droite passant par a et b et en vérifiant que M satisfait cette équation. Enfin, on conclut que l'image de la piscine de M par la séquente est au-dessus de son image par F, ce qui permet de démontrer que M est sur la séquente de F.