Cours d'apprentissage en ligne

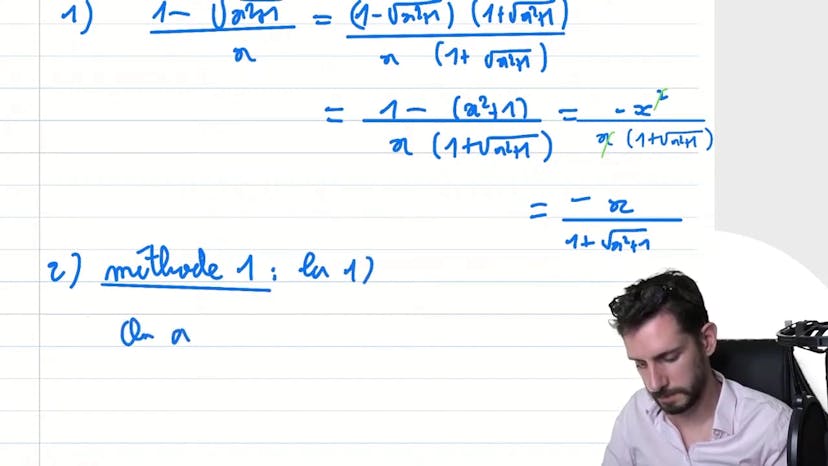
Saut de continuité

Le cours traite de la continuité d'une fonction définie par morceaux. On commence par introduire un exercice simple sur la continuité qui rappelle la définition de la continuité. Ensuite, on donne une fonction définie par f2x égale à une certaine valeur si x est différent de 0, et f2z égale à m si x vaut 0. On explique qu'il est possible d'écrire cette fonction sous une forme différente en utilisant la quantité conjuguée. On présente deux méthodes pour résoudre l'exercice. La méthode 1 consiste à utiliser la quantité conjuguée pour éliminer une forme indéterminée dans la limite de la fonction. La méthode 2 consiste à reconnaître un taux d'accroissement et à utiliser la dérivabilité de la fonction racine pour résoudre l'exercice. On conclut en disant que pour que la fonction f soit continue en 0, il faut que la valeur m soit égale à 0.

TVI et expo

Dans cette leçon, nous étudions le nombre de solutions de l'équation E-x² = E2x-1. Graphiquement, nous avons représenté les deux fonctions E-x² et E2x-1. La première est une courbe en cloche symétrique par rapport à l'axe des ordonnées, tandis que la deuxième est une fonction exponentielle décalée de 1 vers le bas. En examinant le graphique, nous observons qu'il y a une solution autour de 0.552. De plus, pour les nombres négatifs, la fonction E-x² est toujours supérieure à la fonction E2x-1, tandis que pour les nombres positifs, il y a un point d'intersection où les deux fonctions se croisent. Afin de démontrer mathématiquement ces observations, nous séparons l'étude en deux cas : R- (les nombres négatifs) et R+ (les nombres positifs). Pour les nombres négatifs, nous montrons que la fonction E-x² est strictement supérieure à la fonction E2x-1, en utilisant le fait que E2x-1 est négatif. Ainsi, il n'y a pas de solution à l'équation pour les nombres négatifs. Ensuite, pour les nombres positifs, nous étudions la fonction f2x = E-x² - E2x-1. Nous montrons que cette fonction est strictement décroissante sur l'intervalle [0, +∞] en utilisant les propriétés des fonctions exponentielles. Nous montrons également que la limite de f2x quand x tend vers +∞ est -∞. En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe une unique solution à l'équation pour les nombres positifs. En résumé, il n'y a pas de solution à l'équation pour les nombres négatifs, et il y a une unique solution pour les nombres positifs.

TVI et calculs costauds !

La fonction f(x) = 2/(e^x + e^(-x)) est étudiée. Premièrement, on remarque que la fonction est toujours strictement positive car elle est une somme d'exponentielles positives. Ainsi, on peut exclure le cas où la fonction serait égale à 0. Ensuite, on analyse graphiquement le nombre de solutions de l'équation f(x) = x. On trace la fonction et on observe qu'il y a une unique solution. Pour montrer que la fonction g définie comme g(x) = f(x) - x est décroissante, on cherche d'abord si elle peut être décomposée en une somme de fonctions décroissantes. Cependant, on constate que f(x) n'est ni strictement croissante ni strictement décroissante, ce qui complique l'analyse. On est donc obligé de passer par le calcul des dérivées. On dérive f(x) en utilisant une formule et en simplifiant, on obtient une expression à partir de laquelle on peut évaluer le signe de la dérivée. Après une simplification et l'observation d'une identité remarquable, on arrive à exprimer g'(x) comme une somme de termes dont on peut déterminer les signes. On remarque que g'(x) est toujours négatif, ce qui montre que g(x) est décroissante. En conclusion, on peut dresser un tableau de variation simplifié pour la fonction g : elle est décroissante, continue et admet un unique point d'intersection avec l'axe des abscisses. Le nombre de solutions de l'équation f(x) = x est donc égal à 1.

Dérivabilité avec valeur absolue ?

Dans cet exercice, nous devons démontrer que la fonction donnée est continue et dérivable sur R, à l'exception du point x=0. Tout d'abord, nous commençons par vérifier que la fonction est définie sur R. En effet, peu importe la valeur de x, 1+x est strictement différent de 0, ce qui nous permet d'avoir une définition valide de la fonction. De plus, nous savons que le quotient de deux fonctions continues donne une fonction continue. Pour démontrer la continuité de la fonction, nous utilisons une calculatrice pour tracer son graphique et constatons qu'elle semble se rapprocher de 1 quand x tend vers l'infini et de -1 quand x tend vers moins l'infini. La fonction semble également relativement lisse, sans rupture de pente, ce qui soutient notre intuition de continuité. En ce qui concerne la dérivabilité de la fonction, nous supposons qu'elle est dérivable en x=0, car elle est clairement dérivable pour tous les autres points de R. En effet, x est dérivable sur R et 1+x en valeur absolue est dérivable partout sauf en 0. S'appuyant sur cette hypothèse, nous concluons que la fonction est dérivable sur tout R, à l'exception de x=0. Pour déterminer l'expression de la fonction en fonction du signe de x, cela est relativement simple. En vérifiant le comportement de la fonction en x=0, nous constatons qu'elle est bien continue, ce qui confirme notre expression. Enfin, pour justifier que la fonction est dérivable partout, sauf en x=0, nous utilisons le fait que x est dérivable et que le quotient de deux fonctions dérivables donne une fonction dérivable. Nous effectuons les calculs nécessaires pour dériver la fonction en x=0 et vérifions que le résultat est cohérent de chaque côté de ce point. Nous constatons que les dérivées de chaque côté de x=0 sont égales à 1, confirmant ainsi la dérivabilité de la fonction. En conclusion, nous démontrons que la fonction donnée est continue sur R et dérivable partout, sauf en x=0.

Équation Tangente

Dans ce cours, nous abordons la méthode de détermination des équations de tangentes, qui est une étape importante dans l'étude des fonctions. Il est essentiel de maîtriser cette méthode car elle est souvent utilisée dans les exercices où l'on doit étudier les tangentes et la position relative de la courbe par rapport à la tangente. Dans le premier exercice, nous devons étudier une fonction f, qui est égale à x^2 + 3x + 1. On nous demande de calculer f'(2) et f(2). Nous trouvons que f(2) = 11 et f'(2) = 7. En utilisant la formule y = f'(A) * (x - A) + f(A), où A est égal à 2, nous obtenons l'équation de la tangente, qui est y = 7x + 3. Ensuite, nous approfondissons la formule utilisée pour déterminer l'équation de la tangente. Nous démontrons que cette formule est simplement une équation de droite, y = mx + p, où m est le coefficient directeur et p est l'ordonnée à l'origine. En utilisant la connaissance de la tangente au point A, nous pouvons déduire que m = f'(A). Ensuite, en utilisant les coordonnées du point A, nous pouvons trouver p = f(A) - Af'(A). En regroupant ces résultats, nous obtenons l'équation de la tangente. Dans le deuxième exercice, nous devons étudier une nouvelle fonction g, qui est égale à e^x. On nous demande de trouver l'équation de la tangente à la courbe de g au point tapis 0. En calculant g'(0) = 1 et g(0) = 1, nous trouvons que l'équation de la tangente est y = x + 1. Il est important de bien maîtriser cette méthode car elle est fréquemment utilisée lors de l'étude des fonctions.

Formules Classiques

La dérivation est un rappel important en mathématiques. Il est essentiel de connaître parfaitement les formules de dérivation pour éviter des erreurs qui peuvent avoir un impact négatif sur les résultats d'un contrôle ou d'un examen. Il est donc crucial de s'assurer de la maîtrise de ces formules. Quelques exemples sont donnés pour illustrer l'utilisation des formules de dérivation. La dérivée de la fonction f(x) = 5x³ est 15x². Pour la fonction g(x) = (x^n)√(x), la dérivée est (n+1)x^(n-1) + (2/n)√(x). Pour la fonction h(x) = 1/v, la dérivée est -v'(x)/v², où v'(x) est la dérivée de v(x). Ensuite, l'utilisation des formules de dérivation est expliquée pour les cas du produit (u v) et du quotient (u/v). Pour le produit, la dérivée est u'v + uv'. Pour le quotient, la dérivée est (u'v - uv')/v². Des conseils méthodologiques sont donnés pour simplifier les calculs lors de la dérivation. Par exemple, le regroupement des termes de même degré est recommandé pour éviter des erreurs. Il est également utile d'utiliser des codes de couleur ou tout autre système de repérage pour faciliter la lecture et éviter d'oublier des termes importants. En conclusion, il est crucial de maîtriser les formules de dérivation et de les réviser régulièrement pour éviter des erreurs dans les calculs. Des méthodes méthodologiques, telles que le regroupement des termes de même degré, peuvent être utilisées pour éviter des oublis et des erreurs dans les calculs.

Polynômes 2nd Degré

Dans ce cours, on s'intéresse à l'étude d'un polynôme de degré 2. On cherche à aller plus vite que lors d'une étude classique de fonction. On commence par justifier l'ensemble de dérivabilité du polynôme, puis on calcule sa dérivée en utilisant les formules usuelles. On factorise si possible pour faciliter l'étude du signe de la dérivée. Ensuite, on déduit le tableau de variation en déterminant quand la dérivée change de signe. On calcule ensuite l'image au niveau de l'extremum qui est atteint en -b/2a. On sait déjà comment se comporte un polynôme de degré 2 grâce à la forme générale ax²+bx+c. Si a est positif, la courbe est en forme de "u" avec un minimum, et si a est négatif, la courbe est en forme de "n" avec un maximum. On peut utiliser ces informations pour aller plus vite dans l'étude du polynôme. On peut également utiliser les résultats classiques sur les polynômes de degré 2 pour trouver les coordonnées de l'extremum, l'ordonnée de l'extremum (-delta/4a), et les racines (-b+racine(delta)/2a et -b-racine(delta)/2a). Il est également important de remarquer que le minimum est au centre du polynôme et que les racines sont situées à égale distance du centre. Cette astuce permet de rapidement retrouver les résultats et de déduire le sens de variation et le signe de la fonction.

Étude f : Niveau MPSI mais outils de première !

Ce cours porte sur l'étude d'une famille de fonctions, notées f1, f2, etc., définies par f(x) = E(2x) / (x^n), où n est un entier naturel non nul. Le cours commence par déterminer le plus grand ensemble de définition de f, en excluant les valeurs de x pour lesquelles le dénominateur est nul. Ensuite, il est expliqué que f est dérivable sur tout son ensemble de définition, à l'exception de la valeur 0. Ensuite, le cours se concentre sur le cas où n est pair. On utilise la règle du produit et le comportement des puissances paires pour déterminer les variations de f, et on dresse le tableau de variation de f. Ensuite, les limites de f sont calculées en l'infini et en 0, et complétées dans le tableau de variation. Si n est impair, le comportement de f est différent. Les variations de f sont étudiées en utilisant le même raisonnement, et les limites en l'infini et en 0 sont calculées et ajoutées au tableau de variation. Le cours souligne également que l'étude de cas est essentielle dans l'exercice, en notant que les calculs seraient beaucoup plus difficiles sans la distinction entre n pair et n impair.

Composition : Déf

Dans cette vidéo, l'auteur explique ce qu'est la composition de deux fonctions en utilisant des exemples concrets. Il commence par décomposer une fonction en plusieurs étapes, en partant de x. Il explique que chaque étape consiste en une transformation de la fonction précédente. Par exemple, pour la fonction racine de x² plus 7, il passe successivement de x à x², puis de x² à x² plus 7, et enfin à la racine de x² plus 7. Il explique que cela revient à composer la variable x par trois fonctions simples. Ensuite, l'auteur donne une définition théorique de la composition de fonctions. Il explique que si on a deux fonctions U et V, où U est définie sur un intervalle i et à valeur dans un intervalle j, et V est définie sur j et à valeur dans un intervalle k, alors la composition de U et V, notée VU, est définie comme V de U de x. Autrement dit, on applique d'abord U à x, puis V au résultat obtenu. L'auteur mentionne également quelques propriétés de la composition de fonctions. Il explique que la composition de fonctions est associative, c'est-à-dire que (UV)W est égal à U(VW). Cependant, il précise que la composition de fonctions n'est pas commutative, c'est-à-dire que VU est généralement différent de UV. Pour illustrer cela, il donne l'exemple de deux fonctions U et V, où U est la fonction x² moins 7 et V est la fonction exponentielle. Il montre que VU et UV donnent des résultats différents, en prenant la valeur en 0 comme exemple. L'auteur conclut en rappelant l'importance de se rappeler que la composition de fonctions n'est pas commutative. Il encourage les spectateurs à poser des questions s'ils en ont, et les invite à se retrouver sur le forum pour discuter.

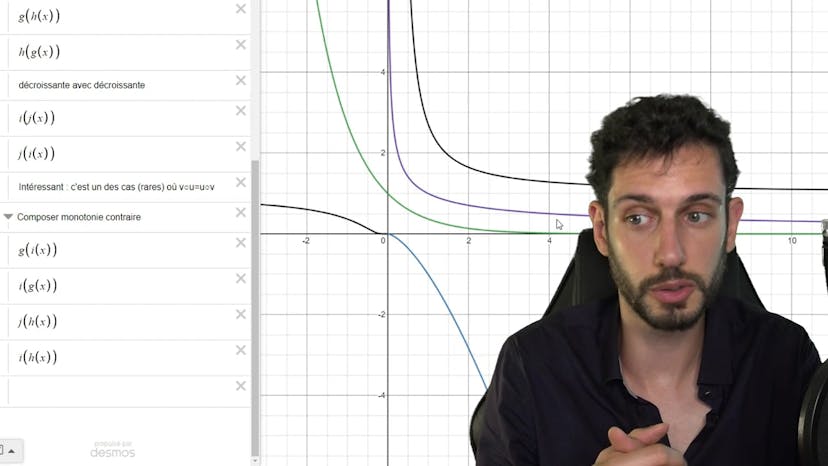
Dériver une composée

Dans cette vidéo, nous apprenons comment dériver une fonction composée. Nous commençons par expliquer ce qu'est la composition et les contraintes liées aux ensembles d'arrivée et de départ des fonctions composées. Ensuite, nous abordons les exemples les plus simples pour mieux comprendre le sujet. Par exemple, nous étudions la dérivée de 1/x et constatons que 1/u' ne correspond pas à la bonne formule, mais plutôt à -u'/u^2. Nous poursuivons avec d'autres exemples tels que la dérivée de racine de x et montrons que la bonne formule est (u'/2√u). Nous rappelons également les formules de dérivées de base, en insistant sur le fait qu'il faut toujours multiplier par u' lorsqu'il s'agit d'une fonction composée. Ensuite, nous donnons une définition formelle de la dérivée d'une fonction composée en utilisant les dérivées des fonctions u et v et en n'oubliant pas de multiplier par u'. Nous soulignons également qu'une conséquence intéressante est que si u et v ont la même monotonie, alors la fonction composée v∘u est croissante, tandis que si elles ont des monotonies contraires, la fonction composée est décroissante. Enfin, nous illustrons ces concepts avec des exemples concrets et montrons comment la monotonie des fonctions u et v affecte la monotonie de la fonction composée.

Fonction Composée

Dans ce cours, nous étudions une fonction composée et comment faire l'étude et le tableau de variation d'une fonction qui est composée de deux autres fonctions. Dans cet exemple, la fonction proposée est E2-1 sur x². Nous identifions les fonctions composantes de la fonction, g et h. La fonction g est -1 sur x², définie et dérivable sur R, tandis que la fonction h est l'exponentielle, définie et dérivable sur R. Nous utilisons les formules de dérivation pour trouver la dérivée de g, qui est 2 sur x³. Nous déterminons les variations de g en utilisant le signe de sa dérivée. Ainsi, on obtient un tableau de variation de g, qui est décroissante de moins l'infini à 0 et croissante de 0 à plus l'infini. Nous calculons également les limites de la fonction g, qui sont 0 en moins l'infini et moins l'infini en 0+. Ensuite, nous analysons la fonction h, qui est croissante sur R. En combinant les sens de variation de g et h, nous pouvons déduire les variations de la fonction composée, F. F sera donc décroissante sur R étoile moins et croissante sur R étoile plus. Nous calculons également les limites de F en utilisant les limites des fonctions composantes. La limite de F en moins l'infini est 1 et en plus l'infini est également 1. En 0, la limite de F est 0. Enfin, nous construisons le tableau de variation de F, qui est décroissante de 1 à 0 et croissante de 0 à 1. La fonction n'est pas définie en 0, mais peut être prolongée par continuité en posant F de 0 égale à 0. Une autre méthode aurait été de calculer directement la dérivée de F, mais nous avons choisi ici d'étudier l'intérieur de la composition. Si vous avez des questions, n'hésitez pas à les poser sur la FAQ.