Cours d'apprentissage en ligne

Propriétés 1 : intuitives !

Dans cette vidéo, nous abordons les propriétés basiques et intuitives de l'intégrale. La première propriété concerne la linéarité. Si nous prenons l'aire sous la courbe d'une fonction f, nous pouvons la multiplier par un coefficient lambda pour obtenir l'aire sous la courbe de la fonction lambda*f. Par exemple, si nous prenons l'aire sous la courbe x, puis l'aire sous la courbe 2x, nous aurons deux fois plus d'aire. La deuxième propriété concerne la somme de deux fonctions. Si nous cumulons les aires des fonctions f et g, nous obtiendrons l'aire totale de la fonction f+g. Cela signifie que l'aire totale est égale à l'aire de f plus l'aire de g. En ce qui concerne les bornes, si f est une fonction continue sur un intervalle [a,b], alors l'intégrale de f entre a et a est égale à zéro. Cela est dû au fait que nous prenons l'aire sous la courbe d'un point a à lui-même, ce qui représente un fil sans dimension. Par convention, si nous prenons l'intégrale de f entre b et a, cela sera équivalent à l'inverse de l'intégrale de f entre a et b. Donc, si nous parcourons la fonction de b à a, nous plaçons un signe négatif devant l'intégrale. Enfin, la relation de Schall indique que si nous additionnons l'intégrale de f entre a et c et l'intégrale de f entre c et b, nous obtiendrons l'intégrale de f entre a et b directement. Cela signifie que l'aire totale est égale à l'aire sous la courbe entre a et b, peu importe le point c choisi. Ces propriétés intuitives de l'intégrale sont importantes à comprendre. J'espère qu'elles sont claires pour vous et je vous retrouve bientôt pour d'autres vidéos sur les propriétés de l'intégrale. À tout de suite !

Propriétés 2 : remarques pratiques

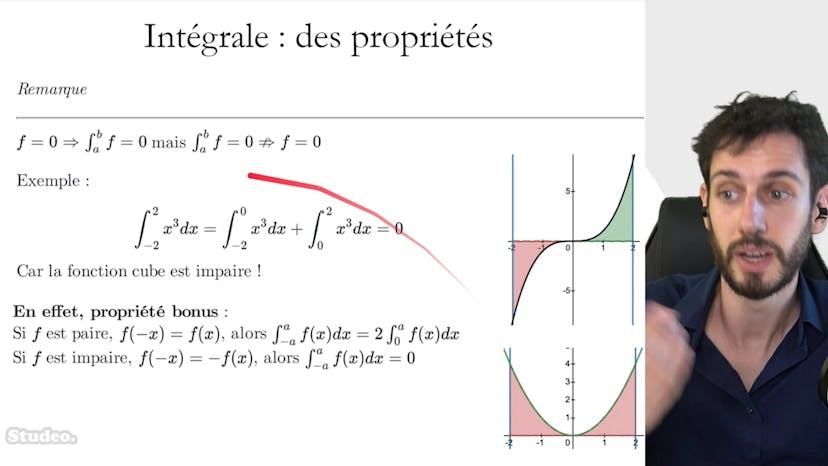
Résumé : Ce cours aborde plusieurs propriétés liées aux fonctions. La première propriété explique que si une fonction est nulle, alors son intégrale sur un intervalle donné sera également nulle. Cependant, il faut faire attention car une fonction dont l'intégrale est nulle ne sera pas forcément la fonction nulle. Une fonction peut avoir une intégrale nulle sur un intervalle donné, tout en ayant une valeur différente de zéro ailleurs. Ensuite, une deuxième propriété est présentée : si une fonction est paire, c'est-à-dire que pour tout x, f(-x) = f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera égale à deux fois l'intégrale de 0 à A. En revanche, si une fonction est impaire, c'est-à-dire que pour tout x, f(-x) = -f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera égale à 0. Enfin, la dernière propriété aborde les fonctions périodiques. Si une fonction est périodique avec une période T, alors l'intégrale sur un intervalle de taille T sera la même que celle sur un intervalle décalé de T. Cela signifie que l'intégrale entre A et A+T sera toujours égale à l'intégrale entre 0 et T. Ces propriétés sont très pratiques pour gagner du temps dans l'étude des fonctions et peuvent éviter des erreurs lors de résolution de problèmes.

Propriétés 3 : inégalités

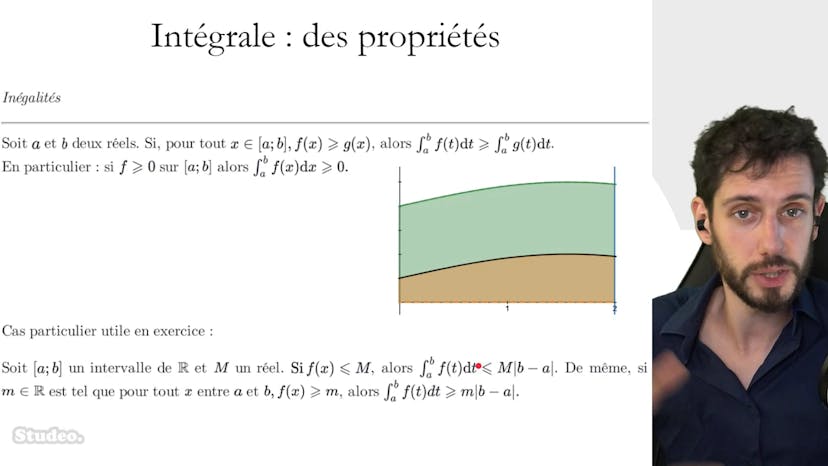
Dans cette courte vidéo, nous abordons les propriétés de l'intégrale liées aux inégalités. Si pour tout x appartenant à l'intervalle entre a et b, la fonction f(x) est toujours supérieure à la fonction g(x), alors les intégrales correspondantes seront également ordonnées de la même manière. En d'autres termes, l'intégrale de f sera plus grande que celle de g. Ce résultat peut être visualisé avec un dessin. Si f et g sont représentées graphiquement, l'aire sous la courbe de f sera beaucoup plus grande que celle de g. En particulier, si nous considérons le cas où g est la fonction nulle (c'est-à-dire que g(x) = 0 pour tout x), alors l'intégrale de f sera toujours positive. Cela peut sembler intuitif, mais il est important de connaître cette propriété. Une autre situation intéressante est lorsque f est inférieure à une fonction constante M. Dans ce cas, M est un majorant de f, ce qui signifie que f est bornée supérieurement. Dans ce contexte, l'intégrale de f entre a et b sera plus petite que l'intégrale de M entre a et b. L'intégrale de M est simplement l'aire d'un rectangle avec une base de longueur b-a (valeur absolue) et une hauteur M. De manière similaire, si f est supérieure à une constante M (c'est-à-dire que f(x) > M pour tout x), alors l'intégrale de f sera plus grande que l'aire du rectangle en dessous, c'est-à-dire M multiplié par la longueur de l'intervalle (b-a en valeur absolue). Ces propriétés sont simples mais importantes à connaître. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires. Je vous retrouverai dans la prochaine vidéo.

Théorème fondamental : Démo

Dans cette vidéo, nous démontrons le théorème fondamental de l'analyse, qui nous permet de comprendre intuitivement le théorème fondamental. Le théorème affirme que si f est une fonction continue et positive sur un intervalle [a, b], alors la fonction F définie comme l'intégrale de f entre a et x est dérivable et a pour dérivée f. Nous commençons par rappeler la définition de F(x) comme étant l'intégrale de f entre a et x. Nous remarquons également que F(a) est l'intégrale de f entre a et a, ce qui est nul car c'est l'intégrale d'une fonction sur une largeur nulle. En utilisant cette définition, nous démontrons que toute fonction continue sur un intervalle [a, b] possède des primitives sur cet intervalle. Cela découle du fait que toute fonction continue a au moins une primitive. Ensuite, nous entamons la démonstration directe du théorème fondamental. Pour montrer que F est dérivable en x, nous devons étudier la limite du taux d'accroissement. Nous souhaitons que cette limite soit égale à f(x). Nous prenons un x quelconque dans l'intervalle [a, b] et définissons le taux d'accroissement comme la limite lorsque h tend vers 0 de [F(x+h) - F(x)] / h. Nous simplifions cette expression en utilisant des propriétés des intégrales. Nous remarquons que l'intégrale entre x et a de f est égale à l'intégrale entre a et x lorsque nous échangeons les bornes d'intégration. 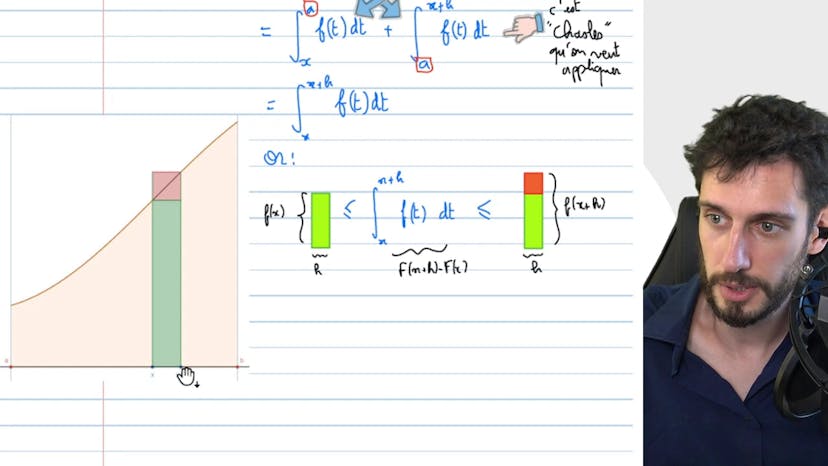Ensuite, nous utilisons la propriété de Schall pour dire que l'erreur entre x et x+h peut être remplacée par l'erreur entre x et a+h. Nous nous intéressons alors à cette erreur, que nous pouvons encadrer entre l'aire d'un rectangle vert et l'aire d'un rectangle bicolore composé du rectangle vert et d'une portion rouge. En calculant les aires de ces rectangles, nous obtenons une expression de F(x+h) - F(x) que nous pouvons diviser par h. Nous remarquons alors que cette expression est encadrée par f(x) et f(x+h). Comme f est une fonction continue, nous pouvons affirmer que la limite de f(x+h) lorsque h tend vers 0 est égale à f(x). Ainsi, nous avons démontré que le taux d'accroissement de F en x a pour limite f(x), ce qui prouve que F est dérivable et a pour dérivée f. En conclusion, cette démonstration du théorème fondamental de l'analyse nous montre que toute fonction continue et positive sur un intervalle possède des primitives sur cet intervalle. Cette démonstration utilise des propriétés des intégrales, l'approximation par des rectangles et le théorème d'encadrement pour arriver à cette conclusion.

Calcul d'Intégrale avec Primitive

Ce cours porte sur la méthode du calcul intégral et explique comment calculer une intégrale en utilisant une primitive. Trouver une primitive peut être difficile, mais c'est l'enjeu principal de ce chapitre. Dans l'exemple donné, l'intégrale à calculer est celle de x² moins cos2x de 0 à pi. Pour résoudre cette intégrale, il faut d'abord trouver la primitive de chaque terme de la somme. La primitive de x² est x³ et la primitive de cos2x est ½ sin2x. En appliquant le théorème fondamental, on obtient que l'intégrale de 0 à pi de f2x dx est égale à f2x en pi moins f0, ce qui donne pi³/3. Il est important de faire attention aux signes lors de l'application du théorème fondamental, il est recommandé d'écrire les moins avec des parenthèses pour éviter les erreurs. En développant les calculs, on peut obtenir plus facilement le résultat final, qui est pi³/3 dans cet exemple.

Fonction définie par une Intégrale

Le cours porte sur l'étude des variations d'une fonction définie par une intégrale. L'approche habituelle consiste à calculer la dérivée pour déterminer le signe de cette dérivée, puis en déduire la monotonie de la fonction. Cependant, la particularité ici est que la dérivée d'une intégrale est facile à calculer. L'exemple étudié concerne la fonction f définie sur l'intervalle [0, π] et égale à l'intégrale de 0 à x de sin^3(t). L'auteur met en garde contre une erreur souvent commise consistant à considérer que la dérivée est simplement sin^3. En réalité, cela dépend des bornes de l'intégrale. Pour illustrer cela, il donne un exemple de l'intégrale de -x à 0 de h(t) dt, où h est une fonction arbitraire. L'application du théorème fondamental de l'analyse permet de corriger cette erreur et de calculer la dérivée correcte. Ensuite, l'auteur effectue le calcul de la dérivée de la fonction f en posant g(t) = sin^3(t). En appliquant à nouveau le théorème fondamental, il obtient f(x) = g(x) - g(0) = sin^3(x). Ainsi, la fonction f est simplement égale à sin^3(x). Il souligne également l'importance de différencier les variables utilisées dans l'intégrale et dans l'expression globale de la fonction. La variable t n'a de sens que dans l'intégrale, elle n'est pas utilisée en dehors. La variable x, en revanche, est utilisée dans l'expression globale de la fonction. 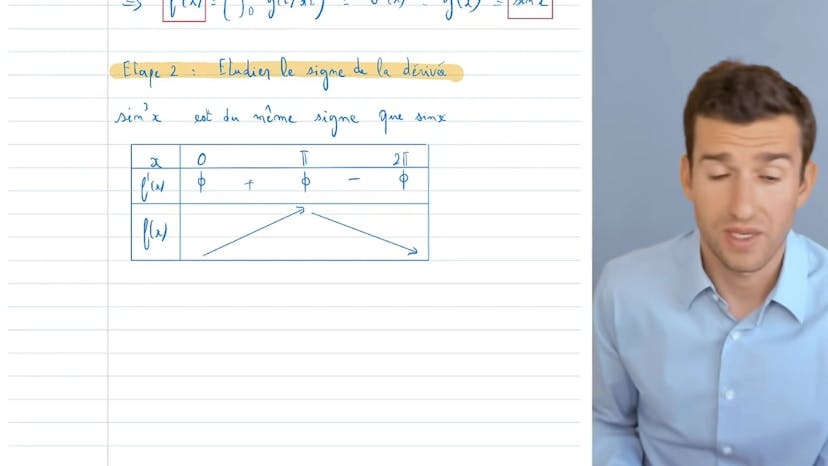Enfin, l'auteur analyse les variations de la fonction f en étudiant le signe de sa dérivée sin^3(x). Puisqu'il s'agit d'un cube, elle a le même signe que le sinus x sur l'intervalle [0, π]. Il conclut que la fonction f est croissante puis décroissante sur cet intervalle. En résumé, le cours explique comment étudier les variations d'une fonction définie par une intégrale. Il met en garde contre les erreurs fréquentes et donne des exemples concrets pour illustrer les méthodes de calcul.

Linéarité d'une Intégrale

Dans cette transcription vidéo, on étudie une méthode utilisant la linéarité de l'intégrale pour simplifier le calcul des primitives. On nous demande tout d'abord de montrer que la fonction F proposée est une primitive. Il suffit de dériver la fonction et de vérifier sa dérivabilité sur R, ce qui est assez simple car il s'agit d'un polynôme multiplié par une exponentielle. On obtient donc F de x en dérivant. Donc F est bien une primitive de la fonction donnée. Ensuite, on nous demande de déterminer l'intégrale de 0 à 1 de 3x moins 2 E de x. Il y a une erreur dans l'énoncé de la question, car "t" est utilisé au lieu de "x". La vraie intégrale que nous voulons calculer est donc 3x moins 2 fois E de x. Dans ce cas, la règle à garder en tête est que lorsqu'un polynôme est multiplié par une exponentielle, on utilise systématiquement une IPP (intégration par parties), car l'objectif est de réduire le degré du polynôme. Nous posons U de x égal à 3x moins 2, et sa dérivée est 3. Nous posons V égal à E de x, car la dérivée de V est également E de x. Nous avons donc les conditions nécessaires pour appliquer l'IPP. La dérivée de V est facile à primitiver car il s'agit de l'exponentielle. En utilisant l'IPP, nous obtenons une expression pouvant être calculée rapidement. Ensuite, nous avons l'intégrale de 0 à 1 de 3E2x, ce qui est beaucoup plus simple à calculer. Nous pouvons sortir le 3 et il nous reste seulement à intégrer E2x. La primitive de cette fonction est également E2x, donc nous obtenons E2x entre 0 et 1. En effectuant le calcul, nous obtenons 2E5. Pour résumer, lorsque nous avons un polynôme multiplié par une exponentielle, nous devons utiliser l'IPP. Dans cet exemple, nous avons utilisé cette méthode pour calculer facilement une intégrale. Si vous avez des questions, n'hésitez pas à les poser dans la faculté.

Encadrer une Intégrale

Dans ce cours, nous apprenons à encadrer des intégrales pour trouver des limites. Nous commençons par étudier une fonction f(x) égale à e^(-x^2). Nous voulons trouver l'encadrement de cette fonction pour tout x supérieur à 1. Nous remarquons que cette fonction est toujours positive car les exponentielles sont toujours positives. Ensuite, pour montrer que f(x) est inférieure à e^(-x), nous multiplions x (qui est supérieur à 1) par -1 pour changer le signe. Ainsi, nous obtenons -x^2 < -x. En composant cette inégalité avec l'exponentielle, nous voyons que f(x) est bien inférieure à e^(-x). En utilisant la propriété de monotonie de l'intégrale, nous pouvons donc encadrer l'intégrale de 1 à 2 de f(x) dx entre 0 et e^(-1) - e^(-2). Ainsi, nous avons résumé comment encadrer une intégrale en utilisant la monotonie de l'intégrale.

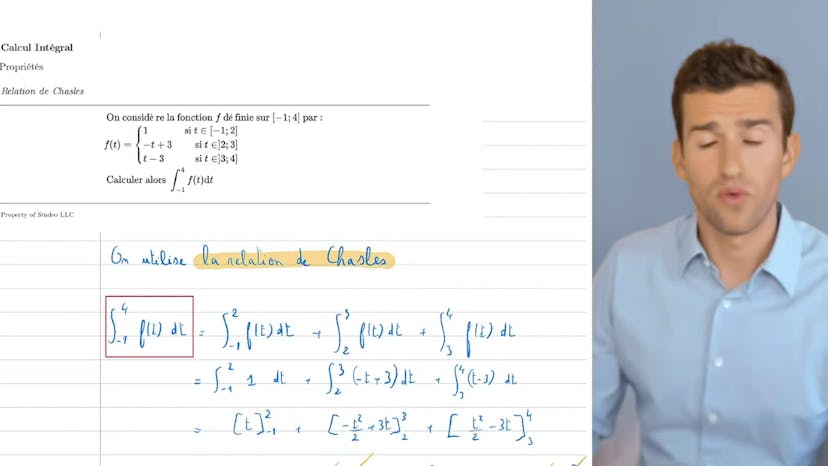
Relation de Chasles

Dans ce cours, nous apprenons comment utiliser la relation de Schall pour calculer une intégrale. La relation de Schall est simple à utiliser. Nous examinons une fonction f qui a différentes expressions selon l'intervalle. Elle est égale à 1 entre -1 et 2, elle est égale à -t+3 entre 2 et 3, et elle est égale à t-3 entre 3 et 4. Nous sommes ensuite invités à calculer l'intégrale de -1 à 4. Pour cela, nous utilisons la relation de Schall. Nous divisons l'intégrale en trois parties : de -1 à 2, de 2 à 3, et de 3 à 4. Nous utilisons les expressions correspondantes pour chaque partie, qui sont des fonctions courantes et faciles à intégrer. Nous effectuons les calculs et obtenons 5 comme résultat final. La relation de Schall nous permet de découper l'intégrale en plusieurs morceaux selon nos besoins. Il est important de faire attention à ce que les chiffres correspondent entre les différentes parties afin d'obtenir un résultat cohérent. Le point de départ doit être -1 et le point d'arrivée doit être 4, mais nous sommes libres de choisir le chemin que nous empruntons pour effectuer les calculs. En conclusion, la méthode de la relation de Schall est facile à appliquer si nous faisons attention aux détails et respectons les conditions de départ et d'arrivée.

Introduction

Ce cours est une introduction au nouveau sous-chapitre sur les intégrales, les applications et calculs. Le premier point abordé est l'utilisation des méthodes d'intégration pour calculer des primitives plus complexes, telles que l'intégration par parties. Ensuite, il est possible de calculer des aires entre des courbes en utilisant le lien établi entre les aires et les primitives dans le sous-chapitre précédent. De plus, la définition de la valeur moyenne d'une fonction est présentée, avec différentes méthodes associées. En résumé, ce cours aborde le calcul des aires sous une courbe, entre deux courbes, la valeur moyenne d'une fonction, ainsi que les méthodes d'intégration par parties. La partie la plus intéressante est l'accumulation d'exercices et de méthodes plus difficiles pour explorer les limites des calculs d'intégration par parties et d'aires. Bon courage pour cette partie et n'hésitez pas à consulter la FAQ en cas de questions ou de doutes. À bientôt pour la prochaine vidéo.

Intégration par Parties

Dans cette vidéo, nous abordons le thème de l'intégration par parties en mathématiques. L'intégration par parties est une formule qui permet de calculer des intégrales plus complexes. La formule de l'intégration par parties est la suivante : l'intégrale de uv' est égale à la primitive de uv moins l'intégrale de u'v. L'intégration par parties est ut