Cours d'apprentissage en ligne

Forme indéterminée 2 : la quantité conjuguée

Dans ce cours, nous étudions les méthodes pour les fonctions rationnelles, qui sont des polynômes divisés par d'autres polynômes. La technique utilisée est similaire à celle utilisée pour les polynômes eux-mêmes, c'est-à-dire que l'on factorise le terme de plus haut degré. Par exemple, dans l'exemple donné, nous étudions la suite Vn = 4n² / (n+1), qui est une fonction rationnelle. Nous identifions le terme de plus haut degré, qui est de degré 2, et nous factorisons par n². En bas, le degré est de 1, donc nous factorisons par n. Les n se simplifient ensuite partiellement, et nous obtenons 4n au numérateur divisé par 1 + 1/n qui tend vers 1. Ainsi, nous éliminons l'indétermination et nous voyons que la limite tend vers l'infini. En conclusion, Vn tend vers l'infini. Ensuite, nous étudions les différents cas de figure pour les fonctions rationnelles. Il y a trois cas possibles : soit le degré de P (le numérateur) est strictement supérieur au degré de Q (le dénominateur) ; dans ce cas, P l'emporte et la limite tend vers l'infini. Soit le degré de Q est strictement supérieur au degré de P ; dans ce cas, Q l'emporte et la limite tend vers 0. Le troisième cas est lorsque le degré de Q est égal au degré de P ; dans ce cas, les deux sont de même ordre de grandeur et la limite tend vers le rapport des coefficients dominants de Q et P. Par exemple, si nous prenons la suite Un = (3n² + 2n + 1) / (4n² + n + 4), nous factorisons par le terme de plus haut degré, n², et nous simplifions pour obtenir 3 + 2n + 1 / n² au numérateur, et 4 + 1/n + 4/n² en bas. Cette limite tend finalement vers 3/4, le rapport des coefficients dominants. En résumé, pour les fonctions rationnelles, nous avons toujours l'un des trois cas de figure mentionnés ci-dessus. Il est donc important de les prendre en compte lors de l'étude de ces fonctions.

Limite d'une somme géométrique

En résumé, ce cours explique que lorsqu'on a une somme à calculer, il est important de regarder les termes de la somme pour déterminer s'il s'agit d'une suite arithmétique, d'une suite géométrique ou autre. Dans ce cas précis, il s'agit de termes consécutifs d'une suite géométrique. En utilisant la formule appropriée, on peut calculer la somme en identifiant les valeurs des termes (u0=1, q=3) et en faisant attention au nombre de termes. La formule utilisée en l'occurrence est u0*(1-q^(nombre de termes))/(1-q). En simplifiant les calculs, on constate que la somme tend vers l'infini.

Trouver à la calculette "le plus petit entier tel que..."

Dans ce cours, nous étudions une suite et tentons de trouver le plus petit entier tel que la valeur de la suite soit supérieure à une certaine valeur. La suite est définie par la relation de récurrence un+1 = 3un, où u0 = 2. Nous pouvons voir que chaque terme de la suite est obtenu en multipliant le terme précédent par 3. Il est donc clair que les termes de la suite augmentent rapidement et tendent vers l'infini. En utilisant une calculatrice ou en effectuant de simples calculs, nous pouvons déduire que le sixième terme de la suite, u6, est supérieur à 1000. Par conséquent, le plus petit entier naturel tel que la valeur de la suite soit supérieure à 1000 est 6. En utilisant un programme simple, nous implémentons une boucle while qui continue tant que la valeur de u est inférieure à 1000. À chaque itération, la valeur de u est mise à jour en la multipliant par 3. Nous incrémentons également un compteur n à chaque itération pour suivre le nombre d'opérations effectuées. À la fin de la boucle, nous imprimons la valeur de n, qui correspond au rang de la suite où la valeur dépasse 1000. En résumé, il est important de comprendre la logique et l'objectif du programme. Dans ce cas, l'objectif était de déterminer le plus petit entier naturel tel que la valeur de la suite soit supérieure à 1000. Cela peut également être fait sans programme en itérant manuellement, mais l'approche programmée est plus rapide. N'hésitez pas à consulter la FAQ si vous avez des questions.

Test video

Aucun résumé n'est disponible pour cette vidéo

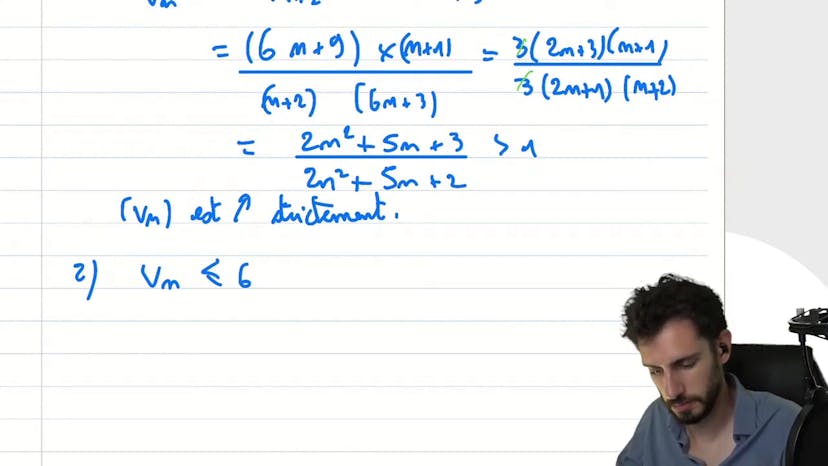
Fraction à transformer

Dans ce cours, on étudie une suite mathématique de la forme vn = 6n + 3 / (n + 1). Pour commencer, nous analysons ses variations en utilisant le critère de croissance qui compare vn+1 / vn avec 1. Nous montrons que ce ratio est supérieur à 1, ce qui signifie que la suite est strictement croissante. Ensuite, nous déterminons une borne supérieure pour la suite. En particulier, nous prouvons que vn est inférieur ou égal à 6 pour tout n. Ceci est établi en utilisant une équivalence logique qui simplifie l'expression de vn en ajoutant et en soustrayant 6. Enfin, nous appliquons le théorème de convergence monotone pour conclure que la suite vn converge. En effet, nous avons montré qu'elle est à la fois croissante et bornée, ce qui implique sa convergence. La limite de la suite vn est donc égale à 6.

Test

car cela ne fonctionne plus dans les dernières versions de l'application. Cependant, il est toujours possible de filmer l'écran et de capturer des images en attendant de résoudre ce problème. Je vais donc essayer d'expliquer les points importants de ce cours de manière SEO friendly. Dans cette vidéo, l'auteur fait un petit test pour évaluer les fonctionnalités de l'application. Il mentionne qu'il faut jeter une vidéo, ce qui signifie qu'il faut enregistrer une nouvelle vidéo. Il précise également que la durée de cette vidéo sera de quelques minutes. Ensuite, l'auteur évoque la possibilité de filmer l'écran, mais il n'est pas sûr de ce qu'il faut filmer exactement. Il parle également d'autres sujets plus anciens, sans donner plus de détails à ce propos. Il continue en disant qu'il y a du son et de l'image dans la vidéo, ce qui est intéressant. Après environ une minute, il annonce qu'il va maintenant passer à la révision, et il montre quelques flèches sur l'écran. Il mentionne également qu'il était endormi dans sa chambre. Au final, la durée de la vidéo est d'environ une minute et demie. L'auteur mentionne qu'il ne peut plus faire certaines choses, sans spécifier lesquelles. C'est tout ce que je peux résumer de ce cours en utilisant des termes SEO friendly.

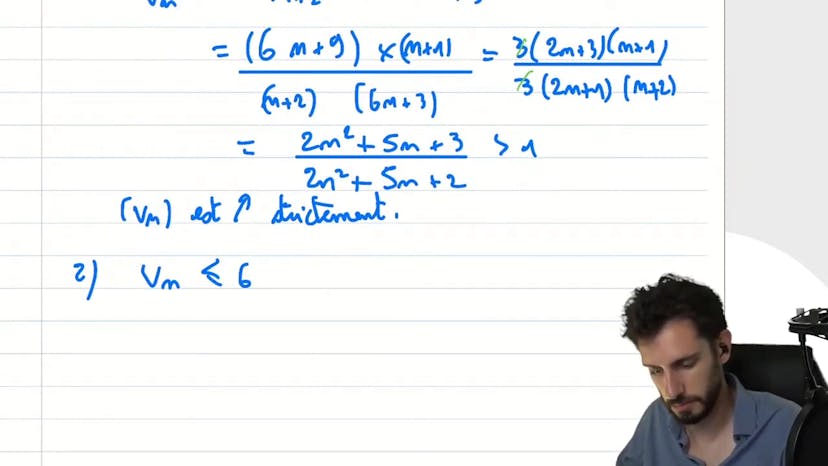
Suite-fraction

La suite vn est une suite définie par vn = 6n + 3 / n + 1. Pour étudier les variations de cette suite, on utilise le critère de croissance en calculant le ratio vn+1 / vn. On simplifie cette expression pour obtenir (2n² + 5n + 3) / (2n² + 5n + 2), qui est strictement supérieur à 1. Ainsi, on peut en déduire que la suite vn est croissante. Ensuite, on souhaite montrer que cette suite est majorée. On fait la supposition vn + 1 = 6 et on démontre par équivalence que cela est vrai si et seulement si 3 + 1 = 6, ce qui est effectivement vérifié. Donc, on peut affirmer que vn est majorée par 6. Enfin, on applique le théorème de convergence monotone qui stipule qu'une suite croissante et majorée converge. Ainsi, la suite vn converge vers une limite qui est 6. Une autre méthode pour étudier les variations de la suite vn consiste à simplifier son expression en écrivant vn = 6n + 3 / n + 1. En effectuant des calculs, on fait apparaitre l'expression 6n + 6 en haut et on compense cela en écrivant innocemment 6(n + 1) - 3. En séparant la fraction, on obtient f(n) = 6 - 3 / (n + 1), qui est une fonction croissante. Ainsi, on peut conclure que la suite vn est également croissante. De plus, en observant l'expression simplifiée de la suite vn, qui est 6 - 3 / (n + 1), on peut remarquer que lorsque n tend vers l'infini, le terme 3 / (n + 1) tend vers 0. Par conséquent, vn tend vers 6. En résumé, la suite vn = 6n + 3 / (n + 1) est croissante et majorée par 6, ce qui implique qu'elle converge vers la limite 6.

Plein de limites !

Pour ce deuxième exercice, nous allons aborder différentes méthodes de gestion des limites. Les deux principales méthodes que nous utiliserons sont la méthode du terme dominant et la méthode de l'encadrement. Dans la méthode du terme dominant, nous comparons les termes dominants en haut et en bas de la fraction. Par exemple, si nous avons une fraction avec 3n-8 au numérateur et 5n²-1 au dénominateur, nous pouvons dire que 3n-8 est négligeable par rapport à n² et que 5n²-1 est négligeable par rapport à n³ lorsque n devient très grand. Ainsi, nous pouvons simplifier la fraction en n²/n³, qui tend vers 1/2n et donc vers 0. La méthode de l'encadrement est utilisée lorsque nous avons des puissances négatives et des fonctions trigonométriques comme le cosinus et le sinus. Dans ce cas, nous encadrons ces termes entre -1 et 1. Par exemple, si nous avons une suite avec (-1)^n et le cosinus de n, nous pouvons dire que (-1)^n est compris entre -1 et 1, tout comme le cosinus de n. En utilisant un théorème d'encadrement, nous pouvons conclure que la suite tend vers plus l'infini. Il est également important de noter que lorsque nous avons des limites finies encadrées des deux côtés, nous pouvons utiliser le théorème des gendarmes pour conclure sur la convergence de la suite. En résumé, ces méthodes de gestion des limites, la méthode du terme dominant et la méthode de l'encadrement, simplifient le calcul des limites en nous donnant des indications sur le comportement des suites lorsque n tend vers l'infini. Il est essentiel d'encadrer les termes et d'utiliser les théorèmes de comparaison pour obtenir les résultats souhaités.

Téléscopage !

En résumé, ce cours aborde le sujet des limites de suites définies comme des sommes de termes d'autres suites. Le premier point consiste à déterminer la limite de la suite Un, qui est 1/n et tend vers 0. Ensuite, il faut montrer que pour toutes les valeurs appartenant à n étoiles, Un est égal à 1/n - 1/(n+1). Pour cela, il est conseillé de partir de cette expression et de simplifier jusqu'à obtenir Un. Ensuite, en utilisant la question précédente, on peut calculer la somme Sn. En utilisant une technique appelée somme télescopique, on peut simplifier les termes de la somme et il reste 1 - 1/(n+1). En concluant que la limite de Sn lorsque n tend vers l'infini est 1.

Majoration astucieuse

Le cours présente une méthode classique pour étudier les variations d'une suite et démontrer sa convergence. La suite en question est Vn = 6n + 3 / (n + 1). Pour déterminer les variations de la suite, on utilise le critère de croissance en comparant le ratio Vn+1/Vn à 1. On montre que ce ratio est supérieur à 1, ce qui signifie que la suite est strictement croissante. Ensuite, on démontre que la suite est majorée par 6 en montrant que Vn < 6 pour tout n. Enfin, on applique le théorème de convergence monotone pour conclure que la suite converge. On peut également utiliser une deuxième méthode pour étudier la suite en travaillant sur son expression. En utilisant des techniques de simplification, on obtient une expression équivalente de la suite et on montre ainsi qu'elle est croissante et bornée par 6. En utilisant les propriétés des limites, on conclut que la limite de la suite Vn est égale à 6.

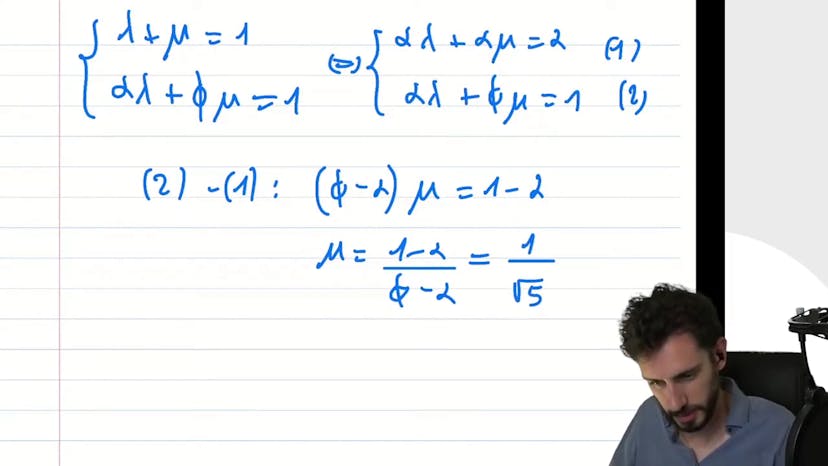
Prépa : Fibonacci

Le cours traite de la suite de Fibonacci et du nombre d'or. La suite de Fibonacci est définie par récurrence où chaque terme est la somme des deux précédents. On nous demande de trouver des réels a, b, lambda et mu tels que chaque terme peut être exprimé comme une combinaison linéaire de sommes géométriques. Plutôt que de traiter immédiatement les 4 inconnues, on cherche d'abord à déterminer s'il existe une seule somme géométrique qui vérifie la relation. On trouve deux possibilités a = (1 - √5)/2 et b = (1 + √5)/2, correspondant au nombre d'or. En utilisant ces valeurs, on résout un système d'équations pour trouver lambda et mu. Une fois que l'on a a, b, lambda et mu, on peut simplifier les calculs en utilisant les propriétés des suites géométriques. On peut ainsi déterminer que b^n tend vers b, qui est égal au nombre d'or. En utilisant cette information, on peut factoriser l'expression et conclure que le terme dominant tend vers 1. Au final, on trouve que la limite de la suite de Fibonacci divisée par le terme précédent tend vers le nombre d'or.