Cours d'apprentissage en ligne

Exo TRÈS classique

Dans cette méthode, on étudie une suite qui est une fonction rationnelle de n, où le degré du numérateur est égal au degré du dénominateur. La limite de cette suite est le quotient des coefficients dominants des polynômes constituant le numérateur et le dénominateur. On s'intéresse aux résultats préliminaires tels que la majoration, la croissance et la convergence. Dans le premier exercice, on considère la suite Un = (n-1)/(n+4) et on veut montrer qu'elle est majorée par 1. Pour cela, on remarque que le numérateur est plus petit que le dénominateur si c'est plus petit que 1. On peut alors partir de -1, dire que -1 est plus petit que 4, ajouter n, et ensuite faire le quotient. Comme c'est positif, le signe ne change pas, donc on en déduit que Un est strictement inférieur à 1. Pour étudier la monotonie de la suite, on utilise généralement Un+1 - Un. On peut parfois utiliser le quotient, mais il faut vérifier certaines conditions, comme le fait que Un ne s'annule jamais et qu'elle ne change pas de signe. Si la suite est constituée de produits de quotients ou de factoriels, on peut étudier le quotient Un+1/Un. Dans ce cas, on peut dire que la suite ne change pas de signe à partir d'un certain rang, car on s'intéresse à ce qui se passe à l'infini. On peut également utiliser la méthode du quotient Un+1/Un pour étudier les variations de la suite. On fait la différence entre deux quotients et on simplifie au maximum en développant. On peut alors observer les termes qui se suppriment. Si tous les termes restants sont positifs, on en déduit que la suite est strictement croissante. Si la suite est croissante et majorée, on peut conclure qu'elle est convergente. Cependant, la méthode du quotient ne permet pas de connaître la limite de la suite. Enfin, les exemples donnés dans le texte montrent qu'il est possible de trouver un majorant de la suite, mais cela ne garantit pas que la suite converge vers ce majorant. Il est important de faire attention à cela lors de l'utilisation des théorèmes de convergence.

Suite récurrente d'ordre 2

Dans cette méthode, on cherche les solutions complexes des suites récurrentes d'Ordre 2. On résout d'abord l'équation sans p2n, en utilisant l'équation de caractéristique. Les solutions sont de la forme lambda fois 2puissance n plus μ fois 3puissance n. Ensuite, on s'intéresse à la recherche d'une solution particulière avec p2n. On cherche une solution de la forme a fois 4puissance n, en résolvant l'équation. On obtient a égal à 1/2. Donc l'ensemble des solutions est la solution homogène plus la solution particulière, soit lambda fois 4puissance n plus mu fois moins 3 puissance n plus 4puissance n sur 2. Dans un autre cas, la valeur de p2n est n fois 2puissance n. On cherche une solution de la forme un polynôme fois 2puissance n, avec un degrés supérieur à la solution particulière précédente. On obtient a égal à 1/20 et b égal à moins 9/100. Donc l'ensemble des solutions est la solution homogène plus la solution particulière, soit lambda fois 2 puissance n plus mu fois moins 3 puissance n plus 40 fois n fois 2puissance n. Dans le dernier cas, on utilise le principe de superposition pour trouver la solution particulière. On ajoute les solutions particulières des deux cas précédents. On obtient la combinaison linéaire des solutions particulières, qui est égale à 3 quatorzième de 4 puissance n plus 40 fois n fois 2 puissance n. Voilà pour cette méthode sur les suites récurrentes d'Ordre 2.

Suite arithmético géométrique

Les suites arithmético-géométriques sont un cas particulier des suites définies par récurrence, où la relation de récurrence est donnée par u(n+1) = f(u(n)), avec f(x) = x + b (une fonction affine). Si a ≠ 1, alors la seule limite possible pour u(n) est l = b / (1 - a). Pour déterminer si la suite converge, on introduit une suite auxiliaire v(n) = u(n) - l, qu'on étudie ensuite. La suite v(n) est géométrique de raison a, et converge si |a| < 1. Ainsi, la suite u(n) converge si |a| < 1. Dans une application pratique, on considère un carré de côté 1, qu'on partage en 9 carrés et on colorie uniquement le carré central. On répète ensuite le processus en coloriant le carré central de chaque carré restant, et ainsi de suite. La relation de récurrence associée à cette géométrie est donnée par u(n+1) = (8/9)u(n) + (1/9)(1 - u(n)), où u(n) représente la proportion de la surface coloriée. En simplifiant cette relation, on obtient u(n+1) = (8/9)u(n) + (1/9). Comme a = 8/9, qui est compris entre 0 et 1 strictement, la suite u(n) converge vers 1. Ainsi, à chaque étape, une plus grande partie du carré est coloriée, et finalement, après un nombre infini d'étapes, tout le carré sera colorié.

Suites récurrentes

Les suites définies par récurrence sont des suites classiques en mathématiques. Elles se présentent sous la forme un+1 = f(un), où un est le terme de rang n de la suite. Pour étudier ces suites, on suit généralement une méthode en plusieurs étapes. Tout d'abord, on cherche à encadrer la suite, puis on examine sa variation. Ensuite, on détermine si la suite est convergente et on trouve sa limite. Dans cet exemple, on étudie une suite U définie par la relation un+1 = un/2 + un^2/4. On commence par l'encadrer en utilisant une méthode de récurrence, en montrant que la suite est comprise entre 0 et 1. Ensuite, on montre que la suite est décroissante en calculant la différence un+1 - un. Enfin, on conclut que la suite est convergente et on trouve sa limite en résolvant une équation du point fixe. Le processus général pour étudier les suites définies par récurrence est donc : encadrer la suite, examiner sa variation, déterminer si elle est convergente et trouver sa limite en résolvant l'équation du point fixe.

Suites complexes

Dans cette méthode, nous abordons les suites récurrentes d'Ordre 2 et leurs solutions complexes. Nous résolvons une équation de suite et recherchons des solutions complexes. Nous commençons par résoudre l'équation sans prendre en compte les p2n. Nous trouvons que les solutions sont de la forme lambda x 2puissance n plus mu x 3puissance n. Ensuite, nous étudions les solutions particulières avec p2n. Si p2n n'est pas l'une des deux solutions précédentes, nous cherchons une solution particulière sous la forme a x 4puissance n. En résolvant cette équation, nous trouvons la valeur de a et obtenons notre solution particulière. L'ensemble des solutions est alors la solution homogène plus la solution particulière. Dans le deuxième cas, si p2n est une solution simple de l'équation caractéristique, nous cherchons une solution de la forme un polynôme x 2puissance n avec un degré supérieur à celui de la solution particulière précédente. En résolvant cette équation, nous trouvons les valeurs de a et b et obtenons notre solution particulière. Encore une fois, l'ensemble des solutions est la solution homogène plus la solution particulière. Dans le dernier cas, nous utilisons le principe de superposition pour trouver la solution particulière en utilisant les solutions particulières des deux cas précédents. La solution particulière est alors la combinaison linéaire de ces deux solutions particulières.

Nombre d'or

Le sujet de ce cours est le nombre d'or, un nombre mathématique bien connu. La suite étudiée est définie de manière explicite, mais avec quelques points manquants. On cherchera le comportement de cette suite et on vérifiera si elle converge vers le nombre d'or. On démontrera également que la suite est croissante et on étudiera sa vitesse de convergence. On montrera que la suite converge vers le nombre d'or de manière très rapide, avec une vitesse de convergence du type 1 sur 2 puissance n. On conclura en soulignant l'importance de la vitesse de convergence lors des comparaisons et des équivalents.

Bolzano Weierstrass

Dans ce cours, nous abordons le concept de Bolzano-Weierstrass. Nous définissons une suite complexe avec une relation de récurrence et une suite auxiliaire. Nous essayons de montrer que la suite Mn est bornée et utilise l'inégalité ln pour bounded les valeurs. Ensuite, nous appliquons le théorème de Bolzano-Weierstrass pour montrer qu'il existe une fonction Phi telle que U de Phi converge. Enfin, nous démontrons que cela implique que la suite Un converge également grâce à une inégalité et le théorème d'encadrement.

Suite implicite

Le cours concerne les suites implicites, qui sont un peu plus compliquées que les suites explicites. La différence majeure est qu'au lieu d'avoir une relation de récurrence ou une expression explicite en fonction de n, on a une équation qui vérifie la suite. On étudie la suite en analysant son sens de croissance et sa convergence. L'exemple du cours concerne un polynôme Pn de x, qui est la somme des puissances de x jusqu'à x-1, avec un terme de -1. On doit montrer que Pn a une seule racine dans R+, notée Un, et que la suite Un est décroissante et donc converge. On utilise le Théorème des Valeurs Intermédiaires (TVI) pour montrer que Pn a une seule racine dans R+. On utilise également une inégalité entre les polynômes Pn et Pn+1 pour montrer que la suite Un est décroissante. On évalue Pn en 1/2 pour montrer que Un est supérieur ou égal à 1/2. Ensuite, on utilise une autre expression de Pn, une suite géométrique, pour montrer que la limite de Pn en Rho (un réel entre 1/2 et 1) est strictement positive. Enfin, on utilise cette information pour montrer que la suite Un tend vers 1/2 en utilisant la définition formelle de la limite.

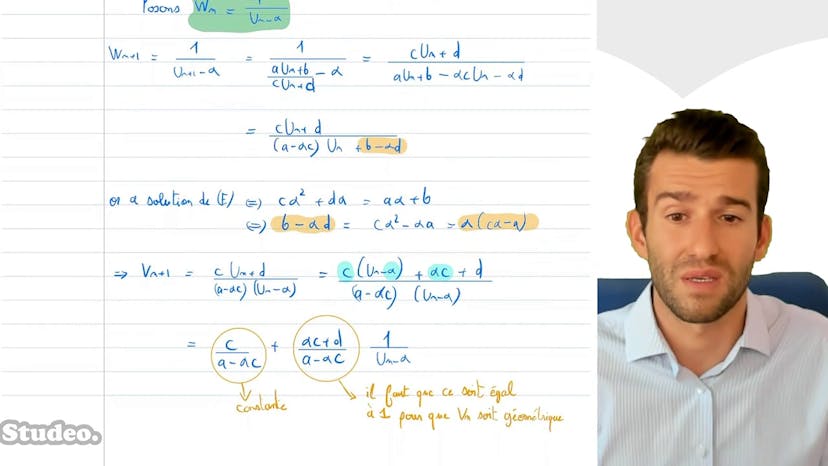
Suite homographique

Une suite homographique est une suite qui vérifie une relation de récurrence de la forme "un+1 = (aun + b)/(cun + d)". Il y a deux cas possibles : soit l'équation a deux solutions, auquel cas on pose une suite auxiliaire géométrique, soit elle a une seule solution, auquel cas on pose une suite auxiliaire arithmétique. En utilisant ces suites auxiliaires, on peut trouver l'expression de la suite homographique. Pour trouver l'expression de ces suites auxiliaires, on peut résoudre l'équation homographique et poser des suites auxiliaires en fonction des solutions trouvées. En utilisant différentes manipulations et simplifications, on peut obtenir l'expression de ces suites auxiliaires et remonter à l'expression de la suite homographique. En conclusion, les suites homographiques peuvent être résolues en posant des suites auxiliaires géométriques ou arithmétiques en fonction des solutions de l'équation homographique. Ces suites auxiliaires permettent de trouver l'expression de la suite homographique. Des exemples sont présentés pour illustrer le processus de résolution.

Encadrement

Dans ce cours, nous allons apprendre une astuce pour l'encadrement. Cette astuce est assez simple et rapide à utiliser, mais il est important de savoir la maîtriser car elle peut être utile dans certains exercices. La méthode consiste à utiliser deux suites de règles entre 0 et 1, telles que la limite entre un et vn en tant que produit tend vers 1. L'objectif est de démontrer que les suites un et vn convergent toutes les deux vers 1. Pour cela, nous allons prendre l'exemple de la suite un. Nous utilisons le fait que vn est compris entre 0 et 1, nous pouvons alors encadrer un en le limitant entre 1 et un-vn. En utilisant le théorème d'encadrement, nous concluons que un tend vers 1. Il est important de noter que cette astuce peut également être appliquée à la suite vn. Il s'agit donc d'une astuce rapide mais utile pour passer du produit de suite à l'une des deux suites. N'oubliez pas de bien maîtriser cette méthode car elle peut être fréquemment utilisée.

Suites adjacentes

Les suites adjacentes sont étudiées dans ce cours. Deux suites sont couplées et imbriquées l'une par rapport à l'autre. Une combinaison linéaire est utilisée pour simplifier le problème. On découvre que VN-UN est une suite géométrique de raison un tiers, avec un signe constant. On en déduit que UN et VN sont monotones et de sens de variation opposé. De plus, VN-UN tend vers zéro, ce qui montre que les deux suites sont adjacentes et convergent vers une limite commune L. En utilisant cette information, on obtient l'équation U0+V0=2L, ce qui permet de trouver la valeur de L. La subtilité est que cette fois-ci, c'est aux étudiants de trouver les combinaisons linéaires.