Cours d'apprentissage en ligne

Continuité en un point

Dans cette vidéo, Paul nous parle de la continuité de la fonction g définie sur R. La fonction g est définie comme suit : - g(x) = 1/|x| si x n'est pas égal à -1, 0 ou 1 - g(x) = 0 si x est égal à -1, 0 ou 1 Tout d'abord, on étudie la continuité de g sur R privé de -1, 0 et 1. On remarque que g ne s'annule pas sur R privé de -1, 0 et 1, donc la fonction x1 sur le diagramme de valeur absolue de x est continue sur -1, 0 et 1. Donc, g est continue sur R privé de -1, 0 et 1. Ensuite, on étudie la continuité de g en -1, 0 et 1. Pour cela, on calcule les limites de g lorsque x tend vers -1, 0 et 1. La limite de g(x) quand x tend vers 0 avec x différent de 0 est égale à la limite de 1/|x| quand x tend vers 0, et cette limite est égale à 0, qui est la valeur de g(0). Donc, g est continue en 0. Par contre, la limite de g(x) quand x tend vers 1 avec x différent de 1 est égale à la limite de 1/|x| quand x tend vers 1, et cette limite est égale à l'infini. Donc, g n'est pas continue en 1. De la même manière, g n'est pas continue en -1, car la limite de g(x) quand x tend vers -1 avec x différent de -1 est également infinie. Ainsi, on conclut que g est continue sur R privé de -1 et 1. C'est la fin de cet exercice, à bientôt pour une prochaine vidéo !

Continuité avec paramètres

Dans cette vidéo, Paul explique la continuité des fonctions. Il commence par étudier la continuité de la fonction f pour une valeur a donnée. Il décompose la fonction en plusieurs morceaux continus et vérifie qu'ils se raccordent correctement. Il conclut que la fonction f est continue si et seulement si a est égal à 0 ou 1. Ensuite, Paul examine la fonction g et cherche les valeurs des constantes α, β et γ pour lesquelles la fonction est continue. Il analyse les points de raccordement et utilise des équations pour déterminer les relations entre les constantes. Il trouve que f est continue si α + β = 1 et γ + β = 1. Il en déduit que α = γ et que β = 1 - γ. Ainsi, f est continue pour α, β, γ appartenant à l'ensemble (x, 1-x, x) pour x appartenant à R, où γ est libre et peut prendre n'importe quelle valeur réelle. En résumé, la vidéo explique les concepts de continuité des fonctions, examine la continuité de la fonction f pour différentes valeurs a, et détermine les valeurs des constantes α, β, γ pour lesquelles la fonction g est continue.

Prolongements par continuité de fonctions cosinus et sinus

Dans cette vidéo, nous étudions le prolongement par continuité de fonctions contenant des sinus et des cosinus. Nous commençons par examiner la fonction f2x = sin(x) * sin(1/x), qui n'est pas définie en 0 et -1. Nous constatons que sin(1/x) n'a pas de limite en 0, mais sin(x) est borné. Ainsi, f est continue sur l'intervalle réel positif, et f peut être prolongée par continuité en 0 en définissant f(x) = 0. Ensuite, nous examinons la fonction g(x) = cos(x) * cos(1/x). Nous avons déjà vu que cos(1/x) n'a pas de limite en 0, et en démontrant que les limites de deux suites u et v, qui tendent toutes deux vers 0, sont différentes lorsque nous les appliquons à g, nous concluons que g n'a pas de limite en 0. Par conséquent, g ne peut pas être prolongée par continuité en 0. Finalement, nous étudions la fonction h(x) = sin(x+1) * ln|1+x|. Nous examinons la limite de h(x) lorsque x tend vers -1 et constatons qu'elle est indéterminée. Pour résoudre cette indétermination, nous utilisons l'astuce de poser u = x+1, ce qui nous permet de réécrire h(x) en termes de sin(u) et ln|u|. Nous utilisons ensuite les connaissances sur les limites du sinus et du logarithme en 0 pour déterminer la limite de h(x) lorsque x tend vers -1. En utilisant la croissance comparée, nous concluons que la limite de h(x) est égale à 0. Par conséquent, h peut être prolongée par continuité sur l'ensemble des réels en définissant h(x) = 0 lorsque x = -1. Ceci conclut l'exercice sur les prolongements par continuité des fonctions avec des sinus et des cosinus à l'intérieur.

Indicatrice de Q

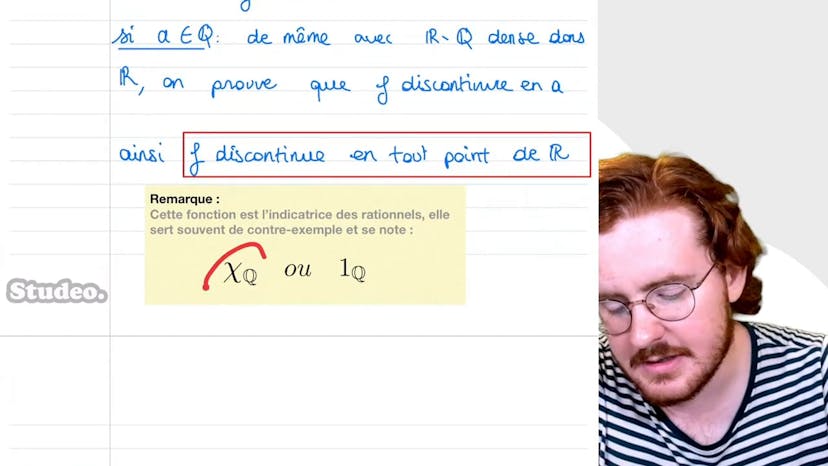
Dans ce cours, Paul aborde la fonction f de R dans R, qui est définie comme suit : f(x) = 1 si x est rationnel, et f(x) = 0 si x n'est pas rationnel. Cette fonction est appelée la fonction indicatrice des rationnels. Pour démontrer que f est discontinue en tout point, Paul explique qu'il suffit de visualiser la fonction. Comme les rationnels sont présents partout dans R, on peut imaginer deux droites qui se croisent en chaque point. Cependant, les points sont si proches les uns des autres qu'ils semblent alignés, donnant une impression de continuité. Cependant, la fonction alterne constamment entre 0 et 1 à chaque changement de rationnel à irrationnel, ce qui montre qu'elle n'est pas continue. Paul montre ensuite comment prouver la discontinuité de f en utilisant la caractérisation séquentielle de la continuité. Il explique qu'il suffit de trouver une suite de réels qui converge vers un point a donné, mais dont les images par f ne convergent pas vers f(a). En utilisant la densité de Q (les rationnels) dans R, Paul démontre que f est discontinue en a, que a soit un rationnel ou un irrationnel. Il conclut en précisant que cette fonction, qui est simple mais discontinue en tout point, est souvent utilisée comme un contre-exemple dans l'étude de la continuité. Elle est notée qui-q ou un-q, et est appelée l'indicatrice des irrationnels. C'est ainsi que se termine ce cours, avec une invitation à la prochaine fois.

Fonctions min et max

Dans cette vidéo, Paul explique comment prouver que les fonctions minimum et maximum de deux autres fonctions, f et g, sont également continues. Il commence par souligner qu'il existe différentes méthodes pour prouver la continuité d'une fonction, comme la définition traditionnelle ou l'utilisation de suites. Cependant, il affirme que la façon la plus rapide est d'utiliser des théorèmes généraux. Paul rappelle également qu'il est possible d'exprimer les fonctions minimum et maximum en fonction de f et g à l'aide de fonctions visuelles qui sont déjà connues pour être continues. Pas besoin de les redémontrer. Il explique ensuite comment exprimer le minimum et le maximum en termes de valeurs a et b dans R². Il fait remarquer que la somme du maximum et du minimum de a et b est égale à a + b. Ensuite, il explique qu'en utilisant la somme et la différence, on peut obtenir une expression pour le minimum et le maximum en utilisant demi-somme et demi-différence. Il note que le maximum de a et b et le minimum de a et b sont égaux à la distance entre a et b, qui est équivalente à la valeur absolue de a - b. Ainsi, il conclut que le maximum de f et g est égal à la somme de f et g, plus la valeur absolue de f - g, le tout divisé par 2. Et le minimum de f et g est égal à la somme de f et g, moins la valeur absolue de f - g, également divisé par 2. En utilisant ces expressions et les théorèmes généraux, il montre que les fonctions minimum et maximum de f et g sont continues en x0. Paul insiste sur l'importance de prendre du recul dans cet exercice et de ne pas se précipiter dans des démonstrations complexes. Il souligne qu'il faut réfléchir à l'astuce et aux connaissances sur les fonctions minimum et maximum. Faire un dessin peut également aider à visualiser les concepts. En conclusion, Paul affirme que les fonctions minimum et maximum de f et g sont continues en x0, et il encourage les spectateurs à réfléchir davantage avant de se lancer dans des démonstrations complexes.

Équation fonctionnelle

Dans cet exercice sur les fonctions continues, on cherche à résoudre une équation fonctionnelle. On souhaite trouver des fonctions f de R dans R qui vérifient f(x + y) = f(x) + f(y). Les fonctions linéaires, c'est-à-dire les fonctions f(x) = x, sont une réponse évidente. On peut également les décrire comme f(x) = f(1) * x. Cette dernière formulation peut être utile pour simplifier l'équation. On commence par remarquer que f(0) est égal à f(0), ce qui est facile à prouver et peut être utile. En généralisant, on peut montrer que f(nx) = nf(x) pour tout entier n. La preuve se fait par récurrence. On utilise ensuite la continuité et la densité des rationnels dans les réels pour étendre cette propriété aux rationnels. Plus précisément, on montre que pour tout x dans R et tout rationnel r = p/q, f(r * x) = r * f(x). On utilise alors la densité des rationnels et la continuité de f pour prouver que cette propriété s'étend à tous les réels. Ainsi, on démontre que si une fonction satisfait cette équation fonctionnelle, alors elle appartient à l'ensemble des fonctions linéaires, c'est-à-dire l'ensemble des fonctions de la forme f(x) = k * x. En conclusion, on a résolu l'équation fonctionnelle en trouvant toutes les fonctions continues f de R dans R qui vérifient f(x + y) = f(x) + f(y).

Variations et théorème des valeurs intermédiaires

Dans cet exercice, nous étudions le tableau de variation d'une fonction polynomiale G dont la dérivée est G'(x) = 6x² - 6x. Nous dressons le tableau en calculant les limites et en cherchant les extrêmes locaux de G. Ensuite, nous devons montrer qu'il existe une solution alpha telle que G(alpha) = 0, avec alpha étant encadré entre -1 et 10^-1. Nous utilisons le corollaire du théorème des valeurs intermédiaires pour montrer qu'il existe une unique solution alpha sur l'intervalle (1, +∞). Nous pouvons également encadrer alpha à l'aide d'une calculatrice. Nous déterminons ensuite le signe de G(x) pour tout x réel en utilisant le tableau de variation précédent. Ainsi, pour tout x appartenant à (-∞, alpha), G(x) est strictement inférieur ou égal à 0, et pour tout x appartenant à (alpha, +∞), G(x) est supérieur ou égal à 0. Enfin, nous étudions la fonction f définie par f(x) = (1-x)/(x³ + 1) et nous calculons f'(x) en exprimant cette dérivée en fonction de G(x). Nous remarquons que le numérateur de f'(x) correspond à G(x), ce qui nous permet de déduire le signe de f'(x). Nous concluons que f est décroissante sur (-1, alpha) et croissante sur (alpha, +∞). C'est ainsi que se termine cet exercice sur l'analyse de fonctions. Rendez-vous la prochaine fois !

Point fixe et continuité

Dans cet exercice, nous cherchons à prouver que la fonction F est continue et a un point fixe sur le segment AB. Pour prouver cela, nous représentons graphiquement F dans un carré délimité par les valeurs d'A et B. Nous montrons que même en essayant d'éviter la droite identité, le graphique de F finit par l'intersecter à certains points. Ensuite, nous introduisons la fonction G(X) = F(X) - X, qui nous permet de ramener le problème à trouver une solution à l'équation G(X) = 0. En utilisant le théorème des valeurs intermédiaires, nous démontrons que l'équation G(X) = 0 a au moins une solution sur le segment AB, ce qui signifie que F(X) = X a également au moins une solution sur ce segment. Ainsi, nous prouvons l'existence d'un point fixe pour F.

Fonction bornée

Dans cet exercice, nous étudions les fonctions continues sur un intervalle. La fonction f est définie sur R par f(x) égale à un polynôme de degrés pairs et une exponentielle de moins x carré. L'objectif est de démontrer que la fonction est bornée sur R. Pour y parvenir, nous devons déterminer les limites de f à l'infini et moins l'infini. En utilisant les règles de calcul avec les limites, nous trouvons que la limite du polynôme est c plus l'infini et la limite de l'exponentielle est c0 plus l'infini. Les limites sont les mêmes à moins l'infini. Selon les croissances comparées, l'exponentielle l'emporte toujours, donc les limites l'emportent sur le polynôme. Par conséquent, les limites en plus l'infini et moins l'infini de f sont 0. 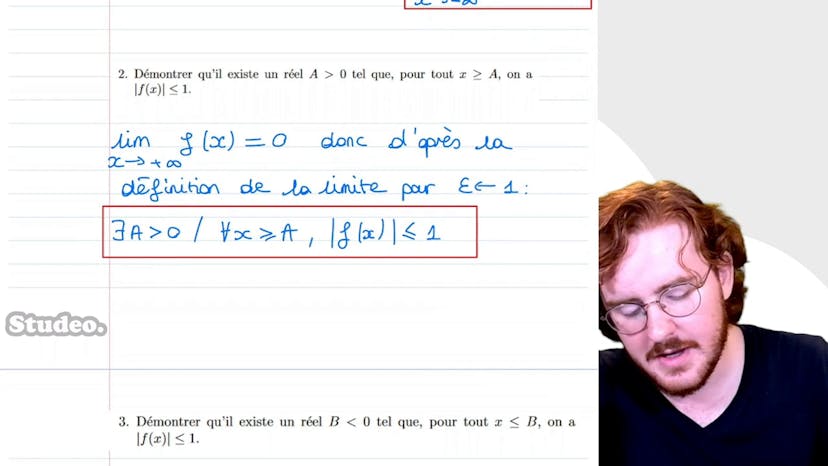Ensuite, nous démontrons qu'il existe un réel a strictement supérieur à 0 tel que pour tout x supérieur ou égal à a, la valeur absolue de f(2x) est inférieure ou égale à 1. Cela correspond à la définition de la limite lorsque ε reçoit 1. De manière similaire, nous démontrons qu'il existe un réel b strictement inférieur ou égal à 0 tel que pour tout x inférieur ou égal à b, la valeur absolue de f(2x) est inférieure ou égale à 1. Cette fois-ci, nous utilisons la définition de la limite en moins l'infini. En utilisant les résultats des questions précédentes, nous remarquons que la fonction f est bornée à chaque fois sur les intervalles moins l'infini à b et a à plus l'infini. Puisque f est également continue sur l'intervalle ab, nous pouvons appliquer le théorème des bornes atteintes, ce qui signifie que f est bornée sur cet intervalle et atteint ses bornes. Par conséquent, f est bornée sur R tout entier. Voilà, c'est la fin de cet exercice sur les fonctions continues sur un intervalle. À la prochaine fois !

Bijection réciproque

Dans ce cours, Paul aborde le lien entre continuité, bijection et la fonction f(x) = 1 + e^x. Il montre que f est une bijection de R sur son image en utilisant le théorème de la bijection. Pour cela, il prouve que f est continue et strictement croissante en utilisant la dérivée de f. Il conclut donc que f réalise une bijection de R sur son image. Ensuite, il détermine le domaine d'arrivée de f et la bijection réciproque en résolvant l'équation f(x) = y. Il trouve que le domaine d'arrivée est R+* et que la bijection réciproque de f est f^-1 (y) = ln(e^y - 1) pour tout y dans R+*.

Équivalent d'une bijection réciproque

Dans cette vidéo, nous étudions une fonction f définie comme f(x) = x-2 + log(x), où la fonction logarithme est définie sur l'ensemble des nombres réels positifs. Nous montrons tout d'abord que f réalise une bijection de l'ensemble des nombres réels positifs sur l'ensemble des nombres réels inclus dans R. Nous utilisons la forme explicite de f et montrons sa stricte monotonie et continuité pour prouver cette bijection. De plus, nous démontrons que l'application réciproque de f, appelée g, est également une bijection. En utilisant le théorème de limite monotone, nous déterminons les limites de g aux bornes de l'intervalle, c'est-à-dire à l'infini et moins l'infini. Nous appuyons notre démonstration sur le fait que g est strictement croissante et minorée par zéro. Nous prouvons ainsi que la limite de g à l'infini est plus l'infini et à moins l'infini est zéro. Ensuite, nous démontrons que l'équation f(x) = 0 admet une unique solution dans l'ensemble des nombres réels positifs, que nous notons alpha. Enfin, nous étudions la limite de f(x)/x et utilisons cette information pour déduire une limite pour f(g(t))/g(t) ainsi qu'un équivalent de g au voisinage de l'infini. Nous concluons la vidéo en résumant les résultats obtenus.