Cours d'apprentissage en ligne

Points d'Inflexion

Ce cours porte sur la convexité d'une fonction et la façon de déterminer les points d'inflexion. La fonction étudiée est f2x. Nous commençons par dériver cette fonction deux fois pour justifier sa dérivabilité. En calculant la dérivée, nous remarquons la présence d'une exponentielle toujours positive. Cependant, le signe de "-x plus 1" est important. Il est positif lorsque x tend vers moins l'infini jusqu'à 1, et négatif sinon. En déduisant le signe de la dérivée, nous obtenons un tableau de variation de la fonction f. Celle-ci est croissante puis décroissante avec un maximum atteint à 1, évalué à 7e moins 1. Les limites de la fonction sont également calculées, avec -∞ tendant vers 0 et +∞ tendant également vers 0 grâce à une comparaison de croissance. Ensuite, nous calculons la dérivée seconde de f(x) et trouvons 7 fois x moins 2 fois e de moins x. Comme l'exponentielle est toujours positive, le signe de f''(x) suit celui de x moins 2, positif pour x supérieur à 2 et négatif sinon. Ainsi, f''(x) change de signe en x=2, ce qui indique un point d'inflexion à ce point. Les coordonnées de ce point sont calculées et correspondent à f de 2 égal à 14 de 2 moins 2. En regardant la courbe de f, on observe que la pente diminue avant le point d'inflexion et augmente après, créant une courbe incurvée. La courbe de f'' est également tracée et montre que la dérivée seconde est d'abord négative avant de changer de signe en 2. Les points d'inflexion sont souvent rencontrés dans des problèmes de physique, tels que les titrages, où ils indiquent un changement de pente. Cette méthode sur la convexité et les points d'inflexion constitue la dernière partie de ces différentes méthodes étudiées.

Convexité étude COMPLETE

Aucun résumé n'est disponible pour cette vidéo

Fonctions cubes et convexité

Ce cours concerne l'étude de la convexité d'une fonction f(x) = Ax^3 + Bx^2 + Cx + D. L'exercice consiste à déterminer dans quels cas la fonction est convexe ou concave. Il s'agit d'un exercice plus avancé mais qui essaie de généraliser les résultats intuitifs sur les fonctions cubiques. On commence par calculer la dérivée seconde de f(x) et la dérivée de f(x). La convexité de f(x) dépendra du signe de la dérivée seconde (f''(x)) et donc de la valeur de A. Si A est positif, la fonction affine A*x + 2B est d'abord négative, puis positive. Donc f''(x) sera négative, puis positive. Dans ce cas, la fonction f(x) sera concave, puis convexe. Si A est négatif, la fonction affine A*x + 2B est d'abord positive, passe à 0, puis devient négative. Donc f''(x) sera positive, puis négative. Dans ce cas, la fonction f(x) sera convexe, puis concave. Il est important de faire attention à la distinction des cas et de comprendre le rôle de A dans les calculs. Si on ne tient pas compte du signe de A, on risque de faire des erreurs. De plus, on remarque que peu importe la valeur de A, la fonction admet un point d'inflexion à x = -B/(3A). Un point d'inflexion est un point où la courbe change de convexité. En appliquant ces résultats à un exemple précis, on peut conclure que la fonction f(x) = -x^3 + 2x^2 + 3x - 4 admet un point d'inflexion à x = 4/3. En résumé, cet exercice permet de comprendre la convexité d'une fonction cubique en fonction de la valeur du coefficient A. Il met l'accent sur la distinction des cas et l'utilisation des dérivées pour déterminer la convexité.

Des inégalités classiques

Dans cet exercice, on utilise la convexité et la concavité pour démontrer certaines inégalités. Tout d'abord, on démontre que pour tout réel X, l'exponentielle de X est supérieure à 1 + X, et même si X est non nul, l'inégalité est stricte. Pour cela, on remarque que 1 + X peut être vu comme l'exponentielle de 0 fois X + l'exponentielle de 0. On reconnaît alors l'équation de la tangente à la courbe de l'exponentielle de X au point (0,1). Comme l'exponentielle de X est strictement convexe, la courbe est au-dessus de cette tangente, et donc E(X) est supérieur ou égal à 1 + X pour tout X réel. Si X est différent de 0, alors E(X) est strictement plus grand que 1 + X. Ensuite, on démontre que le logarithme de (1 + X) est inférieur ou égal à X. On remarque que le coefficient directeur de la tangente à la courbe de log(1 + X) en 0 est 1, donc la dérivée de log(1 + X) est égale à 1 / (1 + X), et elle vaut 1 lorsque X = 0. Donc l'équation de la tangente en 0,0 est Y = X. En étudiant la convexité de la fonction log(1 + X), qui est strictement concave, on peut conclure que la courbe est en-dessous de cette tangente, ce qui démontre l'inégalité recherchée. Enfin, on cherche à encadrer sin(X) entre pi/2 et 0 pour X dans l'intervalle [0, pi/2]. On montre que sin(X) est concave dans cet intervalle en calculant sa dérivée seconde qui est -sin(X), et qui est donc négative dans cet intervalle. On démontre ensuite que sin(X) est inférieur ou égal à X en montrant que X est l'équation de la tangente à la courbe de sin(X) en 0. Finalement, on montre que sin(X) est supérieur ou égal à pi/2 en trouvant une corde entre les points (0,0) et (pi/2,1), qui est une droite décroissante. Le maximum de cette droite est atteint en X = 0, et vaut pi/2, ce qui démontre l'encadrement recherché.

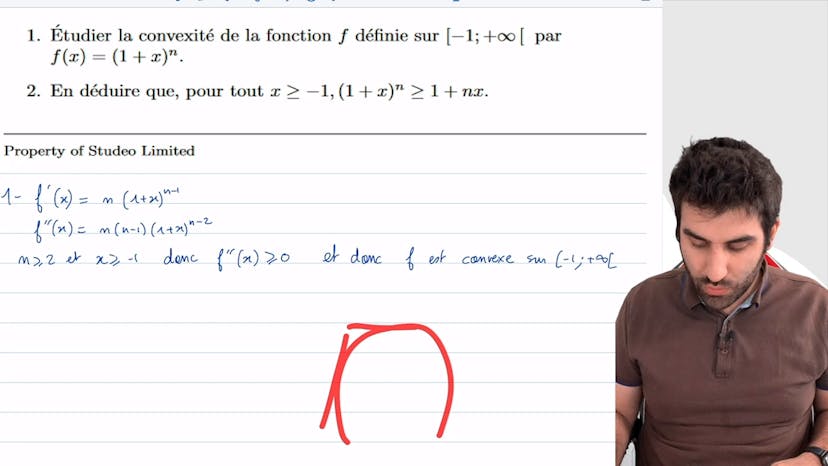
Inégalité de Bernoulli

Dans cet exercice, on montre l'inégalité de Bernoulli en utilisant la convexité de la fonction 1 + x^n. On commence par étudier la convexité de cette fonction en dérivant deux fois et en analysant le signe des dérivées. On conclut que la fonction est convexe sur l'intervalle [-1, +∞]. Ensuite, on utilise cette convexité pour déduire que pour x > -1, la fonction 1 + x^n est plus grande que 1 + nx. On fait cela en considérant l'équation de la tangente à la courbe de la fonction au point d'abscisse 0, qui est donnée par l'équation y = nx + 1. Comme la fonction est convexe, elle est au-dessus de cette tangente, ce qui implique que 1 + x^n est plus grand que 1 + nx. Ainsi, on obtient finalement que 1 + x^n ≥ 1 + nx pour x > -1.

Moyennes arithmétique et géométrique

Dans cet exercice, on étudie l'inégalité entre la moyenne arithmétique, géométrique et harmonique de deux réels positifs x et y. On veut montrer que m < g < h où m est la moyenne arithmétique, g est la moyenne géométrique et h est la moyenne harmonique. On commence par montrer que m < y car x < y. Ensuite, on montre que g < m en utilisant une identité remarquable. On écrit m - g = x + y / 2 - sqrt(xy) = (sqrt(x) - sqrt(y))^2 / 2. Comme (sqrt(x) - sqrt(y))^2 est positif, on conclut que m - g > 0 et donc m > g. Ensuite, on montre que x < g en utilisant le fait que la racine est croissante. Comme x < y, on a sqrt(x) < sqrt(y), ce qui implique x < sqrt(x)*sqrt(y) = sqrt(xy) = g. Finalement, on veut montrer que h est entre x et g. On utilise les inverses des moyennes et on montre que 1/g < 1/h < 1/x. Donc en prenant les inverses, on a g < h < x. Ainsi, on a montré que x < h < g < m < y. On généralise ensuite cette inégalité pour n > 2 en utilisant la concavité de la fonction logarithme. On écrit la moyenne arithmétique comme une somme et la moyenne géométrique comme un produit. On utilise ensuite l'inégalité de concavité du logarithme pour montrer que la somme des logarithmes des xi/n est plus petit qe le logarithme du produit des xi élevés à la puissance 1/n. En utilisant l'équivalence entre le logarithme et l'ordre croissant, on conclut que la moyenne arithmétique est plus petite que la moyenne géométrique.

Points d’inflexion

Dans cet exercice, nous étudions une fonction pour déterminer ses points d'inflexion. Un point d'inflexion est un point où la dérivée seconde d'une fonction change de signe. Pour cela, nous calculons d'abord la dérivée seconde de la fonction. En factorisant cette dérivée seconde, nous pouvons étudier le signe des différents facteurs pour déterminer les points d'inflexion. La dérivée seconde de la fonction est moins cos(3x) fois cos(x) moins cos(2x). Pour étudier le signe de cette expression, nous utilisons quelques formules trigonométriques pour factoriser. Nous factorisons la dérivée seconde par moins cos(2x), ce qui nous donne moins cos(2x) fois (2cos(2x) plus 1). En étudiant le signe de moins cos(2x), nous voyons que cos(2x) est négatif lorsque 2x est entre pi/2 et 3pi/2. Cela signifie que x est entre pi/4 et 3pi/4. En étudiant le signe de 2cos(2x) plus 1, nous trouvons que cela est positif lorsque cos(2x) est supérieur ou égal à -1.5. Cela correspond à x étant entre 0 et 2pi/3, ou entre 7pi/3 et 2pi. En regroupant toutes ces informations, nous pouvons construire un tableau de signes pour la dérivée seconde. Finalement, les seuls changements de signe de la dérivée seconde se produisent lorsque x est égal à pi/4 + (pi/2)k ou à 2pi/3 + (2pi)k, où k est un entier relatif (z). Ainsi, l'ensemble des points d'inflexion de la fonction est donné par les abscisses pi/4 + (pi/2)k et les ordonnées f(pi/4 + (pi/2)k), pour k appartenant à z, ainsi que les abscisses 2pi/3 + (2pi)k et les ordonnées f(2pi/3 + (2pi)k), pour k appartenant à z.

Majoration de f ’ grâce à f ”

Aucun résumé n'est disponible pour cette vidéo

Inégalité de Hölder et Minkowski

Aucun résumé n'est disponible pour cette vidéo

Fonctions convexes avec asymptote

Dans cet exercice, on utilise l'inégalité des pentes pour montrer certains résultats. D'abord, on montre que si la limite de f, lorsque x tend vers l'infini, est 0, alors f est positive sur tout son domaine. On suppose par l'absurde qu'il existe un x0 tel que f(x0) soit strictement négatif. Alors, en utilisant la définition de la limite, on montre qu'il existe un x1 plus grand que x0 tel que f(x1) soit entre f(x0) et 0. En utilisant l'inégalité des pentes, on montre que f(x) est strictement supérieur à cette expression. Cependant, cette expression est une fonction affine dont la limite est l'infini. Donc, on obtient une contradiction avec la limite de f qui est 0. Donc, f ne peut pas être négative, ce qui signifie que f est positive pour tout x. Ensuite, on montre que la somme d'une fonction convexe et d'une fonction affine est convexe. On pose g(x) comme la somme de f(x), une fonction convexe, et ax + b, une fonction affine. On veut montrer l'inégalité de convexité, c'est-à-dire que g(tx + (1-t)y) est plus petite que t*g(x) + (1-t)*g(y) pour tout t entre 0 et 1. En remplaçant g par son expression, on montre que g(tx + (1-t)y) est plus petite que t*g(x) + (1-t)*g(y) en utilisant l'inégalité de convexité de f et en regroupant les termes. Enfin, on suppose que la courbe représentative de f a une asymptote et on veut montrer que la courbe est toujours au-dessus de cette asymptote. On pose y = x + b comme l'équation de l'asymptote de f. On montre que la différence g(x) = f(x) - ax + b tend vers 0 lorsque x tend vers l'infini, car f a une asymptote en plus l'infini. Par la question précédente, on sait que g est convexe et positive, donc on conclut que f(x) est toujours plus grande que ax + b, ce qui signifie que la courbe de f est au-dessus de son asymptote. En résumé, on utilise l'inégalité des pentes pour montrer que si la limite de f est 0, alors f est positive sur tout son domaine. On montre aussi que la somme d'une fonction convexe et d'une fonction affine est convexe, et que si la courbe de f a une asymptote, alors elle est toujours au-dessus de cette asymptote.

Déf fondamentale

Le cours traite du logarithme et de ses propriétés. La fonction logarithme, notée ln, est définie sur l'ensemble des réels strictement positifs. Elle associe à chaque nombre réel positif x, l'unique solution de l'équation exponentielle E^(2y) = x. On utilise le symbole "log" pour indiquer la solution à l'équation E^(2y) = x, ce qui revient à écrire log(x) = y. L'exponentielle de log(x) est toujours égale à x, et réciproquement, le logarithme de l'exponentielle de x est égal à x. Il existe quelques valeurs particulières, tels que log(1) = 0, log(e) = 1 et log(1/e) = -1. Il faut faire attention à ne pas confondre la racine carrée de x², qui donne la valeur absolue de x, avec le logarithme de x, qui est défini uniquement pour les x positifs. La prochaine vidéo abordera d'autres notions liées au logarithme.