Cours d'apprentissage en ligne

Changement de variables 2

Dans cette transcription d'une vidéo sur les changements de variables en calcul d'intégrales, nous abordons trois exemples. Le premier exemple concerne l'intégrale de 0 à 1 de 1/(1+exp(t)) dt. On pose x = exp(t) et on utilise la formule de changement de variable pour obtenir l'intégrale de 1 à e de 1/(x+x^2) dx. On calcule cette intégrale en décomposant la fraction en éléments simples et en utilisant des propriétés des logarithmes. Finalement, on trouve que l'intégrale demandée est égale à 1 + ln(2) - ln(e+1). Le deuxième exemple concerne l'intégrale de 1 à 3 de sqrt(t)(t+1) dt. On pose x = sqrt(t) et on obtient l'intégrale de 1 à sqrt(3) de x^2/(1+x^2) dx. On remarque que le numérateur et le dénominateur se ressemblent beaucoup, on utilise donc la technique du "1 plus 1 moins 1" pour obtenir une intégrale en arctan. Finalement, on trouve que l'intégrale demandée est égale à sqrt(3) - 1 - pi/12. Le troisième exemple concerne l'intégrale de -1 à 1 de sqrt(1-t^2) dt. On pose t = sin(θ) et on obtient l'intégrale de -pi/2 à pi/2 de sqrt(1-sin^2(θ)) cos(θ) dθ. On utilise ensuite des formules trigonométriques pour simplifier l'intégrale. Finalement, on trouve que l'intégrale demandée est égale à pi/2. Il est important de retenir la méthode pour traiter les fractions polynomiales et de s'adapter aux différentes situations de changement de variable. La dynamique est similaire à celle des intégrations par parties, il faut suivre les étapes dans l'ordre et tester différentes approches si nécessaire. Merci d'avoir suivi cette vidéo et à bientôt !

Décomposition en éléments simples

Dans cette vidéo, Matisse de Studio explique comment trouver les primitives de fractions polynomiales spécifiques. Il utilise une méthode précise en fonction du discriminant du dénominateur. Si le discriminant est supérieur ou égal à zéro, il décompose la fraction en éléments simples. Si le discriminant est strictement négatif, il met le dénominateur sous forme canonique. Il commence par résoudre l'exemple de la fonction x/(x²+4). Le discriminant est -16, donc il met le dénominateur sous forme canonique x²+4 = (x+0)²+4. La primitive de 1/(x² + a²) est 1/a * arctan(x/a), donc la primitive de x/(x²+4) est 1/2 * arctan(x/2). Ensuite, il résout l'exemple de la fonction 1/(x²+4x+5). Le discriminant est -4, donc il met le dénominateur sous forme canonique x²+4x+5 = (x+2)²+1. Il utilise le théorème fondamental de l'analyse pour intégrer la forme canonique et obtient que la primitive de 1/(x²+4x+5) est arctan(x+2). Enfin, il résoud l'exemple de la fonction 1/(1-x²). Le discriminant est 4, donc il décompose la fraction en éléments simples et obtient que la primitive de 1/(1-x²) est 1/2 * ln(|1+x|/(1-x)). Il explique également comment résoudre les fractions polynomiales plus générales en simplifiant et en utilisant les propriétés de linéarité de l'intégrale. Il rappelle que selon le cas, les primitives peuvent être en racines carrées ou en arctangente. En conclusion, il récapitule les deux méthodes principales pour trouver les primitives de fractions polynomiales : la décomposition en éléments simples lorsque le discriminant est positif et la mise en forme canonique lorsque le discriminant est négatif. Note: La traduction a été légèrement modifiée pour optimiser le texte en termes de SEO.

Primitives et récurrence

Dans cette vidéo, Mathis de studio présente le calcul d'une infinité d'intégrales. Il pose l'intégrale In égale à l'intégrale de 0 à 1 de dx sur x² plus 1, le tout à la puissance n. La première question consiste à exprimer In+1 en fonction de Im pour tout n. Il commence par rechercher une relation entre le rang d'après et le rang d'avant. En utilisant la technique d'intégration par parties, il obtient deux équations qui le conduisent à une expression entre In+1 et In+2. En utilisant la technique du plus-un-moins-un, Mathis parvient à un résultat final : In+1 = 1 sur 2n+1 fois (n+1) moins 1 sur 2n fois In. Il calcule ensuite In pour n = 1 et trouve que I1 est égal à pi sur 4. En utilisant la formule trouvée précédemment, il calcule également les valeurs de I2 et I3, qui sont respectivement égales à 1 quart plus pi sur 8 et 1 quart plus 3 pi sur 32. Il souligne que cette méthode permet de calculer une infinité d'intégrales pour toute valeur de n. Il encourage les spectateurs à retenir la méthode d'intégration par parties, à ne pas se décourager si une tentative ne fonctionne pas et à utiliser la technique du plus-un-moins-un pour comparer le numérateur et le dénominateur. En conclusion, Mathis remercie les spectateurs et leur dit à bientôt.

Les complexes à l'aide !

Dans cette vidéo, nous étudions le calcul de l'intégrale de 0 à pi de x² exponentiel x cosinus x dx. Pour résoudre ce problème, nous utilisons une astuce en se rappelant que le cosinus peut être représenté comme la partie réelle d'une exponentielle complexe. En utilisant cette propriété, nous réduisons le problème à calculer l'intégrale de 0 à pi de x² exponentiel de 1 plus ix dx. Pour résoudre cette intégrale, nous utilisons une technique d'intégration par parties. En effectuant deux intégrations par parties, nous obtiendrons une expression finale pour l'intégrale initiale. Après avoir calculé cette expression, nous prenons la partie réelle pour obtenir la solution finale de l'intégrale initiale. En résumé, grâce à cette astuce de représenter le cosinus comme une exponentielle complexe, nous avons réussi à calculer l'intégrale initiale. Cette méthode est pratique et permet souvent une résolution réussie.

Intgérales de Wallis

Dans cette vidéo, Matisse de Studio explique comment calculer les intégrales de Wallis. Il commence par définir les intégrales de Wallis en utilisant la fonction sinus et la puissance n. Il pose les équations pour W0 et W1, les deux premières intégrales à calculer. Ensuite, il détermine une relation entre Wn et Wn plus 2 en utilisant la technique d'intégration par parties. Il utilise cette relation pour calculer W2n et W2n plus 1 en fonction de n. Il souligne que ces calculs sont assez complexes et nécessitent une certaine méthode et attention aux détails. Il conclut en donnant les expressions finales pour W2n et W2n plus 1 en utilisant les factorielles et les puissances de 2. Il recommande de refaire cet exercice pour s'entraîner et insiste sur l'importance de comprendre et maîtriser cette méthode pour résoudre ce type de problèmes.

Récurrence costaude

Dans cette vidéo, on parle de calculs de sommes à l'aide d'intégrales. On commence par poser une intégrale IN, qui va de 0 à pi/4, de la tangente du x à la puissance n, dx. On nous demande tout d'abord de calculer I0 et I1, puis de trouver une relation entre IN et IN+2, et enfin d'en déduire IN en fonction de n. Pour calculer I0, on sait que tangente à la puissance 0 est égal à 1. Donc entre 0 et pi/4, I0 vaut pi/4. Pour calculer I1, on utilise la primitive de la tangente qui est le ln du cosinus. Donc entre 0 et pi/4, on obtient 1.5ln(2). Ensuite, on cherche une relation entre Im et Im+2. On utilise une astuce en faisant la somme de tangente de n+2 moins tangente de n+2. Cela nous permet de faire un changement de variable en posant phi égal à tangente de x. On obtient donc une nouvelle intégrale qui est plus simple à calculer, et cela donne Im = 1/(n+1). Ensuite, on détermine les expressions de In en fonction de la parité de l'indice. Si l'indice est pair, In = 1 - (-1)^n. Si l'indice est impair, In = (-1)^(n+1) * ln(2)/2. Ensuite, on montre que In tend vers 0 quand n tend vers l'infini, ce qui permet de déterminer les limites des suites suivantes. La suite Vn est égale à la somme pour k allant de 1 à n de (-1)^(k-1)/k, et elle tend vers pi/2. La suite Un est égale à la somme pour k allant de 1 à n de (-1)^(k-1)/k, et elle tend vers ln(2). En conclusion, on a utilisé des intégrales pour calculer des sommes, et cela nous a permis de trouver des relations entre les différentes sommes et de déterminer leurs limites.

Introduction ED

Une équation différentielle est une équation dont l'inconnue est une fonction. On utilise généralement la variable "x" pour les équations avec des réels, mais pour les équations différentielles, on utilise la variable "y" pour les fonctions. Une primitive "f" est une fonction qui, lorsqu'elle est dérivée, donne la petite fonction "y". Les solutions de l'équation différentielle sont les fonctions qui satisfont cette condition. On peut rencontrer des équations différentielles en physique, par exemple lorsqu'on étudie la trajectoire d'un boulet ou le refroidissement d'une boisson chaude. Ces équations permettent de comprendre comment la vitesse ou la température évolue en fonction de la position ou de la valeur. On peut résoudre les équations différentielles en utilisant des méthodes telles que la méthode des solutions homogènes, la méthode des solutions linéaires simples, ou la méthode des solutions avec une fonction quelconque. C'est pourquoi il est important de connaître ces différentes méthodes.

ED : définitions de base

Ce cours aborde les équations différentielles homogènes, qui sont de la forme y'=ay, avec a non nul. Les solutions de ces équations sont de la forme k*exp(x), avec k une constante. Il y a une infinité de solutions pour cette équation. Cependant, en fixant une condition initiale, il n'y a qu'une seule fonction solution. La démonstration de ce résultat est présentée, en utilisant notamment une approche intuitive. Cette démonstration permet de trouver la forme générale des solutions, qui sont des exponentielles à x. La démonstration est ensuite développée de manière rigoureuse, en montrant que les solutions sont bien de la forme k*exp(x) et en vérifiant que cette forme satisfait bien l'équation différentielle.

Solutions Particulières

Les équations différentielles non homogènes se présentent sous la forme Y' = AY + F, où F est une fonction donnée. La solution à cette équation est la somme de deux termes : une solution homogène (Y' = AY) et une solution particulière (U' = AU + F). La solution homogène est déjà connue grâce au théorème précédent, et peut être écrite sous la forme k exp(AX), où k est une constante. La solution particulière, U, doit être trouvée en s'inspirant de la fonction F. Dans la plupart des cas, U sera de la même famille que F (par exemple, si F est une fonction affine, U sera de la forme AX + B). Dans les exercices plus complexes, on vous donnera des indications sur la famille à utiliser. Il est important de noter que la solution particulière n'est pas unique, mais l'ensemble des solutions sera de la forme U + V, où U est une solution particulière et V est une solution homogène. Il est également intéressant de noter que le cas des équations homogènes est inclus dans ce cas-ci, lorsque la fonction F est nulle. Dans ce cas, U sera égal à zéro. Trouver la solution particulière peut sembler complexe, mais en s'inspirant de la fonction F, on peut généralement trouver une solution de la même famille. Par exemple, si F est une fonction constante, la solution particulière sera également constante. Si F est une fonction quadratique, la solution particulière sera de la forme AX^2 + BX + C, où A, B et C sont des constantes à déterminer. Dans le cas où F est une constante, la solution particulière est simplement moins B sur 1. Il est important de maîtriser ce cas dans le programme. En conclusion, pour résoudre une équation différentielle non homogène, il faut trouver une solution homogène et une solution particulière, en s'inspirant de la fonction F. Avec ces deux termes, on obtient la solution générale de l'équation. En comprenant cette méthode, on peut résoudre la plupart des exercices de ce type. N'hésitez pas à poser des questions et à consulter l'FAQ pour plus de précisions.

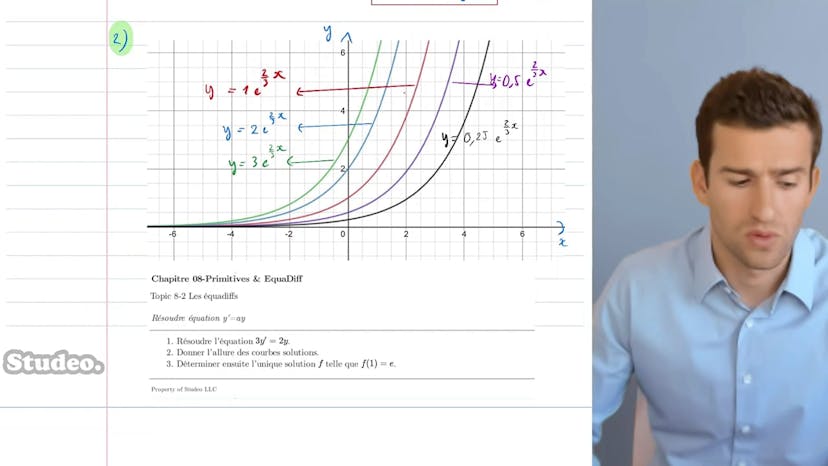
Équation y'=ay

Dans cette vidéo, nous allons apprendre à résoudre une équation différentielle de premier ordre à coefficient constant. Plus précisément, nous allons nous concentrer sur les équations du type y' = y, sans termes de second ordre, et avec des coefficients constants. Nous commençons par étudier l'équation différentielle donnée : 3y' = 2y. Nous divisons les deux côtés par 3 pour obtenir une forme du type y' = 2/3y. Ainsi, nous avons une équation de la forme y' = y, avec a égal à 2/3. En utilisant nos connaissances précédentes sur les équations de ce type, nous savons que les solutions sont de la forme k * e^(ax), où k est une constante réelle et e est la base du logarithme naturel. Dans notre cas, les solutions sont donc k * e^(2/3x), avec k appartenant à R réel. Ensuite, on nous demande de tracer les courbes représentant ces solutions. Ce qui varie ici, c'est la valeur de k, notre constante multiplicatrice. J'ai réalisé quelques exemples en prenant différentes valeurs pour k, allant de 0,25 à 3. Nous observons que plus k augmente, plus la courbe associée "décolle" et s'éloigne de l'axe des x. Il s'agit d'une exponentielle avec une constante multiplicatrice. Toutes ces courbes ont une allure similaire, appartenant à la même famille. Ensuite, on nous demande de déterminer parmi ces courbes celle qui vérifie f(1) = e. Dans les équations différentielles, lorsque nous avons une condition particulière, il existe une unique solution qui satisfait à la fois l'équation différentielle et cette condition particulière. Ici, nous voulons trouver la constante multiplicatrice k en utilisant la condition f(1) = e. Nous supposons que f(x) est de la forme de notre solution, c'est-à-dire k * e^(2/3x). Pour vérifier la condition en x = 1, nous remplaçons x par 1 et obtenons k * e^(2/3). Nous avons alors une simple équation en k que nous résolvons, ce qui donne k = e * e^(-2/3), soit e^(1/3). Ainsi, notre solution finale est f(x) = e^(1/3) * e^(2/3x). Ceci est une méthode très courante et classique pour résoudre une équation différentielle du type y' = y avec une condition initiale. Si vous avez des questions supplémentaires, veuillez consulter la FAQ.

Équation y'=ay+b

Aujourd'hui, nous allons nous intéresser à la résolution des équations différentielles du premier ordre avec un second membre, c'est-à-dire les équations de la forme y' = y + b. La méthode est assez simple : nous commençons par chercher une solution constante, que nous appelons la solution particulière. Ensuite, nous résolvons l'équation homogène, qui est y' = y. Enfin, nous combinons ces deux solutions pour obtenir la solution générale. Prenons l'exemple de l'équation y' = -y + 3, où a = -1 et b = 3. Nous résolvons d'abord l'équation homogène y' = -y, dont les solutions sont de la forme y(x) = ae^(-x), où a est une constante réelle. Ensuite, nous recherchons une solution particulière constante, en supposant que sa dérivée est nulle. En injectant cette solution dans l'équation, nous trouvons que phi = 3. Enfin, nous combinons ces deux solutions pour obtenir la forme générale de la solution y(x) = e^(-x) + 3a, où a est une constante multiplicative inconnue. Il est important de noter qu'il y a toujours une constante multiplicative dans la solution générale. Parfois, pour déterminer sa valeur, nous avons besoin d'une condition particulière, par exemple y(alpha) = beta. Dans ce cas, il y aura une unique solution qui vérifiera cette condition particulière. Voilà comment résoudre une équation différentielle du premier ordre de la forme y' = y + b. N'hésitez pas à poser vos questions dans la description.