 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc

Application à la physique
Dans cette vidéo, nous résolvons des équations différentielles de physique. Nous commençons par l'équation classique du premier ordre, qui peut être utilisée pour décrire une activité radioactive, un freinage avec frottement fluide ou un circuit RL ou RC. Sa solution générale est x(t) = x0 - x∞ * exp(-t/τ), avec x0 étant la position initiale et x∞ étant la position à l'infini. Ensuite, nous étudions l'équation de décharge d'un condensateur, où la solution générale est u(t) = u0 - e * exp(-t/RC), avec u0 étant la tension initiale. Ensuite, nous abordons l'équation de l'oscillateur harmonique, où la solution générale est x(t) = A * cos(ω0 * t) + B * sin(ω0 * t), avec A et B étant déterminés par les conditions initiales. Enfin, nous résolvons l'équation de charge dans les circuits RLC, où la solution générale dépend du signe du discriminant et des conditions initiales. La méthode utilisée est de trouver d'abord la solution homogène en résolvant l'équation caractéristique, puis de trouver une solution particulière en posant une constante appropriée. En appliquant les conditions initiales, nous déterminons les valeurs des constantes et obtenons l'unique solution de l'équation différentielle. Finalement, nous concluons que la résolution technique des équations différentielles en physique ne présente pas de grandes difficultés, tant que l'on applique correctement la méthode et que l'on connaît les formules nécessaires.
Maths SM&SP
Analyse
2BAC SM Maroc

Changement variable classique
Dans cette vidéo, Matisse de Studio résout une équation différentielle d'ordre 2 en utilisant un changement d'inconnu. L'équation à résoudre est AX2Y2 + BX' + CY = 0, avec A, B et C étant des réels et A étant différent de 0 pour X entre 0 et l'infini. Cela pose un problème car notre méthode habituelle ne fonctionne pas avec cette équation.
Cependant, nous sommes guidés vers une solution. On nous demande de vérifier que si Y est deux fois dérivable sur 0 et plus infini, alors Z est deux fois dérivable sur R, et vice versa. On prouve cela en utilisant la composition et les théorèmes généraux.
Ensuite, nous effectuons le changement d'inconnu en remplaçant Y par Z ln X dans l'équation différentielle. Après simplification, nous obtenons une équation linéaire du second ordre à coefficients constants. C'est une équation que nous sommes capables de résoudre.
Nous résolvons l'équation homogène et trouvons une solution générale. En composant cette solution avec ln X, nous trouvons l'ensemble des solutions de l'équation différentielle initiale.
En résumé, grâce à un changement d'inconnu, nous avons transformé l'équation différentielle en une équation linéaire du second ordre à coefficients constants, que nous savons résoudre. Nous avons utilisé des techniques de composition pour trouver l'ensemble des solutions de l'équation initiale.
Maths SM&SP
Analyse
2BAC SM Maroc
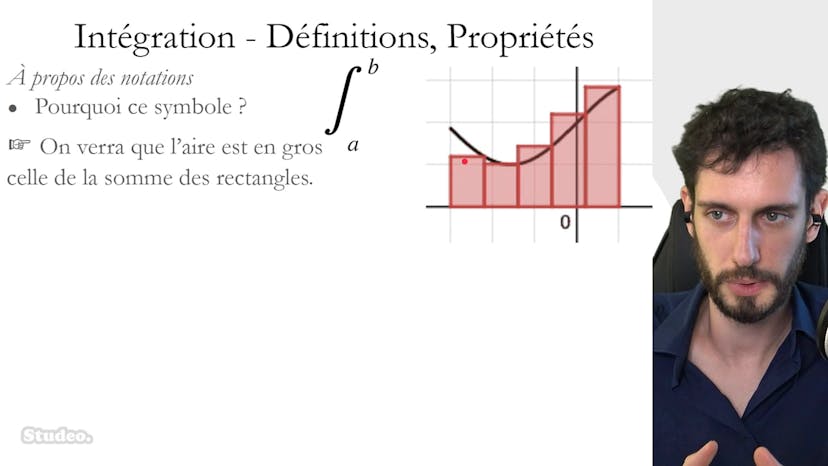
Introduction
Bienvenue dans cette vidéo d'introduction au premier sujet du chapitre sur les intégrales. Dans cette vidéo, nous allons présenter les définitions et les propriétés des intégrales. L'objectif de ce chapitre est de calculer des "R" sous des courbes, c'est-à-dire d'évaluer l'aire entre une courbe et l'axe des x. Dans ce sous-chapitre, nous allons poser les bases pour les fonctions continues et examiner ce qui se passe lorsqu'elles sont positives ou négatives. Pour commencer, prenons un exemple simple ensemble. Quelle est l'aire "R" sous la courbe de cette fonction ? La fonction est constante et vaut 2 entre 0 et 3. Il s'agit d'un rectangle de hauteur 2 et de largeur 3, donc l'aire "R" est de 6. Nous pouvons faire la même chose avec une fonction affine qui a une pente de 1. Cette fois-ci, nous avons un triangle rectangle isocèle avec une base de 3 et une hauteur de 3. L'aire "R" est donc égale à 3 fois 3 divisé par 2, soit 9/2. Maintenant, vous pourriez vous demander pourquoi consacrer un chapitre entier à ce sujet. En réalité, nous aurons affaire à des fonctions plus complexes et nous allons nous inspirer de cas très simples, comme les rectangles, pour essayer de comprendre comment évaluer l'aire "R" sous des fonctions plus courbes qui ne sont pas constantes. Nous dirons donc que cela sera approximativement égal à l'aire "R" d'une somme de rectangles. Les rectangles auront une largeur "delta x" pour la distance entre les points, et une hauteur qui sera la valeur de la fonction "f(x)" pour chaque rectangle. Pour être plus précis, il s'agit d'une approximation, mais je vais devoir vous expliquer pourquoi nous utilisons ce symbole. Ce symbole est en réalité un S stylisé qui signifie somme entre "a" et "b". Mais qu'est-ce qui se passe ? En réalité, nous verrons que l'aire "R" est grossièrement égale à la somme des rectangles, mais uniquement lorsque nous effectuons une somme sur un nombre infini de rectangles. Nous allons donc placer un nombre infini de rectangles en les rendant infiniment fins pour approcher la vraie valeur. En termes d'écriture, nos rectangles, qui ont une largeur "delta x", sont souvent représentés avec un "dx" lorsque le nombre de rectangles devient très grand. Nous utilisons également un symbole de somme stylisé lorsque la somme devient infinie, c'est-à-dire lorsque nous atteignons une "R" complète. Maintenant que nous avons expliqué comment cela fonctionne et pourquoi nous utilisons ces symboles, nous allons aborder les premières approximations que nous allons faire. Les points clés de ce sous-chapitre seront les définitions des intégrales pour les fonctions continues positives et pour les fonctions de signes quelconques. Nous utiliserons également des encadrements et des intuitions graphiques pour estimer l'aire "R". Les méthodes que nous utiliserons seront le calcul de l'aire "R" et l'estimation de l'aire "R" par la méthode des rectangles que nous avons évoquée précédemment. Bon courage pour le reste du chapitre et je vous retrouve dans la prochaine vidéo. N'hésitez pas à poser des questions dans la FAQ si besoin. À bientôt !
Maths SM&SP
Analyse
2BAC SM Maroc

Définition de l'intégrale
L'intégrale d'une fonction continue et positive sur un intervalle [a, b] représente l'aire sous la courbe de cette fonction entre les valeurs x = a et x = b, ainsi que l'axe horizontal. On exprime cette aire en unités d'aire, qui sont des carrés de taille 1 sur 1 dans un repère orthonormé. L'intégrale est notée par le symbole mystérieux entre a et b de f(x) dx. Si la fonction est négative, on considère l'aire comme négative et on met un signe moins devant la valeur de l'aire calculée. Si la fonction présente des parties positives et des parties négatives, on comptabilise les aires séparément. Il est important de noter que l'intégrale est positive lorsque la fonction est au-dessus de l'axe horizontal et négative lorsqu'elle est en dessous.
Maths SM&SP
Analyse
2BAC SM Maroc

Encadrement et intuition graphique
Dans cette vidéo, différentes méthodes d'approximation de l'aire sous une courbe sont présentées. L'objectif est de mieux comprendre le calcul de l'aire.
La méthode principale est celle des rectangles supérieurs et inférieurs. On divise l'intervalle en plusieurs petits intervalles de même amplitude et on construit des rectangles en dessous et au-dessus de la courbe. En augmentant le nombre de rectangles et en diminuant leur taille, on s'approche de plus en plus de la vraie aire sous la courbe.
D'autres méthodes sont également mentionnées, bien qu'elles ne soient pas au programme. Il s'agit de la méthode du point milieu, où des rectangles sont traversés par la courbe au milieu de leur côté supérieur, et de la méthode des trapèzes, où les quadrilatères ne sont plus des rectangles mais des trapèzes.
Ces méthodes permettent d'obtenir des approximations plus précises de l'aire sous la courbe. La vidéo illustre ces différentes méthodes à l'aide de graphiques pour faciliter la compréhension.
En conclusion, cette vidéo offre un aperçu des différentes façons d'approximer l'aire sous une courbe, mettant en évidence leur utilité et leur précision croissante avec l'augmentation du nombre de rectangles utilisés.
Maths SM&SP
Analyse
2BAC SM Maroc
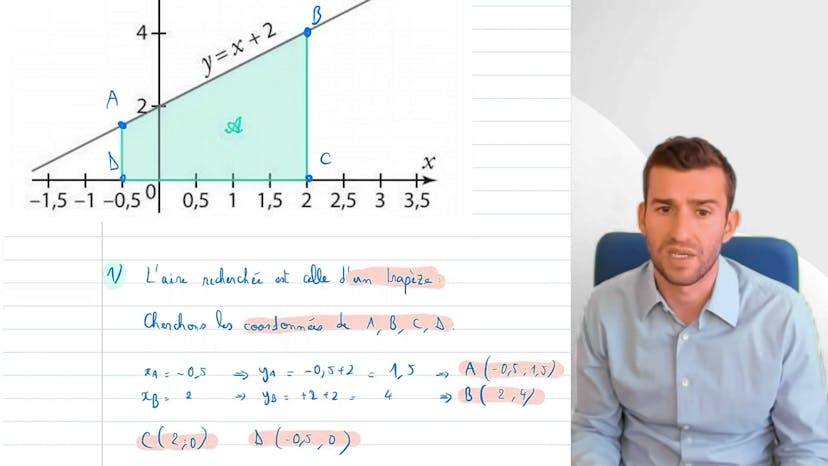
Intégrale et Aire
Lorsque nous souhaitons calculer une intégrale de façon géométrique, sans utiliser une fonction, il est important que la forme géométrique soit « simple ». Dans cet exemple, nous avons une fonction affine pour laquelle l'erreur d'intégration correspond à un trapèze. Nous nous intéressons ici à l'intégrale de la fonction x plus 2 entre -0,5 et 2. Nous pouvons représenter cette intégrale comme l'erreur sous la courbe jusqu'à l'axe des abscisses.
Il existe deux méthodes pour calculer cette intégrale. La première consiste à calculer la primitive de x plus 2 et à effectuer les calculs habituels. La seconde méthode consiste à réaliser un calcul géométrique de l'erreur, étant donné que celle-ci correspond à un trapèze. Dans cette dernière méthode, nous devons déterminer la hauteur, la largeur et la longueur des bases du trapèze.
Pour trouver ces informations, nous avons choisi de trouver les coordonnées des points a, b, c et d. Les points a et b se trouvent sur la droite de la fonction et vérifient donc son équation. Nous connaissons les abscisses : xa est égal à -0,5 et xb est égal à 2. Pour trouver les ordonnées respectives de ces points, nous utilisons l'équation de la droite, à savoir y = x + 2. Ainsi, si xa vaut -0,5, nous avons ya = -0,5 + 2, ce qui donne 1,5. Les coordonnées de a sont donc (-0,5 ; 1,5). De manière similaire, si xb vaut 2, nous avons yb = 2 + 2, soit 4. Les coordonnées de b sont donc (2 ; 4). En ce qui concerne les points c et d, ils se trouvent sur l'axe des abscisses et leurs coordonnées sont respectivement (2 ; 0) et (-0,5 ; 0).
Nous devons maintenant calculer les différentes longueurs des côtés du trapèze. Comme il s'agit de lignes horizontales ou verticales, cela est relativement simple. Pour les côtés a et d, nous faisons la différence entre les ordonnées de a et d, ce qui donne 1,5. Pour les côtés b et c, nous faisons la différence entre les ordonnées de b et c, ce qui donne 4. Pour les côtés d et c, nous faisons la différence entre les abscisses de c et d, ce qui donne 2,5.
En utilisant la formule de l'aire du trapèze, qui est la moyenne des deux bases multipliée par la hauteur, nous pouvons alors calculer l'aire de notre trapèze. Dans notre cas, cela donne (1,5 + 4) * 2,5, ce qui équivaut à 6,875. La formule de l'aire du trapèze dépend de la définition des bases et de la hauteur, mais peu importe la définition choisie, il s'agit de la moyenne des deux côtés parallèles de longueurs différentes, multipliée par la base. Dans notre exemple, nous l'avons vu comme la base multipliée par la moyenne des hauteurs.
Ainsi, nous avons présenté un cas particulier où il n'est pas nécessaire de calculer les primitives de la fonction pour obtenir l'intégrale, mais il est possible d'utiliser le calcul direct de l'aire géométrique, en l'occurrence ici, du trapèze. C'est une méthode alternative pour calculer une intégrale en se basant sur une approche géométrique.
Maths SM&SP
Analyse
2BAC SM Maroc
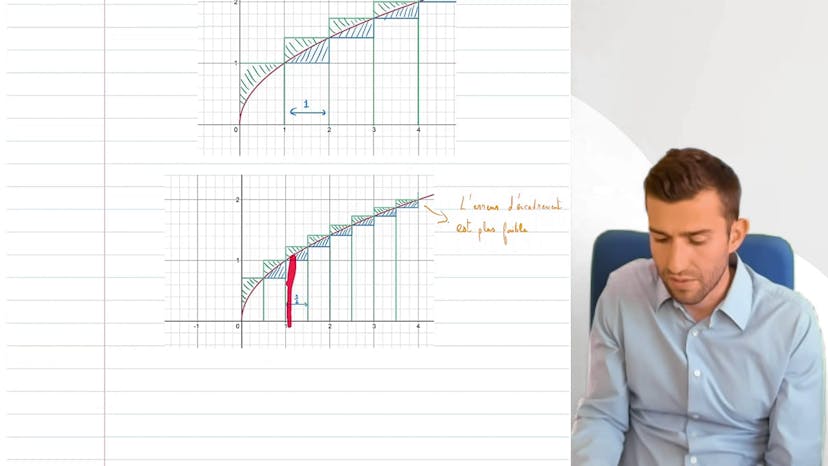
Méthode des Rectangles
L'intégrale de Riemann est une méthode utilisée pour calculer des aires sous des courbes géométriques complexes. Elle consiste à encadrer cette aire en utilisant la méthode des rectangles.
Dans cette vidéo, la courbe intégrée n'a pas une forme géométrique simple, ce qui rend difficile le calcul direct de l'aire. Cependant, en utilisant la méthode des rectangles, il est possible de l'encadrer.
L'idée est de diviser l'aire totale en petits rectangles, en choisissant une largeur appropriée. On peut ainsi obtenir une approximation de l'aire sous la courbe en sommant les aires des petits rectangles.
L'encadrement obtenu sera moins précis si la largeur des rectangles est plus grande, et plus précis si la largeur est plus petite. En augmentant la précision, on se rapproche de l'aire réelle sous la courbe.
Dans l'exemple donné, l'objectif est d'encadrer l'aire sous la courbe de 0 à 4. La courbe est croissante et la fonction f(y) est connue (racine de x). En calculant les aires des petits rectangles, on obtient un encadrement de cette intégrale.
Il est possible d'améliorer la précision de l'encadrement en diminuant la largeur des rectangles. En faisant tendre cette largeur vers zéro, les rectanglres se rapprochent de la courbe géométrique, et l'encadrement devient plus précis.
Il est à noter que cette méthode d'encadrement est utilisée lorsqu'on ne peut pas trouver une primitive de la fonction pour calculer directement l'intégrale.
En conclusion, l'intégrale de Riemann est une méthode permettant de calculer des aires sous des courbes géométriques complexes en utilisant la méthode des rectangles. L'encadrement obtenu dépend de la largeur des rectangles et peut être amélioré en diminuant cette largeur.
Maths SM&SP
Analyse
2BAC SM Maroc

Introduction
Dans ce sous-chapitre sur les intégrales et leur lien avec les primitives, nous allons comprendre comment calculer exactement les R sous une courbe, sans approximation. Jusqu'à présent, nous pouvions seulement trouver des approximations précises en ajoutant un nombre de rectangles, mais cela ne nous donnait pas de résultats exacts pour les fonctions autres que les fonctions affines et constantes. Nous allons découvrir qu'en réalité, il existe un lien exact entre le calcul des R et les primitives. Ce lien fonctionne dans les deux sens : nous pourrons calculer exactement les R en utilisant les primitives, mais nous pourrons aussi, grâce à ce lien, étudier des primitives qui ne sont pas calculables avec les fonctions usuelles. Par exemple, en statistique, nous avons souvent besoin de calculer la primitive de la fonction exponentielle moins x², qui est à l'origine de la courbe en cloche. Malheureusement, il n'existe pas de primitive de cette fonction avec les fonctions usuelles, ce qui nous oblige à faire une approximation numérique en calculant les R. Dans la suite du chapitre, nous verrons également différentes propriétés des intégrales, qui seront intéressantes pour les physiciens et les mathématiciens. En résumé, ce sous-chapitre aborde le lien entre les primitives et les R sous une courbe, avec le théorème fondamental, la condition suffisante d'existence d'une primitive, ainsi que des propriétés générales telles que la relation de Schall, la linéarité, la positivité et la croissance, et des inégalités. Nous aborderons également différentes méthodes pour calculer les intégrales en utilisant les primitives, la linéarité, la relation de Schall, pour encadrer une intégrale, et pour étudier les variations d'une fonction définie par une intégrale. N'hésitez pas à poser vos questions dans la FAQ et je vous retrouve dans la prochaine vidéo !
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème fondamental : énoncé
Dans cette vidéo, le professeur présente le théorème fondamental de l'analyse, qui concerne la notion de primitive et d'intégrale. Il explique que si f est une fonction continue et positive sur un intervalle [a, b], alors la fonction F définie par l'intégrale entre a et x de f sera dérivable et sa dérivée sera égale à f. Cela signifie que F est une primitive de f.
Le professeur illustre ce théorème à l'aide d'un graphique représentant une fonction parabolique négative. Il calcule alors l'aire sous la courbe entre différents points de l'intervalle et trace une fonction qui représente la valeur approximative de cette aire. Il observe que lorsque l'aire est négative, la fonction décroît, et lorsque l'aire est positive, la fonction croît.
Il souligne également que la fonction tracée ressemble à une fonction cubique, ce qui renforce l'idée que cette fonction est une primitive de la fonction initiale.
Le professeur conclut en expliquant qu'il démontrera formellement ce lien entre aire et primitive dans une prochaine vidéo, mais que cette visualisation graphique est essentielle pour comprendre cette notion. Il encourage les spectateurs à poser des questions s'ils ont besoin de précisions.
Maths SM&SP
Analyse
2BAC SM Maroc

Intégrale et Primitive : calcul
Dans cette vidéo, on présente une démonstration d'une propriété fondamentale en mathématiques. On précise qu'il y a une différence entre une propriété et un théorème. Dans ce cas, la propriété indique qu'on peut calculer une intégrale en utilisant une primitive. On utilise le théorème fondamental pour démontrer cela. On donne une fonction f continue et positive sur un intervalle a,b, et on prend une primitive F de f sur cet intervalle. On dit que l'aire entre a et b de la fonction f est égale à F(b) - F(a). On peut aussi écrire cela de manière plus compacte en utilisant la notation [F(x)]_a^b. Ensuite, on généralise cette définition pour les fonctions qui ne sont pas forcément positives en utilisant la même formule. On montre ensuite la démonstration de cette propriété en considérant deux cas : si F est la même fonction que dans le théorème fondamental, ou si F est une autre primitive de f. Dans les deux cas, on montre que l'intégrale de f entre a et b est égale à F(b) - F(a). Cette démonstration montre l'importance des primitives dans le calcul d'intégrales.
Maths SM&SP
Analyse
2BAC SM Maroc

Propriétés 1 : intuitives !
Dans cette vidéo, nous abordons les propriétés intuitives de l'intégrale. La première propriété est la linéarité. Elle dit que si vous prenez l'aire sous une courbe lambda f, cela équivaut à lambda fois l'aire sous la courbe f. De plus, si vous cumulez deux fonctions f et g, l'aire totale sera égale à l'aire de f plus l'aire de g.
En ce qui concerne les bornes, si f est une fonction continue sur un intervalle i avec a et b des réels, l'intégrale de f entre a et a est égale à zéro, car vous prenez l'aire d'un fil qui n'a pas de deuxième dimension. De plus, nous convenons que l'intégrale entre b et a est égale à l'opposé de l'intégrale entre a et b.
Enfin, la relation de Schall indique que si vous additionnez l'intégrale entre a et c et l'intégrale entre c et b, cela équivaut à l'intégrale entre a et b directement. Cela signifie que l'aire totale de la fonction est la même, quelle que soit la valeur de c.
En résumé, ces propriétés intuitives de l'intégrale sont relativement simples. Elles concernent la linéarité, les bornes et la relation de Schall. J'espère que ces explications SEO friendly vous sont claires. À bientôt pour une nouvelle vidéo sur d'autres propriétés de l'intégrale.
Maths SM&SP
Analyse
2BAC SM Maroc
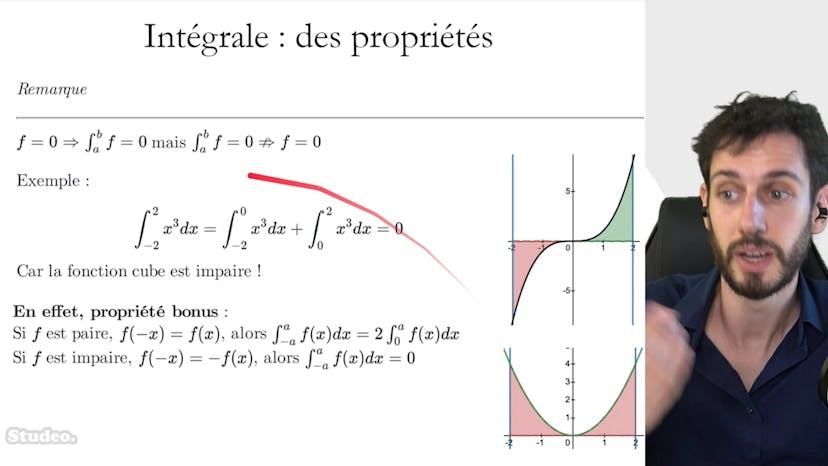
Propriétés 2 : remarques pratiques
Ce cours traite des propriétés des fonctions et de leurs intégrales. La première propriété explique que si une fonction est nulle, son intégrale sera également nulle. Cependant, il est important de noter qu'une fonction dont l'intégrale est nulle sur un intervalle donné n'est pas forcément nulle elle-même. Un contre-exemple est donné pour illustrer ce point.
Ensuite, une propriété bonus est présentée : si une fonction est paire, c'est-à-dire que pour tout x, f(-x) est égal à f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera deux fois l'intégrale sur la moitié de cet intervalle. À l'inverse, si une fonction est impaire, c'est-à-dire que pour tout x, f(-x) est égal à -f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera nulle.
La dernière propriété bonus concerne les fonctions périodiques. Si une fonction a une période T, alors pour tout x, f(x+T) sera égal à f(x). De plus, l'intégrale sur un intervalle de longueur T sera égale à l'intégrale sur un intervalle de taille T centré sur 0.
Ces propriétés sont utiles pour gagner du temps dans l'étude des fonctions et leurs intégrales. Il est donc important de les comprendre et de les utiliser correctement. Le cours se termine en invitant les spectateurs à regarder la prochaine vidéo pour plus d'informations.


