Cours d'apprentissage en ligne

Aire sous une Courbe : Calcul

Dans ce cours, nous abordons le calcul des erreurs sous une courbe à l'aide d'intégrales. Nous allons prendre deux exemples pour calculer ces erreurs, ce qui revient à calculer des intégrales. Le premier exemple concerne l'erreur entre la courbe CF dont l'équation est f2x = x²-4, et l'axe d'étape 6 entre les droites d'équation x = -2 et x = 2. Mathématiquement, cela se traduit par l'intégrale de x²-4dx entre -2 et 2. Nous devons trouver la primitive de la fonction à l'intérieur de l'intégrale. Pour cela, nous posons f2x = x²-4, une fonction polynomiale pour laquelle nous trouvons facilement une primitive. Nous prenons la primitive de chaque terme, soit un tiers de x au cube moins 4x. Ensuite, nous utilisons le théorème fondamental pour trouver l'erreur, qui est égale à un tiers de x au cube moins 4x entre -2 et 2. Après les calculs, nous obtenons -32/3 pour l'erreur. Le deuxième exemple concerne l'erreur entre la courbe et l'axe des abscisses entre les droites d'équation x = -5 et x = 1. Nous devons calculer l'intégrale de x²-4 entre -5 et 1. Encore une fois, la primitive de la fonction reste la même, seules les bornes changent. Après simplification, nous obtenons 18 pour l'erreur. Il est important de noter que la variable d'intégration est x, ce qui signifie qu'elle ne peut pas être utilisée ailleurs dans la fonction. Dans le premier exemple, l'erreur est négative car la partie sous la courbe est située en dessous de l'axe des abscisses. Dans le deuxième exemple, la somme des parties positives et négatives de la courbe nous donne une erreur positive de 18. Pour plus d'informations, vous pouvez consulter la FAQ.

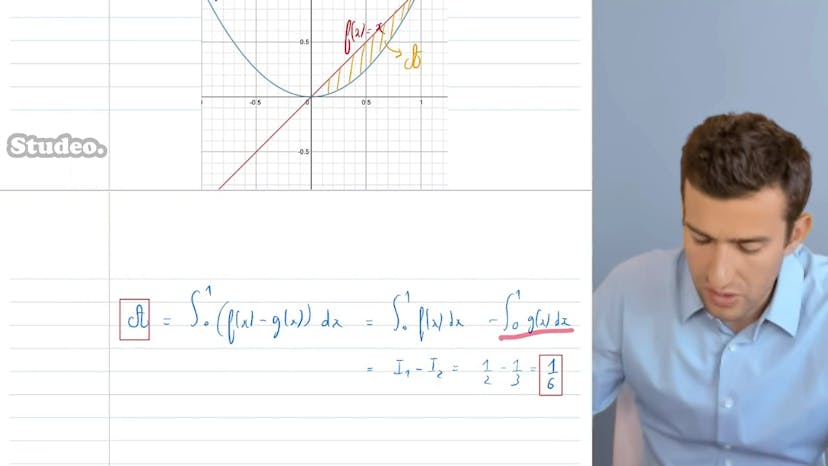
Aire entre 2 Courbes

Dans ce cours, nous allons apprendre à calculer "R" entre deux courbes. Les courbes données sont f(x) = x et g(x) = x², et nous voulons calculer "R" entre elles, dans l'intervalle de x = 0 à x = 1. Pour effectuer ce calcul, nous devons tout d'abord trouver les primitives des deux fonctions f et g. Les primitives de f(x) = x et g(x) = x² sont respectivement F(x) = x²/2 et G(x) = x³/3. Ensuite, nous utilisons le théorème fondamental du calcul intégral. Visuellement, l'R se situe sous la courbe entre f et g. Dans notre cas, nous voulons prendre une valeur positive pour l'R. Donc, nous calculons la différence entre la fonction qui est supérieure à l'autre sur l'intervalle donné. Dans notre cas, f est toujours supérieure à g pour tous les x de 0 à 1. Donc, nous calculons l'intégrale de f(x) - g(x) de 0 à 1 pour obtenir la valeur de notre R. En appliquant les propriétés de l'intégrale, nous obtenons l'intégrale de 0 à 1 de f(x) - l'intégrale de 0 à 1 de g(x). Nous avons déjà calculé ces intégrales et les avons appelées I1 et I2. En utilisant le théorème fondamental du calcul intégral, nous trouvons que I1 = 1/2 et I2 = 1/3. Donc, la différence entre 1/2 et 1/3 est égale à 1/6. Donc, l'R entre les deux courbes, dans l'intervalle de 0 à 1, est égal à 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.

Calcul Valeur Moyenne

Dans ce cours, nous abordons le calcul de la valeur moyenne d'une fonction. Nous avons deux exemples avec des fonctions différentes et des intervalles légèrement différents. La valeur moyenne est l'intégrale de la fonction sur l'intervalle, divisée par la largeur de cet intervalle. Dans notre exemple, la largeur de l'intervalle est de 4 (2 - (-2)). Pour la première fonction f, nous trouvons une primitive h en utilisant le théorème fondamental. En faisant les calculs, nous obtenons 13/3 comme résultat pour l'intégrale de f sur l'intervalle. Pour la deuxième fonction g, nous devons d'abord trouver une primitive de g en utilisant la méthode du quotient. Nous remarquons que nous avons un quotient avec un coefficient manquant, mais nous le faisons apparaître en multipliant par 1/2 * 2. La primitive de g est alors 1/2 ln(|x² - 3|). En appliquant la définition de la valeur moyenne à g, nous trouvons l'intégrale de g sur l'intervalle et effectuons les calculs nécessaires. Nous obtenons une expression avec un ln de (16 - 3), que nous ne pouvons pas simplifier davantage. En résumé, le calcul de la valeur moyenne d'une fonction consiste simplement à appliquer la définition et à effectuer un calcul intégral.

Suite d'Intégrales

La méthode utilisée pour étudier la convergence d'une suite d'intégrales est présentée dans ce cours. La suite de fonctions fn est définie comme 1/(1+t)^n. L'objectif est de trouver la convergence de cette suite. La première méthode consiste à construire des inégalités. En utilisant les propriétés des puissances et des fonctions inverses, on montre que la fonction est encadrée entre 1 et 1-(1+t)^n. Cependant, cette méthode ne fonctionne pas pour la deuxième inégalité. Une autre approche consiste à prendre la différence entre les deux expressions et à montrer qu'elle est positive. En simplifiant l'expression, on obtient une forme du type a^2 - b^2, ce qui permet de conclure que 1-(1+t)^n est inférieur à 1/(1+t)^n. Ensuite, on calcule l'intégrale de 1- t^n de 0 à 1 et on trouve (n/(n+1)). On utilise ensuite la linéarité de l'intégrale pour encadrer cette intégrale. Finalement, on montre que la suite des intégrales converge vers 1 à l'aide du théorème d'encadrement. On utilise les informations précédentes pour conclure que la suite converge et donner sa limite.

Théorème de Rolle

Dans ce cours, nous allons voir comment utiliser le théorème de Rolle de manière efficace. Le théorème de Rolle se présente sous forme d'exercices, notamment avec une petite astuce pas facile à comprendre. Pour commencer, nous considérons une fonction f définie sur un intervalle i, de classe Cn, qui s'annule en n plus un point distinct de i. Nous voulons montrer que la dérivée n s'annule au moins une fois sur i, puis que la dérivée n-1 de f'αf s'annule également au moins une fois sur i. La première méthode consiste à utiliser la récurrence. Nous démontrons la propriété suivante pk : la dérivée km s'annule n plus une moins k fois au moins sur i. Pour l'initialisation, nous n'avons pas de problème. Par hypothèse, fk s'annule n plus une moins k fois. Nous voulons montrer que la dérivée k plus unième s'annule n moins k fois au moins. Nous appliquons le théorème de Rolle sur chaque intervalle ij défini par les points αj et αj plus 1. Ainsi, nous avons n moins k intervalles sur lesquels la dérivée s'annule au moins une fois. En utilisant le théorème de Rolle, nous démontrons que fk plus 1 s'annule au moins n moins k fois. Cette démonstration par récurrence fonctionne parfaitement. Pour la question 2, nous introduisons une fonction h qui est égale à f de x multiplié par e de alpha x. En dérivant h, nous obtenons h prime qui est égal à f prime plus alpha f fois e de alpha f. L'astuce ici est que nous pouvons appliquer le théorème de Rolle sur chaque point où h s'annule, car si h prime s'annule au moins une fois, cela signifie que le terme f prime plus alpha f s'annule également au moins une fois. En utilisant les hypothèses précédentes, nous appliquons le théorème de Rolle et retrouvons que la dérivée enième de f prime plus alpha f s'annule au moins une fois. Ainsi, nous pouvons utiliser le théorème de Rolle dans des exercices en utilisant une petite astuce pour simplifier la démonstration.

Formule de Taylor Lagrange

Le cours traite de la notion de point fixe dans le cadre de suites définies par récurrence et de fonctions définies en escalier. Il explique comment déterminer si un point est récursif ou attractif en se basant sur certaines propriétés de la fonction dérivée. L'astuce utilisée est de poser g(x) = f(x) - x et d'appliquer le théorème des accroissements finis pour prouver l'unicité du point fixe. Ensuite, il démontre que dans une suite définie par récurrence, les termes convergent vers le point fixe en utilisant une démonstration par récurrence. Enfin, il explique que le caractère attractif du point fixe dépend de la pente de la fonction, qui doit être inférieure à 1. Le cours se termine en soulignant l'importance de cette notion dans la résolution d'exercices et d'épreuves.

Règle de l’Hopital

La règle de l'hôpital est un théorème mathématique intéressant qui n'est pas enseigné en France, mais qui est au programme dans certains pays tels que l'Angleterre ou le Luxembourg. Ce théorème permet de calculer la limite d'une fonction indéterminée en utilisant les dérivées des fonctions en question. Pour appliquer cette règle, il faut que les fonctions soient continues et dérivables sur un intervalle donné. Le théorème des accroissements finis généralisé est utilisé pour démontrer la règle de l'hôpital. Il permet de calculer la dérivée d'une fonction composée de deux autres fonctions. Grâce à cette démonstration, on peut ensuite appliquer la règle de l'hôpital à des exemples concrets. La règle de l'hôpital est utile lorsqu'on se retrouve avec une forme indéterminée dans le calcul d'une limite. Elle permet de remplacer une fonction indéterminée par une autre fonction dont la limite est connue. Deux exemples sont donnés pour illustrer l'utilisation de la règle de l'hôpital. Dans le premier exemple, on calcule la limite d'une fonction (x-sin(x))/x^3 en utilisant la règle de l'hôpital. Dans le deuxième exemple, on calcule la limite d'une fonction ln(1+x)-x/x^2 en utilisant également la règle de l'hôpital. Il est précisé que les développements limités sont utilisés pour simplifier les calculs dans ces exemples, mais que leur compréhension complète nécessite des connaissances supplémentaires. En conclusion, la règle de l'hôpital est un outil puissant pour calculer des limites de fonctions indéterminées, mais elle n'est pas enseignée en France. Cependant, il est possible d'avoir à la démontrer dans un exercice, comme cela a été fait dans cet cours.

Polynome de Legendre

Les polynômes de Legendre sont une famille de polynômes qui se montrent sous la forme Pn(x) = (dérivée énième de x²-1 à la puissance n). Ces polynômes ont un degré de 2n et ont un coefficient dominant de (2n factorial / n factorial). En examinant la dérivée de Pn, on peut déterminer les racines du polynôme, notamment les racines d'ordre n-k et les racines d'ordre 1. En appliquant le théorème de Rolle, on peut montrer que Pn a n points distincts d'annulation. Les polynômes de Legendre sont souvent rencontrés dans le domaine des polynômes et il est important de retenir leur forme et leurs propriétés.

Corde et tangente

Dans cet exercice, on cherche à démontrer qu'il existe un certain point où la corde et la tangente d'une fonction sont confondues. Pour cela, nous étudions une fonction f qui vérifie certaines conditions : elle est définie de 0 à 1 dans R, continue et dérivable (de classe c1), et f(0) = f'(0) = f'(1) = 0. On commence par rappeler l'équation de la tangente et de la corde au point c de la courbe. La tangente est représentée par une droite qui passe par le point m de la courbe et a une pente égale à la dérivée de f au point c. La corde est une droite reliant le point m au point o, avec une pente égale à f(c)/c. Pour que la corde et la tangente soient confondues, elles doivent passer par le même point m et avoir la même pente. Ainsi, on cherche un point c où f'(c) = f(c)/c. 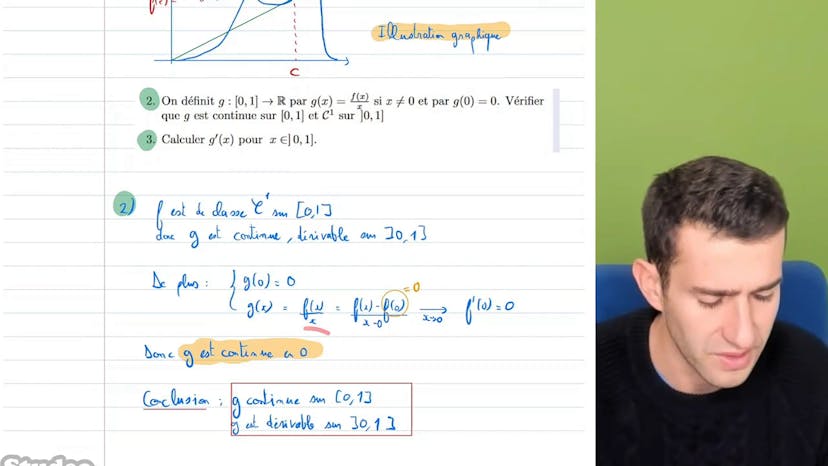On introduit une fonction auxiliaire g(x) = f(x)/x et on montre qu'elle est continue sur [0,1] et de classe c1 sur ]0,1[. Si f(1) = 0, alors c = 1 convient car f(c) = f(1) = 0 et f'(c) = f'(1) = 0. Si f(1) > 0, on calcule g(0), g(1) et g'(1). On a g(0) = 0, g(1) = f(1)/1 > 0 et g'(1) = f'(1) - f(1) < 0. On en déduit que g'(x) s'annule sur ]0,1[, ce qui signifie qu'il existe un point c compris entre 0 et 1 où f'(c) = f(c)/c. Si f(1) < 0, on applique le même raisonnement en changeant les signes. On trouve également un point c où f'(c) = f(c)/c. En résumé, dans les conditions données (f(0) = f'(0) = f'(1) = 0), on a démontré qu'il existe un point c dans [0,1] où la corde et la tangente de la fonction f sont confondues.

A- Théorème de Darboux

Le théorème de Darboux affirme que si une fonction f est continue et dérivable sur un intervalle i, alors l'ensemble des taux d'accroissement de f entre deux points de i est un intervalle. Dans cette vidéo, nous allons démontrer ce théorème. Tout d'abord, nous définissons l'ensemble des taux d'accroissement de f entre deux points de i. Cet ensemble représente toutes les valeurs possibles des cordes entre deux points de la fonction. Nous examinerons différents cas pour caractériser les taux de f : si f est injective, croissante, monotone ou elliptique. Si f est injective, cela signifie que pour x différent de y, f(x) est différent de f(y). Par conséquent, f'(x) ne peut pas être égal à f'(y), donc 0 n'appartient pas à l'ensemble des valeurs possibles des taux de f. Si f est croissante, cela signifie que pour x plus petit que y, f(x) est plus petit que f(y). Dans ce cas, les taux d'accroissement seront positifs ou nuls, donc l'ensemble des taux de f est inclus dans les nombres réels positifs. Si f est strictement croissante, les taux d'accroissement ne peuvent pas être nuls, donc l'ensemble des taux de f est également inclus dans les nombres réels positifs. Si f est Lipschitzienne avec une constante k, cela signifie que |f(x) - f(y)| est inférieur à k|x - y|. Dans ce cas, les taux d'accroissement sont compris entre -k et k, ce qui limite les valeurs possibles. Ensuite, nous analysons une expression donnée et nous devons démontrer qu'elle est strictement positive. En utilisant la formule du barycentre, nous montrons que cette expression ne peut pas s'annuler, car elle est formée par des points strictement positifs et des coefficients positifs. Par conséquent, cette expression est toujours supérieure à zéro. Cette propriété nous permet de travailler avec une fonction qui est en réalité un taux d'accroissement entre deux points. Nous pouvons alors appliquer le théorème des valeurs intermédiaires pour montrer que l'ensemble des valeurs prises par le taux de f est inclus dans l'ensemble des valeurs possibles de θ, où θ est une fonction définie sur l'intervalle 0,1. En utilisant la continuité de f et le fait que les coefficients des barycentres sont compris entre 0 et 1, nous montrons que l'ensemble des taux de f contient le segment d'extrémité f(y) - f(x) / y - x, ainsi que f(y') - f(x') / y' - x'. Par conséquent, l'ensemble des taux de f est un intervalle. Ce résumé SEO friendly du cours explique la démonstration du théorème de Darboux qui affirme que l'ensemble des taux d'accroissement d'une fonction continue et dérivable sur un intervalle est un intervalle.

Algèbre

Division euclidienne

Bonjour, je m'appelle Paul et aujourd'hui je vais vous expliquer comment écrire la division euclidienne de -534 par 6. La division euclidienne est représentée par l'équation -534 = 6 * Q + R, où -534 est le dividende, 6 est le diviseur, Q est le quotient (qui peut être positif ou négatif) et R est le reste (qui est un entier compris entre 0 et 6). Pour trouver le quotient et le reste, nous allons effectuer la division. Nous prenons -53 comme premier nombre (en ignorant le signe "-") et nous le divisons par 6. Pour obtenir -53, nous devons multiplier 6 par -8 et ajouter 48. Il reste -5. Nous descendons ensuite le 4 pour obtenir -54 et nous multiplions 6 par -9 pour obtenir -54 également. Il ne reste plus rien, donc le quotient est -89 et le reste est 0. Ainsi, la division euclidienne de -534 par 6 donne -534 = -89 * 6 + 0. Il est important d'inclure le "+ 0" pour indiquer que le reste est effectivement 0. N'oubliez pas de bien comprendre et retenir cette écriture précise de la division euclidienne. Merci et à bientôt !

Algèbre