Cours d'apprentissage en ligne

Tirage successif avec remise

L'exercice consiste à compter le nombre de poignées de mains échangées entre deux équipes de 15 personnes chacune. Pour résoudre ce problème, il est nécessaire d'analyser la nature de la poignée de main. Une poignée de main représente une paire de personnes, une personne de chaque équipe. Ainsi, pour déterminer le nombre de paires possibles, il faut multiplier le nombre de personnes dans chaque équipe. Dans ce cas, il y a 15 possibilités dans l'équipe 1 et 12 possibilités dans l'équipe 2, soit un total de 180 poignées de mains échangées. Il est important de noter que chaque poignée de main est comptée une seule fois, car elles sont répertoriées dans des listes distinctes, en accordant une importance à l'ordre des équipes. Ainsi, le résultat obtenu est sûr et ne compte pas deux fois les mêmes personnes ou poignées de mains. En comprenant clairement ce qui est réellement compté, c'est-à-dire des paires, le problème devient beaucoup plus simple à résoudre.

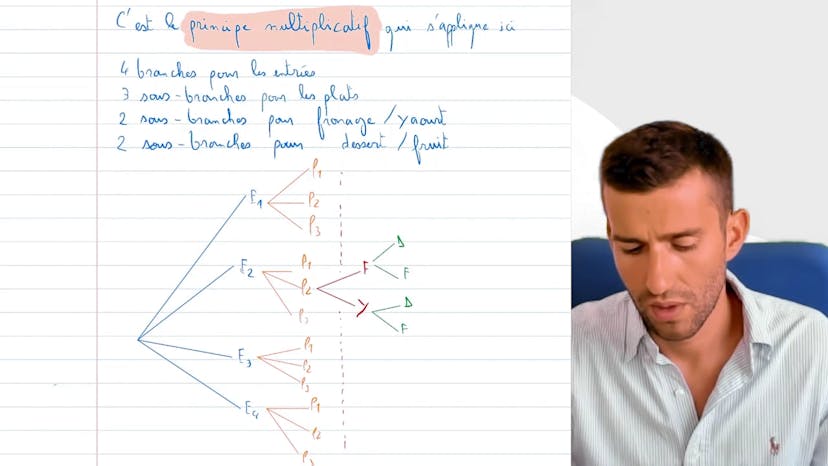
Principe multiplicatif et arbre pondéré

Dans cette vidéo, nous apprenons comment réaliser un arbre pondéré pour dénombrer le nombre de menus possibles dans une cantine scolaire. L'arbre pondéré est une méthode pratique, bien qu'elle demande du temps à réaliser. Il est recommandé de ne pas s'attarder sur cette méthode si le nombre de sous-branches devient trop important. Dans notre exemple, la cantine propose 4 entrées, 3 plats, et le choix entre fromage ou yaourt et entre dessert ou fruit. Pour déterminer le nombre de menus possibles, nous construisons un arbre avec ces différentes options. Cependant, pour simplifier, nous ne représentons pas toutes les combinaisons. En effet, avec 4 entrées, 3 plats, 2 choix de produits laitiers, et 2 choix de desserts ou fruits, cela ferait un total de 48 branches, ce qui devient fastidieux. Pour compter le nombre de menus possibles, nous utilisons le principe multiplicatif. Nous multiplions les possibilités de chaque catégorie : 4 (entrées) x 3 (plats) x 2 (choix de produits laitiers) x 2 (choix de desserts ou fruits), ce qui donne un total de 48 menus possibles. Il est important de noter que dans cet arbre, les pondérations ne sont pas prises en compte. Les pondérations seraient utilisées dans le contexte des probabilités, où différentes probabilités pourraient être attribuées à chaque choix. Cependant, cela ne fait pas partie de cette discussion et sera abordé dans un prochain chapitre.

Exo type en une minute !

Le cours traite d'un petit test comportant quatre questions à choix vrai ou faux. Le candidat répond au hasard et le cours s'intéresse à la probabilité qu'il obtienne toutes les bonnes réponses. Le nombre total de combinaisons possibles est de 2 puissance 4, soit 16. Ainsi, si le candidat répond au hasard, il a une chance sur 16 d'obtenir quatre bonnes réponses. Ce petit test est intéressant car il permet de comprendre les probabilités associées aux réponses au hasard.

Cours par la pratique 1

Aucun résumé n'est disponible pour cette vidéo

Avec et sans ordre de tirage

Dans ce cours, nous cherchons à déterminer le nombre de mains possibles dans un jeu de 32 cartes en utilisant différentes contraintes. Tout d'abord, nous explorons le cas du carré d'As, où 4 cartes sont déjà définies. Il nous reste donc 28 choix possibles pour la dernière carte. Ensuite, nous étudions le nombre de mains possibles avec 5 cartes de la même couleur. Il y a 4 couleurs dans le jeu de cartes, nous devons donc sélectionner 5 cartes parmi les 8 correspondant à une couleur. Le nombre total de mains possibles est donc de 4 fois le nombre de combinaisons de 5 parmi 8. Enfin, nous abordons le cas précis d'une paire exacte. Cela signifie que nous ne voulons pas avoir ni deux paires, ni un brelan. Nous devons donc choisir nos 3 cartes restantes parmi les 30 restantes après avoir fixé la paire. Pour chaque carte restante, nous devons faire attention à ne pas la sélectionner parmi les cartes déjà choisies. Le nombre total de mains possibles est donc obtenu en multipliant les nombres de choix pour chaque carte restante. Il est important de noter que ces calculs doivent être répétés pour chaque hauteur de paire possible (As, Roi, Dame, Valet, 10, 9, 8, 7), ce qui donne un total de 8 choix. Le nombre final de mains possibles est donc obtenu en multipliant ce nombre de choix par le nombre de paires possibles pour chaque hauteur. En résumé, le nombre de mains possibles avec un carré d'As est de 28, le nombre de mains avec 5 cartes de la même couleur est de 4 fois le nombre de combinaisons de 5 parmi 8, et le nombre de mains avec exactement une paire est donné par le produit des nombres de choix pour chaque carte restante, pour chaque hauteur de paire possible.

Permutations : application

Dans cette vidéo, nous apprenons comment gérer les permutations. Une permutation est le nombre de façons de changer l'ordre d'un ensemble ou d'une liste. Par exemple, pour un tirage de loto, combien de façons avons-nous de changer l'ordre des numéros une fois qu'ils sont fixés ? La conférence dont il est question dans cet exemple comprend 12 scientifiques, dont 6 hommes et 6 femmes. Parmi eux, il y a 5 mathématiciens, 3 physiciens et 4 biologistes. Chaque groupe de scientifiques a une méthode différente pour se placer. Nous allons examiner ces méthodes. La méthode des mathématiciens consiste à se placer au hasard. Ils ont donc 12 personnes dont l'ordre doit être défini. Le nombre de permutations pour un ensemble de n éléments est donnée par la formule n!. Dans ce cas, il y a donc 12! = 479 millions de façons de positionner les scientifiques. C'est la méthode la plus aléatoire et qui offre le plus de possibilités, car il n'y a aucune contrainte. La méthode des physiciens est de rester ensemble. Donc les physiciens sont placés côte à côte et les autres scientifiques peuvent se placer librement. Il y a 3 physiciens, qui peuvent être placés de différentes manières. Une fois que la position du premier physicien est fixée, les deux autres suivent automatiquement. Il y a donc 10 positions possibles pour le premier physicien. Ensuite, il y a 6 permutations possibles pour les 3 physiciens. Enfin, il reste 9 places à attribuer aux autres scientifiques, ce qui donne 9! façons de les positionner. En utilisant le principe multiplicatif, il y a donc un total de 10 x 6 x 9! = 21 millions de possibilités. C'est beaucoup moins que la méthode aléatoire précédente car il y a des contraintes. La méthode des biologistes consiste à placer les femmes et les hommes ensemble. Il y a deux façons de placer ces deux groupes. Une fois que ce choix est fait, il y a 6! façons de positionner les femmes et 6! façons de positionner les hommes. En utilisant le principe multiplicatif, il y a donc un total de 2 x 6! x 6! = 1 million 36 800 possibilités. Cela montre comment appliquer le comptage des permutations dans des petits exemples. Si vous avez des questions, n'hésitez pas à consulter la FAQ du cours.

Dénombrer des combinaisons

Les combinaisons sont utilisées lorsque nous avons des ensembles où l'ordre ne compte pas et où il n'y a pas de répétition. Par exemple, au tirage du loto, nous cochons des cases sans ordre spécifique. Dans le jeu de bridge, chaque joueur reçoit une main de 13 cartes parmi un jeu de 52 cartes. Pour déterminer le nombre de mains possibles, nous utilisons la formule "13 parmi 52". Ensuite, pour déterminer le nombre de mains contenant uniquement un cœur, nous devons choisir un cœur parmi les 13 disponibles, puis choisir les 12 cartes restantes parmi les 39 qui ne sont pas des cœurs. La formule utilisée est "12 parmi 39". Il est important de repérer quand utiliser les combinaisons en identifiant les ensembles où l'ordre ne compte pas et où il n'y a pas de répétition.

Combinaison et intersection

Dans cet exemple, nous avons 20 élèves au total, parmi lesquels 14 aiment les maths, 7 aiment la physique et 4 aiment à la fois les maths et la physique. Pour trouver combien de groupes de 4 élèves qui aiment les maths peuvent être formés parmi les sous-groupes possibles, nous utilisons des combinaisons. Nous devons choisir 4 élèves parmi les 14 qui aiment les maths, ce qui donne "14 parmi 4". En simplifiant mathématiquement, nous obtenons 14 x 13 x 12 x 11, soit 1001 possibilités. Puis, pour trouver combien de groupes de 2 élèves qui n'aiment que les maths et 2 élèves qui n'aiment que la physique peuvent être formés parmi les sous-groupes de 4 élèves, nous utilisons également des combinaisons. Il y a 10 élèves qui aiment uniquement les maths et 3 élèves qui aiment uniquement la physique. Nous devons choisir 2 élèves parmi les 10 qui aiment les maths et 2 élèves parmi les 3 qui aiment la physique. En calculant "2 parmi 10" et "2 parmi 3", nous obtenons 2 x 9 x 2 x 1 x 2 x 1, soit 36 possibilités. Ainsi, en combinant les concepts de combinaison et d'intersection, nous avons trouvé qu'il y a 1001 groupes de 4 élèves qui aiment les maths parmi tous les sous-groupes possibles, et 135 groupes de 2 élèves qui n'aiment que les maths et 2 élèves qui n'aiment que la physique parmi les sous-groupes de 4 élèves.

Classique : jetons colorés

Le cours porte sur les méthodes de dénouement en utilisant des jetons de différentes couleurs. Il y a 20 jetons au total, dont 8 blancs avec le numéro 0 et 5 rouges avec le numéro 7. On tire simultanément 4 jetons et on cherche à calculer différentes combinaisons. La première question concerne le nombre de tirages possibles sans répétition. Il suffit de calculer les combinaisons de 4 parmi 20, ce qui équivaut à 4845. Ensuite, on s'intéresse au nombre de tirages avec les quatre numéros identiques. Les seuls numéros qui apparaissent au moins quatre fois sont le 0, le 2 et le 7. On calcule alors les combinaisons de 4 parmi 8 pour le numéro 0, de 4 parmi 5 pour le numéro 2, et de 4 parmi 4 pour le numéro 7. On obtient ainsi 67 possibilités. La troisième question concerne le nombre de tirages avec uniquement des jetons blancs. Il y a 12 jetons blancs au total, donc on calcule les combinaisons de 4 parmi 12, ce qui donne 495. Ensuite, on cherche le nombre de tirages avec des jetons de la même couleur. Il n'y a que le blanc et le rouge qui sont représentés avec plus de 4 jetons. On calcule donc les combinaisons de 4 parmi 12 pour le blanc, et de 4 parmi 8 pour le rouge. On obtient ainsi 565 possibilités. La cinquième question demande de former le nombre 2020 avec les jetons. Comme l'ordre ne compte pas, on considère les possibilités pour chaque numéro. Il y a 8 jetons avec le numéro 2 et 4 jetons avec le numéro 0. On calcule alors les combinaisons de 2 parmi 8 pour le 2, et de 2 parmi 4 pour le 0. On obtient ainsi 268 possibilités. Enfin, la dernière question est un peu plus complexe. On cherche le nombre de tirages qui comportent au moins un jeton avec un numéro différent des autres. On considère alors l'événement contraire, c'est-à-dire des jetons tous identiques. On a déjà calculé qu'il y avait 76 tirages avec les numéros identiques, donc on soustrait ce nombre du total de tirages possible, ce qui donne 4739. Il est important de noter qu'en dénombrement et en probabilité, il est souvent utile de considérer l'événement contraire pour simplifier les calculs.

Entiers dont la somme des chiffres vaut 3

Le cours aborde le problème de déterminer combien de nombres entiers inférieurs à 10^P (puissance P) existent. On commence par remarquer qu'il y en a 10^P + 1, en considérant le 0. Ensuite, on cherche à savoir combien de ces nombres ont une somme de chiffres égale à 3. On utilise des exemples pour comprendre la structure du problème. Pour

Jeu de cartes

Dans cet exercice, nous devons calculer différentes probabilités liées au tirage de cartes d'un paquet de 32 cartes. La première question concerne la probabilité d'obtenir uniquement des cœurs. Il y a 8 cœurs dans le paquet, donc le nombre de tirages possibles pour obtenir que des cœurs est de 3 parmi 8. Le nombre total de tirages est de 3 parmi 32 (car on tire 3 cartes parmi un paquet de 32 cartes). En utilisant la formule de probabilité (nombre d'issues favorables divisé par le nombre d'issues total), nous obtenons la probabilité recherchée qui est de 7 sur 620. Ensuite, nous devons calculer la probabilité d'obtenir uniquement des As. Il y a 4 As dans le paquet, donc le nombre de tirages possibles pour obtenir que des As est de 3 parmi 4. En utilisant la même formule de probabilité, nous obtenons la probabilité recherchée qui est de 1 sur 1240. Enfin, la dernière question concerne la probabilité d'obtenir 2 cœurs et 1 pic. Pour cela, nous devons compter séparément le nombre de tirages possibles pour obtenir 2 cœurs (2 parmi 8) et pour obtenir 1 pic (1 parmi 8). En multipliant ces deux nombres, nous obtenons le produit 7 fois 4 fois 8. Le nombre total de tirages reste le même que précédemment, soit 3 parmi 32. En simplifiant les factorielles, nous obtenons la probabilité recherchée qui est de 7 sur 155. C'est ainsi que se conclut cet exercice de probabilité lié au tirage de cartes.