Cours d'apprentissage en ligne

Noyau et image par la matrice

Dans cette transcription de la vidéo, le professeur explique des techniques et astuces pour résoudre des problèmes mathématiques liés aux matrices et aux applications linéaires. Il propose une méthode classique pour trouver le noyau d'un endomorphisme F2R3 à partir d'une matrice donnée. Cette méthode consiste à résoudre un système d'équations linéaires en prenant un vecteur XYZ et en le substituant dans le produit matriciel AX pour obtenir AX = 0. En résolvant ce système, on peut trouver un ou deux vecteurs du noyau. Ensuite, le professeur montre comment déterminer l'image de manière plus simple en utilisant des combinaisons linéaires. Il suffit d'écrire que l'image est le vecteur F2E1, F2E2, F2E3 et de simplifier cette expression en trouvant des relations linéaires entre les variables. Il explique également comment utiliser le théorème du rang pour déterminer rapidement le noyau et l'image. En trouvant le noyau en premier et en utilisant ce résultat pour déterminer l'image, on évite de résoudre un système. Le professeur donne un exemple concret où il trouve le noyau d'une matrice et l'image en utilisant les techniques qu'il a expliquées. Il montre comment réécrire le vecteur XYZ en fonction d'une seule variable, et comment utiliser cette relation pour trouver le noyau. Ensuite, il utilise le théorème du rang et un lemme pratique pour déterminer l'image en trouvant deux vecteurs indépendants parmi les trois. En conclusion, le professeur explique que travailler avec les dimensions lui permet d'éviter des calculs laborieux et simplifie la résolution des problèmes. Il encourage les étudiants à poser des questions en cas de besoin.

Techniques Rapides !

Dans cette vidéo, l'enseignant explique comment résoudre un exercice où il faut trouver le noyau et l'image d'une matrice sans utiliser les méthodes classiques. Il utilise une approche basée sur l'observation minutieuse de la matrice et la recherche de combinaisons linéaires intelligentes. D'abord, il observe que la matrice a un rang d'au moins 2 car il trouve deux vecteurs non parallèles. Il cherche à différencier les cas où le rang est 2 ou 3. S'il peut trouver une combinaison linéaire entre les trois vecteurs, cela signifierait qu'ils sont dépendants et donc le rang est 2. Pour cela, il se concentre sur un 0 dans la matrice et utilise cette information pour trouver une combinaison linéaire intelligente entre les vecteurs. En utilisant cette technique, il trouve une combinaison linéaire entre les deux premiers vecteurs qui est égale au troisième vecteur. Cela montre que le rang de la matrice est inférieur ou égal à 2. Étant donné que les deux premiers vecteurs sont indépendants, il peut conclure que l'image de la matrice est l'espace vectoriel engendré par ces deux vecteurs. Ensuite, il utilise le fait qu'il a trouvé une combinaison linéaire pour trouver le noyau de la matrice. En utilisant le théorème du rang, il sait que le noyau a une dimension de 1. Il trouve un vecteur dans le noyau en utilisant la combinaison linéaire précédente et conclut que le noyau de la matrice est l'espace vectoriel engendré par ce vecteur. En résumé, en observant minutieusement la matrice et en trouvant des combinaisons linéaires intelligentes, l'enseignant parvient à déterminer l'image et le noyau de la matrice sans utiliser les méthodes classiques. Cette approche demande de la pratique et une bonne compréhension du théorème du rang.

Matrices de Matrices !

Dans cet exercice, nous étudions une application F définie par F(M) = AM, où A est une matrice fixée. Il est important de noter qu'il ne s'agit pas de F associée à la matrice A, mais plutôt d'une application linéaire d'un espace de dimension 4 à lui-même. Pour montrer que F est linéaire, on utilise les règles de linéarité du produit matriciel. En prenant M et N comme éléments de M22R (matrices de dimension 2x2 ayant des éléments réels), et lambda et mu comme constantes réelles, on obtient F(lambdaM + muN) = lambdaAM + muAN, ce qui prouve la linéarité de F. Ensuite, pour déterminer la matrice de F dans la base canonique de M22R, on considère les éléments de base E1 1, E1 2, E2 1 et E2 2. On calcule F(E1 1), F(E1 2), F(E2 1) et F(E2 2) en multipliant chaque élément par A. En regroupant ces résultats dans une matrice 4x4, on obtient la matrice de F dans la base canonique. Il est important de noter que l'ordre dans lequel les éléments de base sont rangés peut varier, mais généralement, dans le cas de la base canonique, l'ordre est E1 1, E2 1, E1 2 et E2 2. J'espère que cette explication était claire. À bientôt pour une prochaine vidéo.

Inverse de matrice

Le cours porte sur plusieurs notions en mathématiques, notamment la détermination du noyau et de l'image d'une application linéaire, ainsi que le calcul de puissances d'une matrice. L'auteur utilise une matrice spécifique, notée F, pour illustrer ces concepts. Dans un premier temps, l'auteur propose de calculer les puissances M² et M³ de la matrice F. Ensuite, il s'intéresse aux images et aux noyaux de M² et F². Pour cela, il utilise l'observation et la combinaison linéaire des vecteurs de la matrice. Ensuite, l'auteur utilise une méthode alternative en utilisant une matrice de passage associée à l'application linéaire F. Il calcule les composantes des vecteurs de base E1, E2 et E3 après l'application de F. Il en déduit l'image de F et le noyau de F. Dans la suite du cours, l'auteur explique qu'il est possible de prédire que la puissance M³ pourrait être nulle, mais il effectue quand même le calcul pour confirmer ce résultat. Il conclut en donnant des astuces pour certains calculs, notamment lorsque l'on a des polynômes comme 1-x². Enfin, l'auteur recommande de s'entrainer sur ce genre d'exercices pour mieux comprendre les liens entre application linéaire et matrice. Il encourage également les questions et les échanges pour approfondir ces concepts mathématiques.

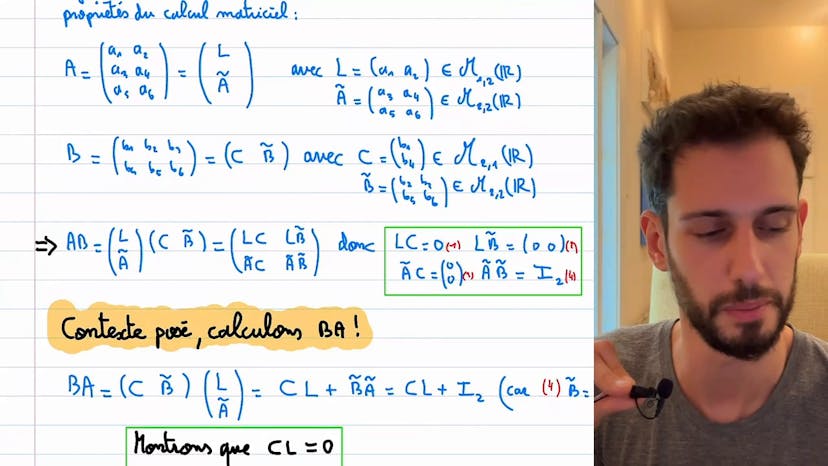
D’un produit à l’autre

Le cours explique une méthode pour résoudre un exercice de matrices de manière élégante. Les matrices A et B sont définies avec des dimensions spécifiques, et il est demandé de démontrer que le produit BA est égal à la matrice identité. La méthode utilisée consiste à visualiser les matrices comme des blocs et à multiplier les blocs de lignes et de colonnes ensemble pour rendre les calculs plus globaux. Les matrices A et B sont donc décomposées en blocs A1, A2 et A tilde, ainsi que B1, B tilde respectivement. En utilisant cette notation, le produit AB est calculé comme la multiplication de LA, A tilde, C et B tilde. En faisant cette multiplication, on obtient L fois C, L fois B tilde, A tilde fois C et A tilde B tilde. En utilisant les informations données, on déduit que L fois C et L fois B tilde sont nuls, A tilde fois C est nul et A tilde B tilde est égal à la matrice identité I2. Le produit BA est ensuite calculé de manière similaire, donnant CL plus I2. Puisque A tilde B tilde est égal à I2, on peut conclure que CL est égal à 0, et donc que BA est égal à la matrice identité. Cette méthode utilise la vision des matrices comme des blocs et permet des calculs plus efficaces.

Matrice d’une rotation

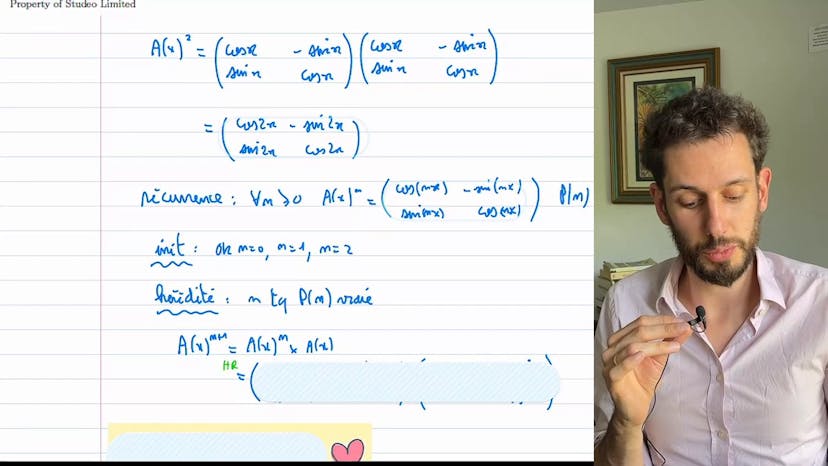
Dans ce cours, on étudie une puissance n d'une fonction a2x = cos(x) - sin(x). On utilise une méthode en deux temps : d'abord, on essaye avec de petites valeurs de n, puis on utilise la récurrence pour généraliser. On begin par calculer a2x, qui donne cos(2x) - sin(2x). En remarquant que cos(2x) = cos²(x) - sin²(x) et que sin(2x) = 2sin(x)cos(x), on peut réécrire a2x comme cos²(x) - sin²(x) - (2sin(x)cos(x)). On peut généraliser cette forme pour a2n en utilisant la récurrence avec cosnx - sinnx. On fait une initialisation pour n=0, n=1 et n=2 pour montrer que la récurrence est vraie. Ensuite, on montre que la récurrence est vraie pour n+1 en utilisant les formules cos(a+b) et sin(a+b). On obtient alors cos(n+1)x - sin(n+1)x. Pour les valeurs de n entiers négatifs, on calcule d'abord a-1(x) en utilisant l'inverse de la matrice 2x2 associée à cos(x) - sin(x). On obtient que l'inverse de a2x est la transposée de a2x. En utilisant les propriétés de la transposée et des puissances, on montre que a-n(x) = (a-1(x))^n, ce qui donne la même forme que pour les valeurs de n positives avec un signe moins à un autre endroit. En résumé, on a trouvé une relation générale pour la puissance n de la fonction a2x = cos(x) - sin(x) en utilisant la récurrence et en montrant que cela fonctionne aussi pour les valeurs de n entiers négatifs.

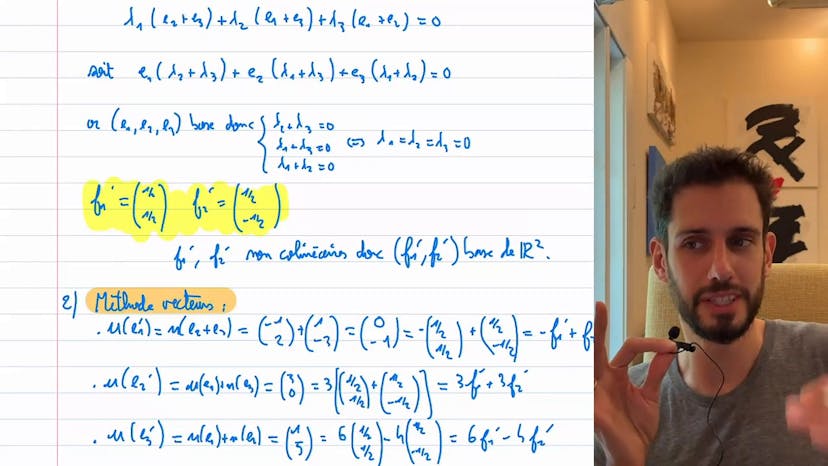
Changement de base

Dans ce cours, nous étudions une application linéaire de R3 dans R2. Nous voulons montrer que les bases E1', E2', E3' et F1', F2' sont libre pour R3 et R2 respectivement. Afin de montrer la liberté de ces vecteurs, nous les combinons de manière appropriée pour prouver que les coefficients correspondants sont nuls. De plus, nous montrons que F1' et F2' sont indépendants puisqu'ils ne sont pas collinaires. Ensuite, nous cherchons la matrice de l'application linéaire U dans ces nouvelles bases. Pour cela, nous exprimons U(E1'), U(E2'), et U(E3') en termes de F1' et F2'. En utilisant la définition de U dans la base canonique, nous calculons ces expressions dans la base canonique avant de les réécrire dans la base F1, F2. Ensuite, nous essayons différentes combinaisons linéaires de F1' et F2' pour exprimer les résultats dans la base F1', F2'. En résolvant un système ou en faisant des essais, nous trouvons les coefficients appropriés. Finalement, nous obtenons la matrice de U dans les nouvelles bases en utilisant les expressions trouvées. Il est recommandé de faire ces calculs mentalement, mais il est également possible de poser des systèmes d'équations pour obtenir les coefficients.

Matrices semblables

Ce cours explique comment déterminer si les matrices A, B, C et D sont semblables. Plutôt que de tenter de trouver une matrice P telle que B = P-1 A P, on utilise l'application linéaire associée, notée F. On cherche une base (E1, E2, E3) telle que F(E1) = 0, F(E2) = E3 et F(E3) = 0. On peut réorganiser la base si nécessaire. Par exemple, pour la matrice B, on peut observer F dans la base (E2, E3, E1) au lieu de (E1, E2, E3). On choisit alors U1 = E1, U2 = E3 et U3 = E2. On vérifie que F(U1) = 0, F(U2) = E2 et F(U3) = 0, ce qui correspond bien à la matrice B. Les mêmes étapes sont appliquées pour les matrices C et D. Pour C, on choisit la base (V2, V3, V1) avec V1 = E2, V2 = E3 et V3 = E1. Pour D, on choisit la base (W2, W3, W1) avec W1 = 4E3, W2 = E2 et W3 = E1. Ainsi, en comprenant les matrices comme représentant des applications linéaires, on peut déterminer si elles sont semblables en utilisant cette méthode.

Matrice de passage

Le cours traite de l'endormorphisme U défini à partir d'une base canonique et de trois vecteurs w1, w2, w3. La matrice de cet endomorphisme est calculée en fonction de ces vecteurs. Ensuite, le cours aborde la détermination d'une base du noyau et de l'image de U, ainsi que la détermination du noyau et de l'image de l'endomorphisme U - Id, où Id est l'identité. Il est démontré que U - Id est bijective, ce qui le qualifie d'automorphisme. Enfin, le cours conclut que le noyau de cet automorphisme est réduit à zéro, ce qui signifie qu'il est inversible.

Changement de base

Aucun résumé n'est disponible pour cette vidéo

Matrices triangulaires

Ce cours traite de deux résultats sur les matrices triangulaires. Le premier résultat démontre que pour qu'une matrice triangulaire supérieure soit inversible, tous ses coefficients diagonaux doivent être non-nuls. Le deuxième résultat montre que toute matrice triangulaire supérieure peut être rendue semblable à une matrice triangulaire inférieure. Pour démontrer ces résultats, l'auteur utilise des méthodes de contraposée et de changement de base. Il explique en détail les étapes à suivre pour parvenir à ces conclusions. En utilisant des termes simples et des exemples concrets, l'auteur rend le cours facile à comprendre. Ce cours est une transcription d'une vidéo d'enseignement.