 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Prépa Examens
Concours et examens UK
Terminale

Résoudre x = aˣ, et en moins de 10 minutes
Bonjour à tous ! Aujourd'hui, je vais résumer en utilisant des termes SEO-friendly un cours qui est une transcription d'une vidéo. Dans ce cours, nous allons aborder un exercice qui est tombé à Cambridge en 2014. Cet exercice ressemble à un exercice d'analyse de fonctions qui peut être réalisé en Terminale, grâce aux outils que nous utilisons régulièrement. L'énoncé nous demande de démontrer que l'équation x égale a puissance x n'a aucune racine réelle si a est strictement supérieur à e puissance 1 sur e. Nous supposons que a est positif pour simplifier les calculs. Ensuite, nous déduisons que x doit également être positif pour éviter une contradiction. Pour résoudre cette équation, nous prenons le log de chaque côté pour simplifier les calculs. En dérivant, nous étudions les variations de la fonction f et trouvons son maximum. En analysant les limites de la fonction, nous déterminons les conditions pour lesquelles elle a des racines réelles ou non. Finalement, nous concluons que si a est strictement supérieur à e puissance 1 sur e, l'équation n'a pas de racines réelles, et si a est strictement inférieur à 1, l'équation a une unique racine réelle. J'espère que cette résumé SEO-friendly vous a aidé à comprendre le contenu du cours. N'hésitez pas à vous abonner à la chaîne pour plus de vidéos et de conseils mathématiques. À bientôt !
Prépa Examens
Concours et examens UK
Terminale

Des puissances 100 et plus ?
Dans cet exercice, on nous donne une suite récurrente définie par a1 = 3 et an+1 = an^3 pour n ≥ 1. On nous demande de trouver le chiffre des unités pour le nombre a7, de montrer que a7 ≥ 10^100, et de déterminer la valeur de (a7 + 1) / (2a7) avec une précision de deux décimales.
Pour la première question, on analyse la suite et on remarque que les chiffres des unités alternent entre 7 pour les indices pairs et 3 pour les indices impairs. Donc le chiffre des unités pour a7 est 3.
Pour la deuxième question, on utilise la formule explicite de an = 3^n-1 et on montre que a7 = 3^(3^6) qui est beaucoup plus grand que 10^100. Donc a7 ≥ 10^100.
Pour la troisième question, on écrit (a7 + 1) / (2a7) = 1/2 + 1/(2a7) et on constate que 1/(2a7) est beaucoup plus petit que 0,0001. Donc, à deux décimales près, la valeur de (a7 + 1) / (2a7) est 0,50.
En conclusion, le chiffre des unités pour a7 est 3, a7 est plus grand ou égal à 10^100, et (a7 + 1) / (2a7) est environ égal à 0,50.
Prépa Examens
Concours et examens UK
Terminale

1, et 2, et… 4 valeurs absolues !
Dans cette vidéo, nous avons un exercice de mathématiques qui consiste à trouver toutes les solutions d'une équation. L'exercice se décompose en plusieurs étapes. Tout d'abord, nous devons comprendre qu'il s'agit d'un exercice où la précision et l'efficacité sont requises, plutôt que la créativité. Ensuite, nous différencions les différentes valeurs absolues selon les intervalles donnés. Nous combinons ensuite ces valeurs absolues pour obtenir une expression pour f(x). Ensuite, nous essayons de résoudre l'équation f(2x) = x + 2 sur chaque intervalle en vérifiant que les solutions obtenues sont valides pour chaque intervalle. L'équation a une solution valide sur l'intervalle -∞ à -1 et sur l'intervalle 1 à +∞. En revanche, il n'y a pas de solution valide sur les intervalles -1 à 0 et 0 à 1. Ainsi, la solution de l'équation est l'ensemble des réels entre 2 et +∞, inclus, ainsi que la solution unique -2. La vidéo conclut en encourageant les spectateurs à poser des questions et à partager d'autres solutions élégantes.
Prépa Examens
Concours et examens UK
Terminale

4 questions en une
Dans cet exercice de Cambridge, nous devons répondre à quatre questions en une. La première question concerne les puissances de logarithmes. L'auteur nous rappelle de toujours appliquer le logarithme lorsque nous avons une puissance complexe. Dans ce cas, nous devons vérifier si a puissance log de b est égale à b puissance log de a pour tout a et b positifs. Après avoir vérifié que a est positif, nous appliquons le logarithme des deux côtés et obtenons log a puissance log b égal à log b puissance log a. En simplifiant, nous trouvons log b multiplié par log a égal à log a multiplié par log b, ce qui est vrai. Donc, la première affirmation est vraie.
La deuxième question concerne les fonctions trigonométriques. On nous demande de vérifier si cos sin θ est égal à sin cos θ pour tout θ réel. Intuitivement, nous pouvons sentir que cette affirmation est fausse et nous pouvons la vérifier en utilisant un contre-exemple. En prenant θ égal à π sur 2, nous pouvons voir que cos sin π sur 2 est égal à cos 1, qui est différent de 0, tandis que sin cos π sur 2 est égal à sin 0, qui est égal à 0. Donc, cette affirmation est fausse.
La troisième question concerne un polynôme P. On nous demande s'il existe un polynôme P tel que P(θ) - cos(θ) soit inférieur ou égal à 10 puissance -6 pour tout θ. Nous pouvons intuitivement sentir
Prépa Examens
Concours et examens UK
Terminale

Dériver 1, 2, ... 3 fois !!
Dans cet exercice, nous étudions une fonction complexe, F2x, ainsi que d'autres fonctions F, G et H qui augmentent en difficulté. Nous devons démontrer différentes propriétés de ces fonctions, telles que leur positivité sur certains intervalles.
Tout d'abord, nous examinons la fonction F et remarquons qu'elle est strictement croissante sur l'intervalle [0, +∞), car sa dérivée est positive ou nulle. En utilisant cette propriété, nous montrons que F2x est positif ou nul pour tout x positif, ce qui répond à la première question.
Ensuite, nous passons à la fonction G et effectuons des calculs similaires pour montrer qu'elle est également positive sur l'intervalle [0, π/2). En dérivant deux fois, nous prouvons que la dérivée seconde de G est positive sur cet intervalle, ce qui implique que la dérivée première de G est croissante et que G est positive.
Nous répétons cette procédure pour la fonction H et démontrons qu'elle est positive sur l'intervalle [0, π/4). En dérivant plusieurs fois, nous constatons que la dérivée troisième de H est positive, ce qui entraîne une croissance stricte de la dérivée seconde de H et donc une positivité de H.
Enfin,
Prépa Examens
Concours et examens UK
Terminale

Une suite avec un produit infini !
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens UK
Terminale
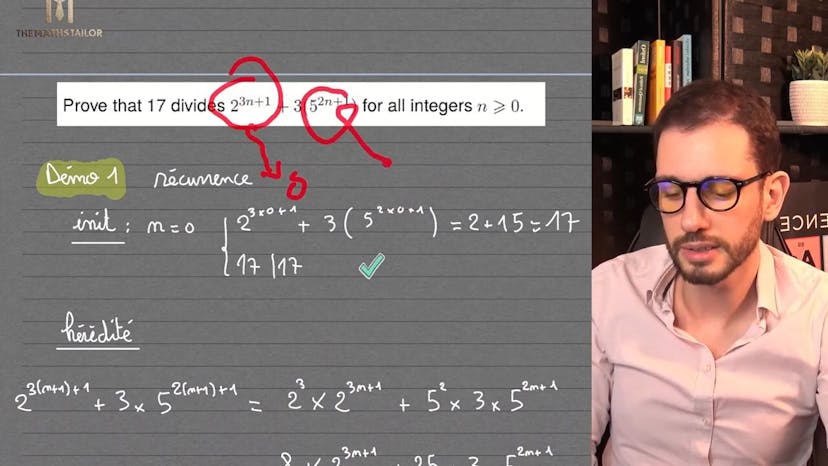
3 démos d'arithmétique de terminale !
Dans cette vidéo, le professeur présente trois démonstrations pour résoudre un exercice d'arithmétique. Il explique que la première méthode consiste à utiliser la récurrence, en montrant que l'expression est divisible par 17 pour n=0 et en faisant apparaître le terme n+1 dans l'expression. La deuxième démonstration utilise les tables de congruence, mais elle se révèle trop longue et complexe pour cet exercice. Finalement, le professeur propose une troisième méthode plus efficace, qui consiste à séparer les termes en puissance n dans l'expression et à remarquer que 8 et 25 sont séparés d'une distance de 17. Ainsi, en utilisant les congruences, il démontre que l'expression est congrue à 0 modulo 17. Il conclut en encourageant les élèves à poser des questions et en annonçant une prochaine vidéo.
Prépa Examens
Concours et examens UK
Terminale
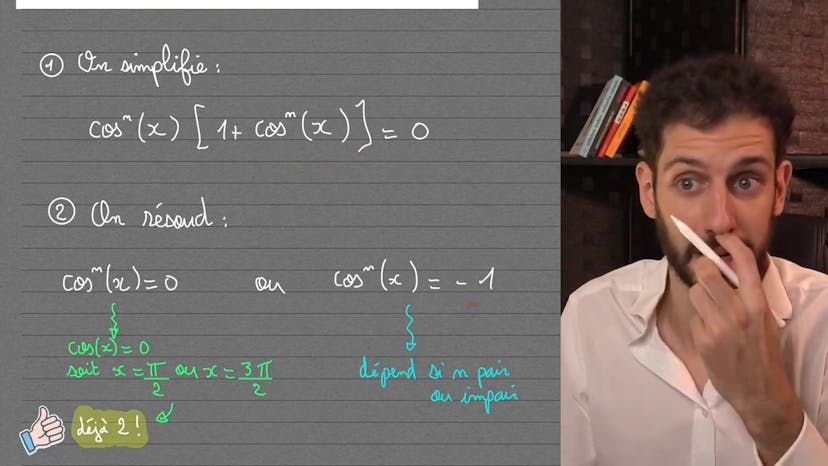
cosⁿ(x) et du sinⁿ(x) dans une équation ?
Le cours traite de la résolution d'une équation et de la trigonométrie. L'exercice consiste à déterminer le nombre de solutions d'une équation donnée. On factorise l'équation et on obtient deux termes possibles : cosinus puissance n de x = 0 et 1 + cosinus puissance n de x = 0. On résout ces équations en fonction des valeurs de n. Pour cosinus puissance n de x = 0, on obtient deux solutions : pi/2 et 3pi/2. Pour 1 + cosinus puissance n de x = 0, on détermine si cela peut être égal à -1 en fonction de la parité de n. Si n est pair, cela n'est pas possible, donc on ne retient pas ces solutions. Si n est impair, cela est possible et on obtient une solution : x = pi. Donc, si n est impair, il y a trois solutions, sinon il y en a deux. Ainsi, on démontre que la réponse est D ou E. Cette stratégie permet de gagner du temps lors de l'examen.
Prépa Examens
Concours et examens UK
Terminale

Produit (et non somme) des termes d'une suite géométrique
Dans cette transcription d'une vidéo, l'auteur explique un exercice de mathématiques issu du Math Admission Test d'Oxford en 2016. Il s'agit de trouver le produit des 15 premiers termes d'une suite géométrique. L'auteur explique la méthode pour trouver la formule générale de cette suite et ensuite il calcule le produit en utilisant une formule connue des suites arithmétiques. La réponse est donc l puissance 105. L'auteur avertit qu'il y a plusieurs questions de ce type dans le concours et conseille de bien maîtriser ce genre d'exercice pour réussir le concours d'entrée en faculté.
Prépa Examens
Concours et examens UK
Terminale
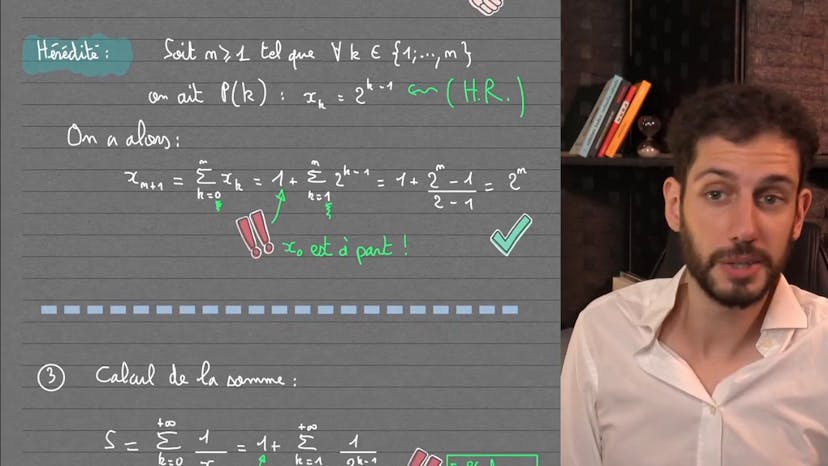
Une somme… d'inverses… de sommes !
Dans cette vidéo, l'enseignant propose de résoudre un exercice tombé à l'université d'Oxford en 2016. Il explique que même si les termes utilisés peuvent sembler complexes, il est possible de les comprendre avec de la méthode et de l'analyse.
Il commence par décoder le problème et expliquer la notion d'une suite définie par des sommes successives. En calculant les premiers termes de la suite, il remarque une certaine régularité qui l'amène à formuler une hypothèse sur le calcul de xn.
En utilisant la récurrence, il vérifie cette hypothèse et démontre que xn est égal à 2 puissance n moins 1. Il précise cependant qu'il faut faire attention à exclure x0 de cette formule, car elle ne s'applique qu'aux indices de 1 à n.
Ensuite, il explique comment calculer la somme demandée. Il insiste sur l'importance de sortir x0 de la somme et de bien comprendre que l'expression précédente ne s'applique qu'aux indices de 1 à n. En utilisant la formule de la somme géométrique, il obtient finalement une réponse de 3.
En conclusion, il souligne l'importance de bien traduire les termes de l'exercice, de comprendre les premiers termes de la suite et d'appliquer les connaissances sur x0. Il encourage les étudiants à poser des questions et se dit prêt pour la prochaine vidéo.
Prépa Examens
Concours et examens UK
Terminale

Une fonction trigo bien moche !
Bonjour à tous ! Dans cette vidéo, nous allons analyser une question du Math Admission Test d'Oxford en 2020. La question est la suivante : "Quelle est la plus grande valeur atteinte par l'expression 3 cos²x plus sin²x plus 1 ?".
La première étape consiste à simplifier l'expression. Pour cela, nous allons utiliser une relation fondamentale de la trigonométrie qui nous dit que cos²x équivaut à 1-sin²x. En remplaçant cos²x par cette équation, nous obtenons l'expression 3-3sin²x plus 2sin²x plus 1, que nous simplifions pour obtenir 3-sin²x plus 2sin²x plus 4.
Nous remarquons qu'il y a un polynôme du second degré caché dans cette expression. Pour faciliter les calculs, nous posons une variable intermédiaire grand x égale à sin²x. Nous notons également que grand x doit être compris entre -1 et 1.
Ainsi, nous avons une nouvelle expression Q2x égale à -3 fois grand x² plus 2x plus 4. Nous devons déterminer la valeur maximale atteinte par cette fonction. Comme il s'agit d'un polynôme du second degré, nous savons qu'elle atteint son maximum. En utilisant la formule du maximum d'un polynôme du second degré, nous trouvons que le maximum est atteint en 1/3.
Nous pouvons calculer la valeur maximale en substituant 1/3 à x dans l'expression Q. Après les calculs, nous obtenons que Q de 1/3 est égal à 13/3.
Ainsi, la réponse à la question est 13/3. J'espère que ce résumé était clair et n'hésitez pas à poser des questions dans les commentaires. À bientôt pour une prochaine vidéo !
Prépa Examens
Concours et examens UK
Terminale
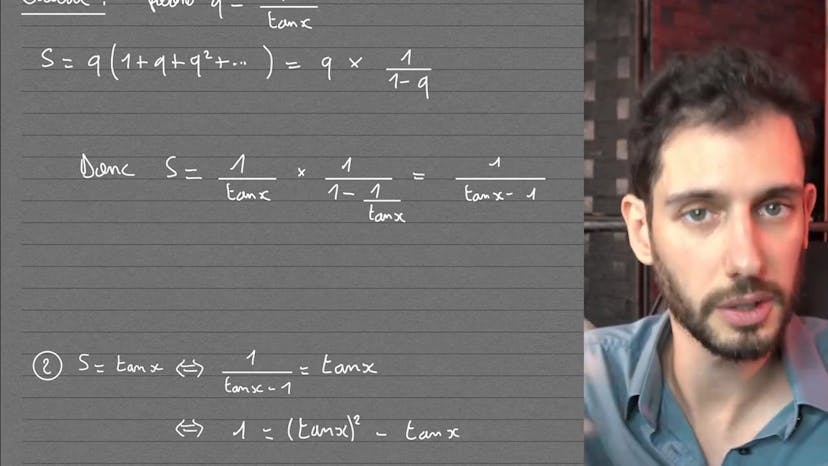
Une suite géométrique !
Bonjour à tous, je m'appelle Antonin et je suis professeur particulier de mathématiques, spécialisé dans les examens d'entrée à l'université d'Oxford. Aujourd'hui, je vais vous présenter un exercice qui est tombé à Oxford en 2020.
L'énoncé demande combien de valeurs de l'angle x, situées entre -90° et 90°, permettent d'égaliser la somme infinie de 1/tangente(x) + 1/tangente^2(x), etc., à la tangente(x).
Pour résoudre cet exercice, on doit tout d'abord comprendre que la fonction tangente(x) est strictement croissante entre -π/2 et π/2. On remarque également qu'on a une série de nombres élevés à des puissances croissantes. Cela nous indique qu'il s'agit d'une somme géométrique.
Notre objectif est de simplifier cette somme et de trouver quand elle est égale à la tangente(x). La première étape consiste donc à simplifier la somme géométrique. Nous savons que cette somme converge si la valeur absolue de la raison (1/tangente(x)) est inférieure à 1. Ainsi, nous devons vérifier que la tangente(x) est strictement supérieure à 1 ou strictement inférieure à -1.
Ensuite, nous pouvons calculer la somme géométrique en utilisant la formule Q/(1-Q), où Q est égal à 1/tangente(x). En remplaçant Q par sa valeur, nous obtenons S = 1/tangente(x) - 1.
Enfin, nous devons résoudre l'équation tangente(x) = S. En posant Y = tangente(x), nous obtenons l'équation 1 = Y^2 - Y. En analysant cette équation, nous trouvons les valeurs de Y satisfaisant la condition d'équivalence.
Après avoir vérifié que les solutions respectent la condition de valeur absolue supérieure à 1, nous trouvons une seule solution acceptable pour tangente(x) : 1 + racine de 5/2.
En conclusion, il y a une seule valeur de l'angle x, située entre -π/2 et π/2, qui satisfait l'équation tangente(x) = 1 + racine de 5/2.
J'espère que cette explication était claire et utile. Les problèmes du MIT et du Math Admissions Test d'Oxford ne sont pas simples, mais avec une bonne décomposition et l'application de ce que nous avons appris en première et en terminale, nous pouvons trouver des solutions. La réponse à cet exercice serait donc la réponse b.


