 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Physique-Chimie
Chimie
MPSI/PCSI
Diastéréoisomères
Dans cette vidéo, nous analysons les différences de propriétés physiques entre deux diastéréoisomères : l'acide Z-butanedioïque et l'acide E-butanedioïque. Nous devons expliquer deux observations expérimentales : la température de fusion inférieure de l'acide Z-butanedioïque par rapport à son diastéréoisomère E, et la solubilité plus élevée de l'acide Z-butanedioïque dans l'eau.
Pour comprendre ces différences, nous devons d'abord examiner ce qui se passe lors de la fusion d'un composé. Lors du passage de l'état solide à l'état liquide, les liaisons entre les molécules doivent être rompues, ce qui nécessite de l'énergie. Plus les interactions entre les molécules sont fortes, plus il faut d'énergie pour les rompre, ce qui se traduit par une température de fusion élevée.
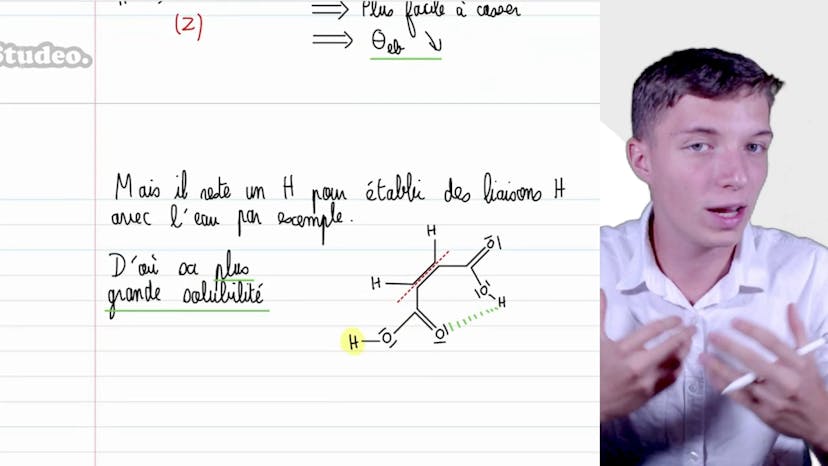
En représentant les molécules de chaque diastéréoisomère selon la représentation de Lewis, nous pouvons voir que l'acide E-butanedioïque présente une double liaison hydrogène entre l'oxygène impliqué dans la double liaison avec le carbone, et l'hydrogène du groupe acide carboxylique de l'autre molécule. Ces liaisons hydrogène intermoléculaires créent des interactions très fortes entre les molécules du composé E, ce qui demande beaucoup d'énergie pour les rompre et entraîne une température de fusion élevée.
En revanche, dans l'acide Z-butanedioïque, les groupements carboxyliques sont disposés du même côté de la molécule, ce qui permet la formation d'une liaison hydrogène intramoléculaire entre l'oxygène de la double liaison et l'hydrogène voisin. Bien que cette liaison hydrogène soit de la même force que dans le composé E, elle est intramoléculaire et ne forme pas d'interactions aussi fortes avec les molécules environnantes. Cela diminue les interactions entre les molécules du composé Z, ce qui rend la rupture des liaisons plus facile et conduit à une température de fusion plus basse.
En ce qui concerne la solubilité dans l'eau, nous pouvons noter qu'il reste un hydrogène non impliqué dans une liaison hydrogène dans l'acide Z-butanedioïque, ce qui lui permet de former des liaisons hydrogène avec les molécules d'eau. En revanche, tous les hydrogènes de l'acide E-butanedioïque sont déjà engagés dans des liaisons hydrogène intramoléculaires. Par conséquent, l'acide Z-butanedioïque se solubilise plus facilement dans l'eau grâce à la formation de liaisons hydrogène supplémentaires avec l'eau.
En résumé, les différences de propriétés physiques entre les diastéréoisomères peuvent être expliquées par leur structure moléculaire et les interactions qui en découlent. Ces facteurs déterminent la température de fusion et la solubilité de ces composés.
Physique-Chimie
Chimie
MPSI/PCSI

Polarisabilité
La polarisabilité des molécules est une grandeur physique qui mesure l'aptitude d'un nuage électronique à se déformer sous l'effet d'un champ électrique. Plus le nuage électronique est éloigné du noyau atomique, plus la polarisabilité est grande.
Dans cette vidéo, nous devons commenter l'évolution des volumes de polarisabilité alpha prime en 10-30 m3 des halogènes et des ions halogénures. Pour les halogènes, lorsque le numéro atomique principal augmente, le nuage électronique s'éloigne du noyau, ce qui augmente la polarisabilité. Cependant, au sein d'une même période, lorsque le numéro atomique z augmente, le noyau devient plus gros et attire davantage les électrons du nuage électronique, ce qui diminue la polarisabilité.
Pour les ions halogénures, l'ajout d'un électron augmente la taille du nuage électronique, ce qui augmente également la polarisabilité.
En ce qui concerne les gaz rares, au sein d'une même famille, le volume de polarisabilité augmente car les couches électroniques deviennent de plus en plus éloignées du noyau.
Il est important de comprendre l'évolution du nuage électronique en se déplaçant dans le tableau périodique pour comprendre l'évolution de la polarisabilité. On peut raisonner en se fixant soit sur une colonne, soit sur une ligne.
En résumé, la polarisabilité des molécules dépend de la distance entre le nuage électronique et le noyau atomique. Lorsque le nuage électronique est éloigné du noyau, la polarisabilité est grande, et inversement. L'ajout d'électrons augmente la taille du nuage électronique, ce qui augmente également la polarisabilité. Dans les gaz rares, les couches électroniques sont de plus en plus éloignées du noyau, ce qui entraîne une augmentation de la polarisabilité.
Physique-Chimie
Chimie
MPSI/PCSI

Liaison hydrogène
La vidéo traite de la liaison hydrogène et de son importance dans les interactions intermoléculaires. Il est crucial de savoir repérer les atomes pouvant participer à une liaison hydrogène dans les molécules de paracétamol. Une liaison hydrogène se forme entre le doublé non liant d'un atome très électronégatif et un atome d'hydrogène lié à un atome très électronégatif. Les molécules d'eau sont propices aux liaisons hydrogènes car elles contiennent à la fois l'atome d'oxygène très électronégatif et l'atome d'hydrogène lié à un atome très électronégatif. Dans la molécule de paracétamol, les atomes d'oxygène, d'azote et l'hydrogène relié à l'oxygène peuvent participer à des liaisons hydrogènes avec l'eau. Il est important de maîtriser cette notion de liaison hydrogène pour analyser les propriétés physico-chimiques des composés.
Physique-Chimie
Chimie
MPSI/PCSI

Longueur et moment
Dans cette vidéo, on étudie la longueur des liaisons hydrogènes entre différentes molécules. On commence par le fluorure d'hydrogène cristallin, où la distance entre deux atomes de fluor est de 249 picomètres et la liaison covalente HF est de 92 picomètres. En déduisant la longueur de la liaison hydrogène HF entre deux molécules différentes, on trouve 157 picomètres.
Ensuite, on se penche sur la molécule d'eau. On compare la liaison hydrogène précédente à celle observée dans la glace, où la distance entre deux atomes d'hydrogène est de 276 picomètres. On suppose que la longueur de la liaison covalente O-H est la même dans la glace et dans la molécule d'eau liquide, qui a un moment dipolaire de 1,84 Debye et un pourcentage ionique de 32%. Dans la molécule d'eau liquide, l'angle HO-H est de 104,5°.
Pour trouver la longueur de la liaison hydrogène dans la molécule d'eau, on utilise la formule du moment dipolaire, qui fait intervenir une longueur particulière L1. On décompose le moment dipolaire global en deux moments distincts (P1 et P2) pour chaque liaison polarisée. En utilisant les valeurs données, on obtient que la longueur de la liaison hydrogène dans la molécule d'eau solide est de 178 picomètres.
En résumé, la longueur de la liaison hydrogène HF dans le fluorure d'hydrogène cristallin est de 157 picomètres, tandis que dans la molécule d'eau solide, elle est de 178 picomètres. Le calcul du moment dipolaire et l'utilisation de formules spécifiques permettent de déterminer ces valeurs.
Physique-Chimie
Chimie
MPSI/PCSI

Halogènes
Dans cette vidéo, nous étudions les propriétés physiques des halogènes. Nous cherchons à corréler l'évolution des températures de changement d'état des dihalogènes aux rayons de Van der Waals des atomes correspondants. Les températures de fusion et d'ébullition dépendent des interactions entre les molécules. Dans le cas des halogènes, les interactions de type Van der Waals sont à l'œuvre, en particulier les interactions de type London. Ces interactions dépendent de la taille du nuage électronique. Plus le nuage électronique est gros, plus les interactions de London sont fortes et plus les températures de fusion et d'ébullition sont élevées.
Dans un autre exercice, nous étudions l'évolution des températures de fusion pour des espèces de formule Cx4. Les interactions en jeu sont toujours de type London. Lorsque le volume de polarisabilité des liaisons Cx augmente, les températures de fusion augmentent également.
Enfin, nous analysons l'évolution des températures de fusion pour des espèces chlorées. Les interactions entre molécules sont de type qui somme, dipôle permanent. En gardant des interactions de type London, la température de fusion augmente lorsque le volume de polarisabilité et la norme du moment dipolaire augmentent.
Cet exercice permet de comprendre et d'analyser les interactions moléculaires en fonction des observations expérimentales.
Physique-Chimie
Chimie
MPSI/PCSI
Moment dipolaire
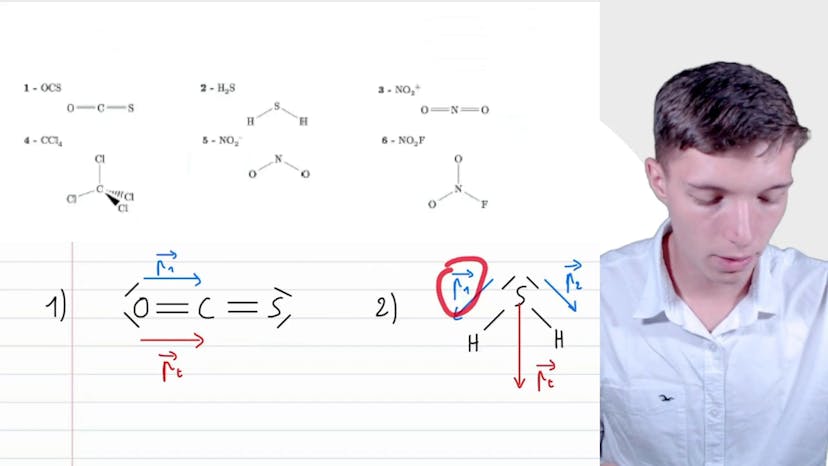
Dans cette vidéo, Matisse de Studio aborde le sujet de la représentation des moments dipolaires des molécules chimiques. Il explique comment déterminer la direction et le sens de ces moments pour différents édifices chimiques. Les molécules étudiées sont OCS, H2S, N2O+, CCL4, et NO2-. Matisse commence par expliquer comment la différence d'électronégativité entre les atomes impliqués influence la polarité de la liaison chimique. Pour OCS, il y a une différence d'électronégativité entre l'oxygène et le carbone, mais pas entre le soufre et le carbone. Par conséquent, il y a un seul moment dipolaire entre l'oxygène et le carbone. Pour H2S, la différence d'électronégativité entre l'hydrogène et le soufre est faible, mais il existe deux moments dipolaires en raison des différentes liaisons. Pour N2O+, il y a une différence suffisante d'électronégativité pour qu'il y ait un moment dipolaire, mais étant donné que la molécule est symétrique, les deux moments dipolaires se compensent et le moment dipolaire total est nul. Pour CCL4, qui a une forme de tétraèdre, les quatre moments dipolaires se compensent également, donnant un moment dipolaire total nul. Pour NO2-, une différence de longueur entre les liaisons simple et double impliquant l'azote et l'oxygène indique une différence de moment dipolaire, mais en raison de la mesomérie, les liaisons sont équivalentes et le moment dipolaire global est orienté verticalement. Enfin, pour NO2-, où deux atomes d'oxygène sont reliés de manière équivalente par mesomérie, le moment dipolaire global est faible mais légèrement orienté. Matisse souligne que la détermination des moments dipolaires est importante pour comprendre les propriétés physico-chimiques des molécules.
Physique-Chimie
Chimie
MPSI/PCSI
Interactions aquatiques
Dans cette vidéo, Matisse de Studio aborde les différences de propriétés en relation avec l'eau. Il commence par interpréter la solubilité à température ambiante de trois composés gazeux : le CO2, le SO2 et le NH3. Le CO2 a une solubilité assez faible car il est apolaire, contrairement à l'eau qui est polaire et protique. Le SO2, en revanche, a une solubilité plus importante car il établit des liaisons de quissomme avec l'eau. L'ammoniaque est très soluble dans l'eau car elle est polaire, protique et peut former des liaisons de quissomme ainsi que des liaisons hydrogènes avec l'eau.
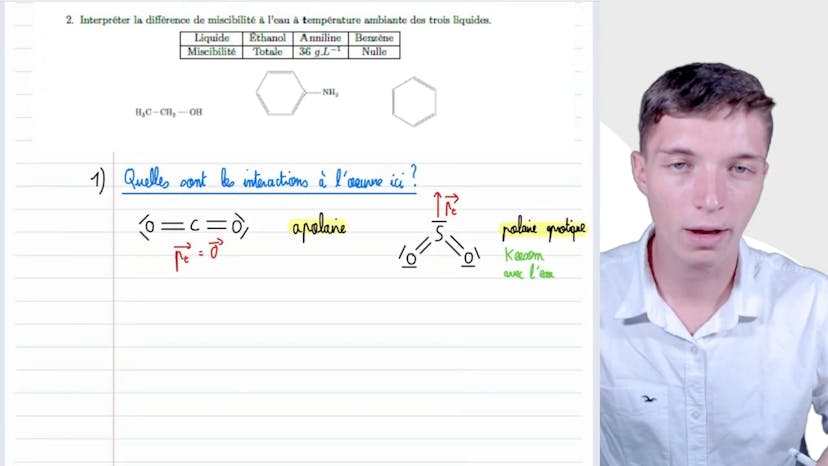
Ensuite, Matisse analyse la différence de solubilité dans l'eau à température ambiante de trois liquides : l'éthanol, l'aniline et le benzène. L'éthanol est polaire et protique, ce qui explique sa grande miscibilité avec l'eau. L'aniline est faiblement polaire et protique, ce qui lui confère une faible interaction avec l'eau. Le benzène, en revanche, est apolaire et aprotique, d'où son absence totale de solubilité dans l'eau.
Il souligne l'importance de ces notions en chimie expérimentale lors de l'isolation ou de l'extraction de certains éléments actifs ou molécules. Il mentionne également que le cyclohexane est un solvant très particulier et intéressant à cet égard en raison de son caractère apolaire et aprotique.
En conclusion, Matisse rappelle l'importance de comprendre quelles interactions peuvent se produire entre les différents solvants et souligne que "qui se ressemble s'assemble".
Physique-Chimie
Chimie
MPSI/PCSI
Isomères de position
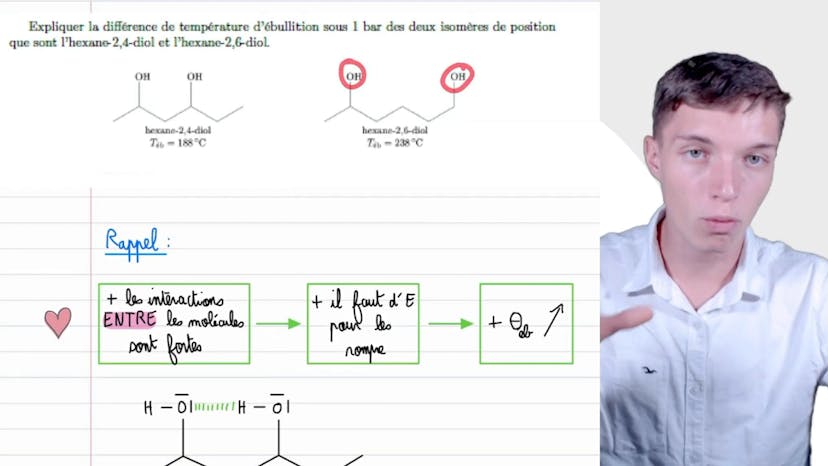
Dans cette vidéo, nous analysons la différence de température d'ébullition entre deux isomères de position, l'exam 2,4-diol et l'exam 2,6-diol. Les températures d'ébullition dépendent des interactions entre les molécules. Plus ces interactions sont fortes, plus il faut d'énergie pour les rompre, ce qui entraîne une température d'ébullition plus élevée.
Les deux isomères diffèrent par la position de leurs groupements hydroxyle. Dans le premier isomère, les groupements hydroxyle sont rapprochés, formant une liaison hydrogène intramoléculaire qui renforce la cohésion de la molécule. Cependant, cela diminue les interactions entre les molécules.
Dans le deuxième isomère, il y a deux groupements hydroxyle, permettant des liaisons hydrogène avec d'autres molécules. Ainsi, la cohésion entre les molécules du solvant est renforcée et doit être rompue lors de l'ébullition. Ce raisonnement explique pourquoi l'isomère exam 2,6-diol a une température d'ébullition plus élevée que l'isomère exam 2,4-diol.
Il est important de comprendre ces différences entre les liaisons intramoléculaires et intermoléculaires pour appréhender les propriétés physiques des molécules. Cette analyse nous permet de comprendre pourquoi les isomères peuvent présenter des différences de température d'ébullition.
Physique-Chimie
Chimie
MPSI/PCSI

Composés hydrogénés
Dans cette vidéo, nous examinons l'évolution des températures d'ébullition des composés hydrogénés des éléments des colonnes 14 et 17 de la classification périodique. Le tableau 6 présente ces températures d'ébullition sous une pression atmosphérique standard. En utilisant la représentation graphique de la molécule de méthane, nous pouvons déduire que cette molécule est apolaire. Les autres composés hydrogénés de la colonne ont également une géométrie tétraédrique et sont apolaires. La raison pour laquelle les composés hydrogénés des éléments de la colonne 14 ont des températures d'ébullition plus basses que ceux de la colonne 17 est due aux interactions moléculaires. Les composés hydrogénés des éléments de la colonne 17 sont polaires et ont des interactions de type quissomme, ce qui rend leur température d'ébullition plus élevée. Les interactions de London prédominent dans les molécules de taille plus importante, comme HBr et HI, ce qui explique l'augmentation continue des températures d'ébullition. Une anomalie est observée pour HF, où la température d'ébullition est plus élevée que prévu. Cela est dû à la nature très électronégative de l'atome de fluor, qui entraîne des liaisons hydrogènes plus fortes entre les molécules de HF. Ainsi, il faut plus d'énergie pour séparer ces molécules, ce qui conduit à une température d'ébullition élevée. Cette transcription fournissait une analyse des interactions moléculaires et de leurs effets sur les températures d'ébullition des composés hydrogénés.
Physique-Chimie
Chimie
MPSI/PCSI

Energie d'activation
Dans cette vidéo, Matisse de Studio explique comment calculer l'énergie d'activation d'une réaction chimique en utilisant la formule d'Arenus. Il commence par expliquer que la vitesse de réaction double lorsque la température passe de 300 Kelvin à 400 Kelvin. Il fait l'hypothèse que la constante de vitesse double également. En utilisant la loi d'Arenus, il montre que la constante de vitesse est égale à A multiplié par l'exponentielle de moins EA/RT, où EA représente l'énergie d'activation, A est un facteur pré-exponentiel, R est la constante des gaz parfaits et T est la température de réaction. Sachant que la constante de vitesse double, il nomme K1 et K2 les constantes de vitesse pour les réactions réalisées à 300 Kelvin et 400 Kelvin respectivement. En utilisant la loi d'Arenus, il établit l'équation K2 = 2K1. En simplifiant l'équation, il isole l'énergie d'activation EA et trouve que EA est égal à R ln 2 divisé par 1/T1 - 1/T2. Il conclut que l'énergie d'activation de la réaction est de 6,9 kJ/mol. Il conseille de prendre son temps pour comprendre l'énoncé, donner des noms aux variables et utiliser la formule d'Arenus pour résoudre l'exercice.
Physique-Chimie
Chimie
MPSI/PCSI
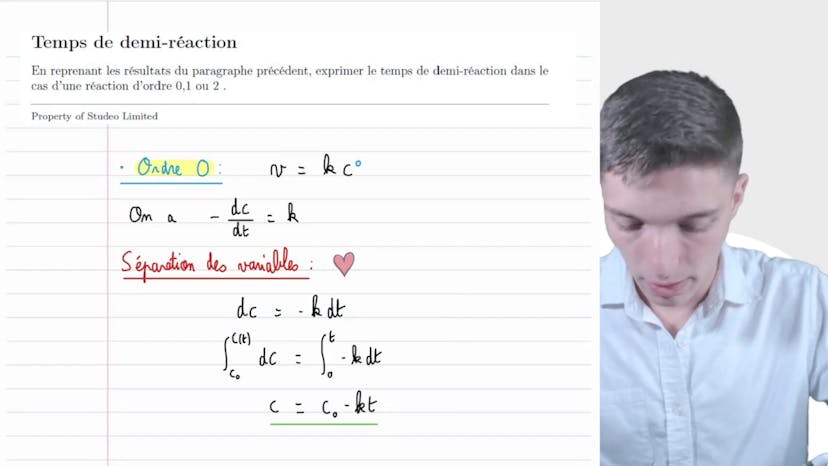
Temps de demi réaction
Dans cette vidéo, Mathis de Studio traite des différents temps de demi-réaction pour les réactions d'ordre 0, 1 et 2. Il explique que ces notions sont essentielles à connaître pour les examens et les exercices.
Pour les réactions d'ordre 0, la vitesse de réaction peut être exprimée comme V = k * [A]^0, où [A]^0 représente la concentration d'une espèce qui disparaît. En résolvant cette équation, on obtient que la concentration en fonction du temps est donnée par c = c0 - kt, où c0 est la concentration initiale et k est la constante de vitesse. Le temps de demi-réaction peut alors être calculé en résolvant c = c0/2, ce qui donne t1/2 = c0/(2k).
Pour les réactions d'ordre 1, la vitesse de réaction peut être exprimée comme V = k * [A]^1, où [A]^1 représente la concentration d'une espèce qui disparaît avec un coefficient stoichiométrique de 1. En suivant les étapes similaires, on obtient que la concentration en fonction du temps est donnée par c = c0 * e^(-kt). Le temps de demi-réaction peut alors être calculé en résolvant c = c0/2, ce qui donne t1/2 = ln(2)/k.
Enfin, pour les réactions d'ordre 2, la vitesse de réaction peut être exprimée comme V = k * [A]^2, où [A]^2 représente la concentration d'une espèce qui disparaît avec un coefficient stoichiométrique de 2. En suivant les étapes similaires, on obtient que la concentration en fonction du temps est donnée par c = c0/(1 + c0kt). Le temps de demi-réaction peut alors être calculé en résolvant c = c0/2, ce qui donne t1/2 = 1/(c0k).
En résumé, cette vidéo explique comment déterminer les temps de demi-réaction pour les réactions d'ordre 0, 1 et 2, en utilisant les équations d'évolution de la concentration en fonction du temps.
Physique-Chimie
Chimie
MPSI/PCSI
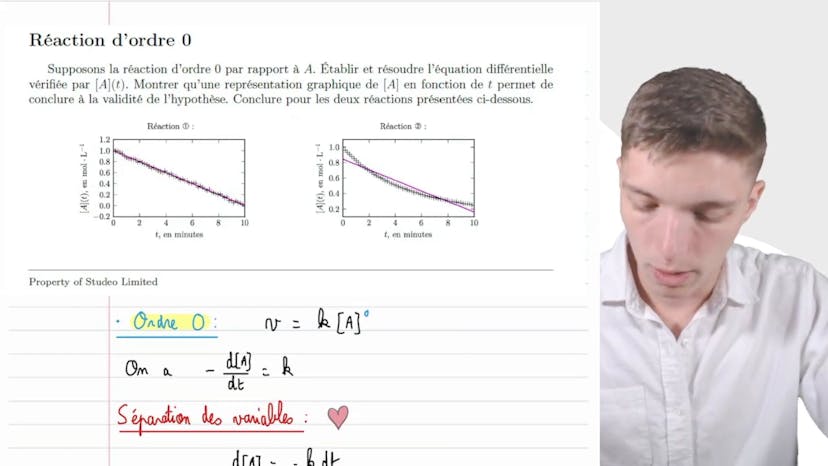
Réaction d'odre 0
Dans cette vidéo, nous vérifions si une réaction chimique est d'ordre zéro ou non. Pour cela, nous faisons une hypothèse sur l'ordre de réaction et examinons les conséquences de cette hypothèse sur la cinétique de la réaction. Nous devons établir et résoudre l'équation différentielle qui décrit la concentration du réactif en fonction du temps. En analysant la représentation graphique de la concentration en fonction du temps, nous pouvons conclure si notre hypothèse est valide ou non. Dans cet exercice, nous obtenons deux courbes différentes pour les deux réactions étudiées. La première courbe est une droite qui passe par tous les points, indiquant une cinétique d'ordre zéro, tandis que la deuxième courbe est une courbe polynomial ou convexe, indiquant une cinétique différente de l'ordre zéro. En résolvant l'équation différentielle, nous obtenons une fonction affine décroissante pour la première réaction, confirmant notre hypothèse. En conclusion, la première réaction est d'ordre zéro par rapport au réactif A, tandis que la deuxième réaction n'est pas d'ordre zéro. Cette analyse nous permet de déterminer l'ordre de réaction à partir de la courbe d'évolution de la concentration. C'est un exemple puissant de la puissance des calculs analytiques et des observations expérimentales en cinétique chimique.


