Cours d'apprentissage en ligne

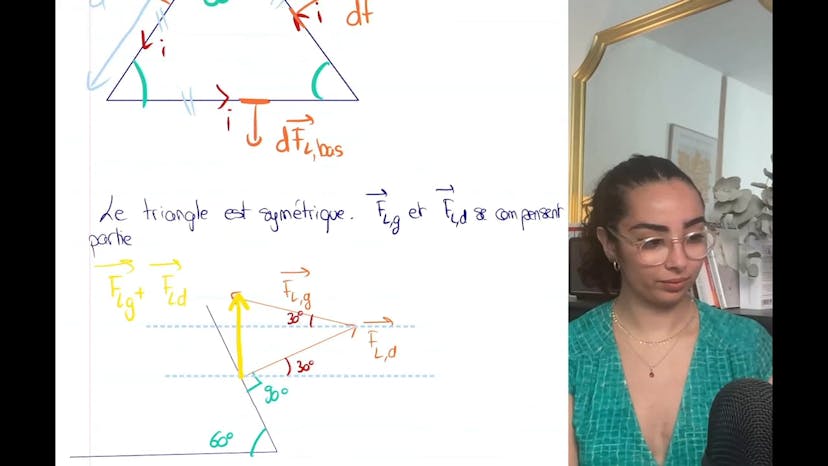
Circuit triangulaire

Aujourd'hui, nous allons étudier la force qui agit sur un circuit triangulaire, soumis à un champ magnétique. L'exercice consiste à calculer cette force. Il y a deux manières de le faire : soit en utilisant des projections et des calculs trigonométriques, soit en cherchant des forces qui s'annulent mutuellement. Dans ce cas, nous pouvons voir que la force sur le côté inférieur du triangle est facile à calculer, tandis que les forces sur les côtés gauche et droit se compensent mutuellement. En utilisant la relation de Chasles, nous pouvons conclure que la force résultante est uniquement vers le haut. Pour un triangle équilatéral, les forces sur les côtés gauche et droit sont identiques et inclinées à un angle de 30 degrés. Ainsi, la force résultante vers le haut est égale à la norme de la force de la place multipliée par racine de 3 moins 1. Pour un triangle isocèle, où un angle est de 30 degrés, nous utilisons la même méthode et trouvons que la force résultante est égale à 2A sin(alpha/2) multipliée par la norme de la force de la place, moins la norme de la force qui va vers le bas. Il est important de vérifier si les résultats obtenus pour différentes géométries correspondent ; dans ce cas, nous constatons que la formule pour le triangle équilatéral peut être dérivée de celle du triangle isocèle. Cela conclut la vidéo et nous continuerons notre étude sur l'induction dans la prochaine leçon.

Maths Spé

Terminale

Inégalité de Bernoulli : Démo

Dans cette vidéo, nous allons démontrer ensemble l'immédiateté de Bernoulli en utilisant la méthode de démonstration par récurrence. Pour repérer qu'une démonstration par récurrence est attendue, il faut être attentif aux mots-clés tels que "pour tout entier naturel N". Une démonstration par récurrence permet d'avoir un chemin à suivre lorsqu'on ne sait pas comment commencer une démonstration en mathématiques. Lorsqu'une formule est donnée, cela indique qu'une récurrence est possible. Pour éviter de perdre des points, il est recommandé d'écrire immédiatement les trois parties de la démonstration par récurrence: (1) initialisation, (2) hérédité, (3) conclusion. Ce rappel permet d'éviter d'oublier une partie et de perdre des points par manque de clarté. Il est important de ne pas simplement donner le résultat, mais de le justifier. Par exemple, pour l'initialisation, il faut expliquer que 1^0 = 1 et que 1+0*a = 1, donc l'assertion est vérifiée. Ensuite, il est conseillé de rédiger la partie de l'hérédité en écrivant le point de départ et le point d'arrivée de la démonstration. Cela permet de garder le cap et de ne pas se perdre dans la rédaction. Ensuite, en multipliant les deux membres de l'hypothèse de récurrence par (1+a), on obtient l'expression à démontrer. En développant, on peut observer que certains termes se simplifient et on peut montrer que l'expression est plus grande ou égale à celle du point d'arrivée. En conclusion, on peut écrire la phrase type de la démonstration par récurrence en affirmant que l'assertion est vérifiée pour tout entier naturel n. Il est important de noter que la structure de la démonstration et la clarté de la rédaction sont primordiales pour éviter de perdre des points.

Equivalents usuels

Dans cette vidéo, Corentin nous présente un exercice qui nous permet de comprendre le concept de suites équivalentes. Il commence par rappeler la définition des suites équivalentes : UN et VN sont équivalentes lorsque le quotient UN/VN tend vers 1 lorsque UN tend vers l'infini. Ensuite, il nous rappelle comment calculer la limite d'une fraction rationnelle en factorisant par le terme le plus fort. Il résout ensuite différentes questions : - Dans la question 1, il détermine si N est équivalent à N+1 lorsque N tend vers l'infini. En factorisant par N, il conclut que la limite de cette expression est égale à 1, donc N est bien équivalent à N+1 en plus l'infini. - Dans la question 2, il détermine si N^2+1 est équivalent à N^2 en plus l'infini. En factorisant par N^2, il conclut que la limite de cette expression est égale à 1, donc N^2+1 est bien équivalent à N^2 en plus l'infini. - Dans la question 3, il détermine si Ln(N) est équivalent à Ln(10^6N). En utilisant la propriété Ln(AB) = Ln(A) + Ln(B), il factorise par Ln(N) et conclut que la limite de cette expression est égale à 1, donc Ln(N) est bien équivalent à Ln(10^6N) en plus l'infini. - Dans la question 4, il détermine si Ln(N) est équivalent à Ln(N+10^6). En utilisant la propriété Ln(A+B) = Ln(A) + Ln(B), il conclut que la limite de cette expression ne tend pas vers 1, donc Ln(N) n'est pas équivalent à Ln(N+10^6). - Dans la question 5, il détermine si exp(N) est équivalent à exp(2N). En utilisant les propriétés des exponentielles, il conclut que la limite de leur quotient ne tend pas vers 1, donc exp(N) n'est pas équivalent à exp(2N). - Dans la question 6, il détermine si Ln(N) est équivalent à Ln(N+1). En décomposant Ln(N+1) en Ln(N) + Ln(1) + 1/N, il factorise par Ln(N) et conclut que la limite de cette expression est égale à 1, donc Ln(N) est bien équivalent à Ln(N+1). Corentin nous rappelle l'importance de ces concepts et nous encourage à bien les comprendre pour réussir nos exercices.

Equivalents niveau 2

Dans ce cours, l'exercice consiste à trouver les équivalents de différentes expressions. Pour cela, on utilise des méthodes de calcul et des propriétés mathématiques. La première question demande de trouver un équivalent de l'expression "Un" qui est égal à 1/(n-1) - 1/n + 1. Pour trouver cet équivalent, on passe au même dénominateur et on remarque que n^2 - 1 est équivalent à n^2. Donc Un est équivalent à 2/n^2. La deuxième question demande de déterminer un équivalent de l'expression "Vn" qui est égale à racine de n + 1 - racine de n - 1. On utilise le développement limité de racine de 1 + x et racine de 1 - x pour trouver que racine de n + 1 est équivalente à racine de n + 1/2*1/√n + petit o(1/√n). En simplifiant, on obtient que Vn est équivalent à 1/√n. La troisième question concerne l'expression "Wn" qui est complexe. On factorise cette expression et en simplifiant, on obtient que Wn est équivalente à -n/2. La dernière question demande de trouver un équivalent de l'expression "Zn" qui est égale à sin(2/√(n+1))/√(n+1) + 1/√(n+1). En utilisant le développement limité de sin(2x), on trouve que Zn est équivalente à 1/√(n+1). On utilise ensuite le résultat précédent pour dire que Zn est équivalente à 1/√n. En résumé, on a trouvé les équivalents suivants : - Un est équivalent à 2/n^2 - Vn est équivalent à 1/√n - Wn est équivalent à -n/2 - Zn est équivalent à 1/√n

Equivalents et signe

Ce cours porte sur la comparaison d'équivalences de fonctions exponentielles. On considère deux fonctions f et g définies au voisinage d'un réel A. On veut montrer que exponentielle de f est équivalent à exponentielle de g si et seulement si la limite en A de f-g est égale à zéro. Pour démontrer cette équivalence, on raisonne par équivalence et on utilise la définition de l'équivalent. On sait que exponentielle de f est équivalent à exponentielle de g en A, ce qui signifie que exponentielle de f divisé par exponentielle de g tend vers 1 en A. En passant par le logarithme naturel des deux côtés et en utilisant la continuité du logarithme, on obtient que f-g tend vers 0 en A. Ensuite, on se demande si le fait que f soit équivalent à g en A implique forcément que exponentielle de f est équivalent à exponentielle de g en A. La réponse est non. On trouve un contre-exemple en prenant f(x)=x et g(x)=x+1. On a f équivalent à g car x+1 est équivalent à x, mais exponentielle de f(x) n'est pas équivalent à exponentielle de g(x) car leur quotient n'est pas égal à 1. En conclusion, on constate qu'on ne peut pas composer librement les équivalents et il faut être prudent dans les compositions de fonctions. Dans certains cas particuliers, cela peut être possible, mais en général, il faut faire attention.

Avec des factorielles

Ce cours montre que la somme de factoriel k pour k allant de 0 à n est équivalente à factoriel n. Pour prouver cela, on décompose la somme et on montre que chaque terme tend vers 0 lorsque n tend vers l'infini. En utilisant des techniques de majoration, on conclut que la somme totale tend vers 1, ce qui démontre l'équivalence recherchée.

Equivalence de sommes partielles

Dans ce cours, nous étudions les équivalents de séries réelles positives. Nous cherchons à montrer que si la série Un est équivalente à Vn et si la limite de Vn tend vers l'infini, alors nous pouvons sommer ces équivalents. Ensuite, nous appliquons ces résultats à deux exemples : trouver un équivalent de la série 1/√k et de la série ln(k). Nous montrons que la première série est équivalente à 2√n et que la deuxième série est équivalente à nln(n).

Lemme de Césaro

Dans ce cours, on étudie une suite U définie par U0 et Un+1 = sin(Un). Dans la première partie, on montre que cette suite est strictement positive, décroissante et tend vers zéro. On utilise le fait que le sinus est croissant sur l'intervalle [0, π/2] et que sin(0) = 0. Ensuite, on admet que si une suite U a pour limite zéro, alors sin(Un) = Un - Un^3/6 + petit o (Un^3). On cherche alors à déterminer un réel alpha tel que la suite Vn = Un+1^alpha - Un^alpha ait une limite réelle non nulle. En utilisant le développement limité de sin(Un), on trouve que Vn est équivalent à 1/3 + petit o (1). En appliquant le lemme de Césaro à la suite Vn, on obtient un équivalent simple de Un lorsque n tend vers l'infini. On utilise une somme télescopique et on trouve que 1/Un^2 est équivalent à 3/n. En conclusion, on peut dire que la suite U est équivalente à la racine carrée de 3/n lorsque n tend vers l'infini.

Fonctions - Métropole 2022

Dans cet exercice, nous étudions différentes questions sur les fonctions logarithmes. La première question concerne l'équation f(2x) = log(1 + x^2) = 2022. En passant à l'exponentielle des deux côtés de l'équation, nous obtenons 1 + x^2 = e^2022. Comme e^2022 est strictement positif, l'équation admet deux solutions : la racine carrée de e^2022 et son opposé. La deuxième question porte sur la convexité de la fonction G définie par G(x) = x log(x) - x^2. En calculant la dérivée seconde de G, nous pouvons observer que celle-ci est positive entre 0 et 1/2, puis devient négative à partir de 1/2. Par conséquent, la fonction G a un unique point d'inflexion. La troisième question demande de trouver une primitive de la fonction f définie par f(x) = x / (1 - x^2). En identifiant u' / u, nous pouvons reconnaître la dérivée de log(1 - x^2). Ainsi, la primitive de f est -1.5 log(1 - x^2). La quatrième question concerne l'ensemble de définition de la fonction associée à l'expression log(-x^2 - x + 6). Comme nous savons que le logarithme est défini lorsque son argument est strictement positif, nous devons étudier le signe du polynôme -x^2 - x + 6. En déterminant son discriminant, nous trouvons deux racines, et en analysant les signes entre et à l'extérieur de ces racines, nous concluons que l'ensemble de définition est (-3, 2). Enfin, la dernière question concerne une inéquation logarithmique. En simplifiant l'expression, nous obtenons x + 3 < (x + 1)^2. Après étude d'un polynôme du second degré, nous déterminons que l'inégalité est vérifiée pour x appartenant à (-∞, -2) U (1, +∞).

Probabilités - Métropole 2022

Dans cet exercice de bac sur les probabilités, nous devons calculer des probabilités en utilisant des intersections et des arbres de probabilités. Nous devons également utiliser des probabilités conditionnelles et parler d'indépendance. Dans la deuxième partie de l'exercice, nous devons travailler avec des variables aléatoires qui suivent une loi normale. Dans la première partie, nous avons un coyote qui peut être malade (M) ou non malade (non M). Un test est réalisé et peut être positif (T) ou négatif (non T). On nous donne les informations suivantes : si le coyote est malade, le test est positif dans 97% des cas, et s'il n'est pas malade, le test est négatif dans 95% des cas. Nous devons d'abord calculer la probabilité que le coyote soit malade et que son test soit positif. Cette probabilité est donnée par l'intersection entre M et T, soit 0,7 * 0,97 = 0,679. Ensuite, nous devons démontrer que la probabilité de T est égale à 0,694. Nous utilisons la formule des probabilités totales en utilisant les probabilités conditionnelles. Après calcul, nous trouvons bien 0,694. Nous devons également calculer la valeur prédictive positive du test, c'est-à-dire la probabilité que le coyote soit malade sachant que son test est positif. En utilisant la formule des probabilités conditionnelles, nous trouvons une valeur de 0,978. Par analogie avec la question précédente, nous devons défin

Géométrie - Métropole 2022

Dans cet exercice de géométrie dans l'espace, nous sommes confrontés à différents problèmes liés à la géométrie et à la trigonométrie. Les principales étapes de l'exercice sont les suivantes : 1. Trouver les coordonnées des points E, F, G et K dans le repère donné. 2. Montrer que le vecteur N est orthogonal au plan E, G, K en effectuant des calculs de produit scalaire. 3. Trouver l'équation cartésienne du plan E, G, K en utilisant le vecteur normal et un point du plan. 4. Déterminer une représentation paramétrique de la droite D orthogonale au plan E, G, K et passant par F. 5. Calculer les coordonnées du projeté orthogonal de F sur le plan E, G, K en résolvant un système d'équations. 6. Justifier que la longueur LF est égale à 2/3 en utilisant la formule de calcul de distance dans l'espace. 7. Calculer l'aire du triangle EFG et en déduire le volume du tétraèdre EFGK en utilisant les formules appropriées. 8. Déterminer le volume du tétraèdre FPMN en utilisant le théorème de la droite des milieux. En résumé, cet exercice aborde différents concepts de géométrie et de trigonométrie dans l'espace, tels que l'orthogonalité, les équations cartésiennes, les représentations paramétriques, les projetés orthogonaux, les longueurs, les aires et les volumes dans le contexte d'un tétraèdre.