Cours d'apprentissage en ligne

Type Mines : Partie A - 3/4

Dans ce cours, Corentin parle de la Lipschitzianité et de l'uniformité de continuité des fonctions. Il commence par montrer que si une fonction est Lipschitzienne et qu'un réel alpha est ajouté à son argument, alors la nouvelle fonction obtenue est aussi Lipschitzienne. Ensuite, il montre que la fonction sinus est Lipschitzienne et que sa fonction dérivée, le cosinus, est également Lipschitzienne. Finalement, il explique ce qu'est une application uniformément continue et montre que si une fonction est Lipschitzienne, alors elle est également uniformément continue. Il prouve ensuite que la réciproque, à savoir qu'une fonction uniformément continue n'est pas forcément Lipschitzienne, est fausse. Il illustre cela par un exemple de fonction uniformément continue mais non Lipschitzienne, la fonction valeur absolue de x à la racine.

Type Mines : Partie B - 4/4

Dans cette vidéo, Corentin traite de la recherche de solutions Lipschitzienne d'une équation donnée. Il commence par montrer qu'une équation vérifiée pour tout réel X et tout entier naturel N peut être résolue par récurrence sur N. Ensuite il démontre que cette équation ne permet au plus qu'une solution dans l'ensemble des fonctions Lipschitzienne lorsque la valeur absolue de lambda est strictement inférieure à 1. Lorsque f est une fonction constante de valeur 1, la solution Lipschitzienne unique est trouvée en résolvant l'équation et en montrant qu'elle est constante. Enfin, Corentin démontre que la fonction donnée par une formule particulière est la solution unique Lipschitzienne de l'équation lorsque f est égale à cosinus et sinus de x.

Fonctions hyperboliques

Dans cette vidéo, Corentin nous présente un exercice qui consiste à comprendre en profondeur toutes les fonctions trigonométriques. Il commence par nous donner quelques rappels sur le sinus hyperbolique et l'arc tangente, puis présente les questions de l'exercice. Il montre ensuite comment résoudre chaque question, en détaillant les étapes et en utilisant des formules et des propriétés de fonctions trigonométriques. Finalement, il conclut en montrant que x est égal au logarithme de la tangente de T sur 2 plus pi sur 4.

Fonctions hyperboliques inverses

Dans cette vidéo, Corentin nous propose un exercice pour maîtriser les calculs trigonométriques. Il s'agit de simplifier six formules trigo. Il commence par rappeler que le cosinus hyperbolique au carré plus le sinus hyperbolique au carré est égal à 1. En utilisant cette formule, il simplifie le cosinus hyperbolique de l'arc sinus hyperbolique. Ensuite, il utilise la définition de la tangente hyperbolique pour simplifier la tangente hyperbolique de l'arc sinus hyperbolique. Pour simplifier le sinus hyperbolique de 2 arc sinus hyperbolique, il utilise une formule de somme. Pour la question deux, il utilise les formules des arcs cosinus hyperboliques, arcs sinus hyperboliques et arcs tangents hyperboliques pour simplifier le sinus hyperbolique de l'arc cosinus hyperbolique. Au dénominateur, il utilise la forme conjuguée pour simplifier le résultat. Enfin, il utilise la formule de somme pour simplifier le cosine hyperbolique de 3 arc cosine hyperbolique de x. En résumé, Corentin donne des astuces et des conseils pour simplifier les formules trigo de manière efficace.

Fonctions arctan et arcsin

Dans cette vidéo, Corentin explique comment simplifier une expression mathématique complexe en utilisant des techniques de calcul et en trouvant le domaine de définition de la fonction. Il commence par déterminer le domaine de définition de la fonction en utilisant les propriétés de la fonction arc tangente et arc sinus. Ensuite, il détermine le domaine de définition de la dérivée de la fonction en utilisant les propriétés de la fonction racine carrée et arc sinus. Enfin, il simplifie l'expression de la fonction en calculant sa dérivée et en déterminant sa constance sur tout le domaine de définition. Le résultat final est que la fonction est constante sur 0,1 avec une valeur de pi / 2.

Fonctions hyperboliques

Dans cette vidéo, Corentin nous explique un exercice de mathématiques sur les fonctions trigonométriques. Il commence par poser T égal à arc tangente de SH de x, et montre ensuite quelques relations importantes comme tangente de T égale à sinus hyperbolique de x et sinus de T égale à tangente hyperbolique de x. Il explique également les limites et le graphe de la fonction sinus hyperbolique et de l'arc tangente. Il montre comment prouver que 1 sur cosinus de T est égal à cosinus hyperbolique de x et que x est égal au logarithme de la tangente de T sur 2 plus pi sur 4. En utilisant des démonstrations rigoureuses, Corentin nous permet de mieux comprendre les fonctions trigonométriques.

Fonctions hyperboliques inverses

Dans cette vidéo, Corentin nous présente un exercice de simplification de six formules trigonométriques en utilisant les fonctions hyperboliques. Il commence par rappeler que cosinus hyperbolique au carré plus sinus hyperbolique au carré est égal à 1, généralisé au cosinus hyperbolique. Ensuite, il simplifie les formules en utilisant différentes définitions et formules, telles que la définition de la tangente hyperbolique et la somme des sinus hyperboliques. Finalement, il nous montre comment simplifier une formule avec des racines carrées en passant à la forme conjuguée. Corentin nous encourage à bien connaître les fonctions réciproques de l'arc cosinus hyperbolique, de l'arc sinus hyperbolique et de l'arc tangente hyperbolique pour simplifier les formules. Il conclut avec la formule simplifiée de sine hyperbolique de arg cosine hyperbolique, tangente hyperbolique de arg cosine hyperbolique et cosine hyperbolique de 3 arg cosine hyperbolique. Keywords: trigonométrie, fonctions hyperboliques, simplification, arcsinus hyperbolique, arccosinus hyperbolique, arctangente hyperbolique, formules trigonométriques, cosinus hyperbolique, sinus hyperbolique, racines carrées, forme conjuguée

Fonctions hyperboliques inverses (2)

Dans cette vidéo, Corentin résout un exercice de mathématiques qui mélange théorème d'analyse générale et trigonométrie. Il montre que l'équation arg s h de x plus arg c h de x est égale à 1 a une unique solution, qu'il détermine ensuite en se servant du théorème de l'abjection et en passant au s h des deux côtés de l'équation. En utilisant des formules de trigonométrie, il simplifie l'équation et obtient que alpha est égal à 1 plus s h de 1 au carré divisé par 2 s h de 1.

Déterminer un PGCD

Dans cet exercice, on apprend à calculer le PGCD de deux nombres: 18 840 et 9828. La méthode la plus simple est l'algorithme d'Euclide, qui utilise des divisions euclidiennes successives. On commence par diviser le plus grand nombre par le plus petit. Ensuite, on continue à diviser le diviseur par le reste jusqu'à obtenir un reste de 0. Le PGCD est alors le dernier reste non nul. Dans ce cas, le PGCD de 18 840 et 9828 est 12.

Différence et quotient

Dans cet exercice, on doit trouver deux nombres entiers dont la différence est égale à 538. On sait également que lorsqu'on divise l'un par l'autre, le quotient est 13 et le reste est 34. On note ces deux nombres A et B, et on suppose que A est plus grand que B. On écrit deux équations pour ces informations et on résout le système : A-B=538 et A=13B+34. On trouve B=42, ce qui nous permet ensuite de trouver A=580.

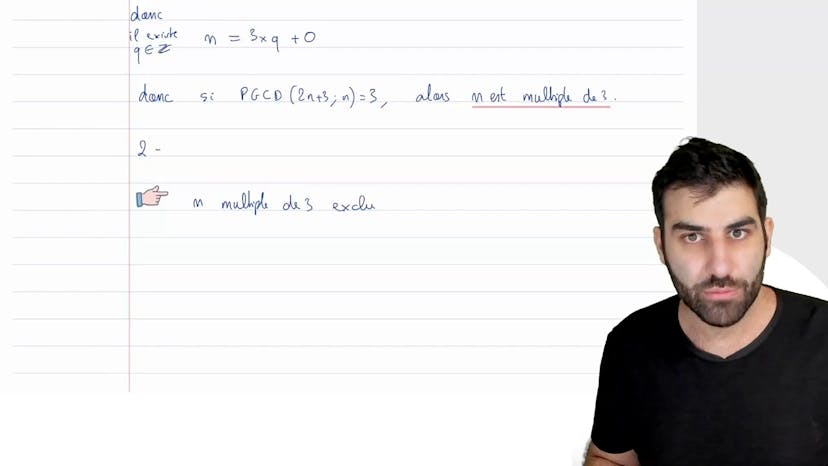
PGCD qui dépend de n

Dans cet exercice, on cherche à déterminer l'ensemble des entiers naturels n permettant que le PGCD de 2n+3 et de n soit égal à 3. En effectuant la division euclidienne de 2n+3 par n, on trouve que si le PGCD est égal à 3, alors n est divisible par 3. Ensuite, si l'on cherche à déduire l'ensemble des entiers n pour lesquels le PGCD de 2n+3 et de n est égal à 1, on remarque que lorsque n est multiple de 3, le PGCD ne peut pas être égal à 1. Ainsi, si n est de la forme 3k+2 ou 3k+1, où k est un entier naturel, alors le PGCD est égal à 1.