Cours d'apprentissage en ligne

Forme indéterminée 1 : factoriser par terme de plus haut degré

Dans cette leçon, nous étudions les différentes formes indéterminées pour le calcul de limites et comment les résoudre. Nous commençons par l'exemple d'un polynôme en n. La règle est que seul le terme de plus haut degré compte et prédomine. Pour démontrer cela rigoureusement, nous factorisons par le terme de plus haut degré. Dans cet exemple, le polynôme est n²-n. En factorisant par n², on obtient 1 + 1/n. Comme 1/n tend vers 0, on n'a plus de forme indéterminée et le résultat est donc l'infini. Cette règle s'applique à tous les polynômes, où le coefficient devant le terme de plus haut degré détermine le résultat. Dans ce cas, le coefficient est 1, donc le résultat est plus infini. Cela concerne les limites lorsque n tend vers plus infini.

Forme indéterminée 2 : la quantité conjuguée

Ce cours porte sur les méthodes de calcul pour les fonctions rationnelles, c'est-à-dire les polynômes divisés par d'autres polynômes. La technique utilisée est la même que pour les polynômes, on factorise par le terme de plus haut degré. Par exemple, si nous avons la suite Vn égale à 4n² sur n plus 1, nous identifions le terme de plus haut degré (2), et donc nous factorisons par n² en haut et par n en bas. Les n se simplifient et nous obtenons 4n au numérateur divisé par 1 plus 1 sur n qui tend vers 1. Ainsi, nous levons l'indétermination et constatons que par quotient, Vn tend vers plus infini. En outre, il existe trois cas possibles pour les fonctions rationnelles. Si le degré du polynôme au numérateur est strictement supérieur au degré du polynôme au dénominateur, celui-ci l'emporte et la limite tend vers plus infini. Si le degré du dénominateur est strictement supérieur au degré du numérateur, le dénominateur l'emporte et la limite tend vers 0. Si les degrés des polynômes au numérateur et au dénominateur sont égaux, la limite tend vers le rapport des coefficients dominants des deux polynômes. Par exemple, si nous prenons la suite Un égale à 3n² plus 2n plus 1 sur 4n² plus n plus 4, nous factorisons par le terme de plus haut degré (n²) en haut et en bas, ce qui nous donne 3 plus 2n plus 1 sur n² au numérateur, et 4 plus 1 sur n plus 4 sur n² au dénominateur. Finalement, la limite tend vers 3 quarts, le rapport des coefficients dominants. En conclusion, dès qu'il s'agit d'une fonction rationnelle, nous nous trouvons systématiquement dans l'un de ces trois cas.

Limite d'une somme géométrique

En terminale, lorsqu'on a une limite à calculer, il n'est pas nécessaire d'utiliser plusieurs méthodes. On doit d'abord vérifier si les termes de la somme correspondent à une suite arithmétique ou une suite géométrique. Si ce n'est pas le cas, cela nécessite une étude précise. Dans cet exemple, les termes de la somme sont les termes consécutifs d'une suite géométrique. On identifie donc la formule correspondante, qui est u0 * q^n, avec u0 = 1 et q = 3. Pour s'assurer de ne pas se tromper sur le nombre de termes, il est important de vérifier si l'expression est cohérente. Dans ce cas, on a vérifié que u0 = 1 et u1 = 3, ce qui est correct. En utilisant la formule générale, la somme s'exprime comme u0 * (1 - q^(n+1))/(1 - q). Il faut bien se rappeler que le nombre de termes est n+1, car il faut inclure le terme u0. On peut simplifier cette expression en utilisant les limites usuelles. On sait que q^n tend vers l'infini lorsque la valeur absolue de q est supérieure à 1. Par conséquent, la somme tend également vers l'infini. En conclusion, la somme de ces termes consécutifs de la suite géométrique tend vers l'infini.

Trouver à la calculette "le plus petit entier tel que..."

Dans ce cours, nous étudions une suite et cherchons à trouver le plus petit entier qui dépasse une certaine valeur. La suite est définie par u0 = 2 et la relation de récurrence un+1 = 3un. En observant cette relation, on peut voir que la suite augmente rapidement en multipliant chaque terme par 3. Ainsi, en partant d'une valeur positive, on se rend compte que la suite tend vers l'infini. En utilisant un petit programme, nous pouvons trouver le plus petit entier naturel tel que un > 1000. Le programme utilise une boucle while tant que un est inférieur à 1000. À chaque itération, un prend la valeur de 3un, et n est incrémenté de 1 pour compter le nombre d'opérations. À la fin, le programme affiche la valeur de n pour indiquer le rang de la suite. Il est également possible de trouver cette valeur par itération sans l'aide d'un programme. En multipliant successivement par 3, on peut voir que u3 = 54, u4 = 162, u5 = 486, et u6 = 1458. Ainsi, le premier entier tel que un > 1000 est 6. Il est important de bien comprendre le rôle de chaque élément du programme et les objectifs de l'exercice. Si des questions subsistent, il est possible de consulter la FAQ pour plus d'informations.

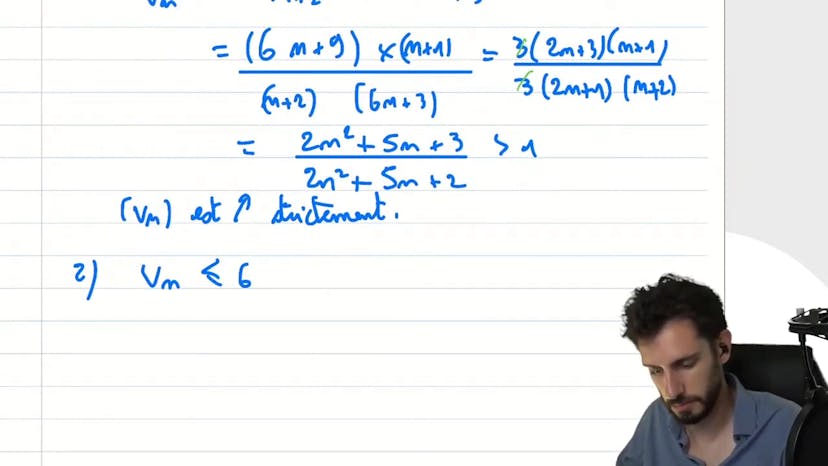
Suite-fraction

La première méthode consiste à étudier les variations de la suite vn = 6n + 3 / (n + 1). On utilise le critère de croissance en calculant le ratio vn+1 / vn et on trouve que ce ratio est strictement supérieur à 1. Donc la suite vn est strictement croissante. Ensuite, on montre que la suite est majorée par 6 en utilisant le fait que vn + tigre = 6 si et seulement si 6n + 3 + tigre = 6, ce qui est vrai lorsque tigre = 6 - 3. Donc vn + tigre = 6. Enfin, en utilisant le théorème de convergence monotone, on conclut que la suite vn converge. Dans la deuxième méthode, on écrit vn sous une autre forme en utilisant le fait que vn = 6n + 3 / (n + 1) = (6(n + 1) - 3) / (n + 1). On sépare la fraction en deux et on obtient une fonction f(n) = 6 - 3 / (n + 1), qui est une fonction hyperbole décroissante. Comme f est décroissante sur R+, on en déduit que la suite vn est croissante. De plus, on remarque que 6 - 3 / (n + 1) est égal à 6 pour tout n entier. Donc la suite vn est majorée par 6. Enfin, on utilise la limite classique de 3 / (n + 1) qui tend vers 0 lorsque n tend vers l'infini. Donc la limite de vn est 6. En résumé, la suite vn = 6n + 3 / (n + 1) est une suite croissante majorée par 6 et elle converge vers 6.

Plein de limites !

Ce cours traite de différentes méthodes de gestion des limites. Deux méthodes principales sont présentées : la méthode du terme dominant et la méthode de l'encadrement. La méthode du terme dominant consiste à comparer les termes dominants en haut et en bas d'une fraction pour déterminer le comportement de la suite. On peut factoriser en haut et en bas par le terme dominant, ce qui permet de conclure que la suite tend vers 0. La méthode de l'encadrement est utilisée dans le cas où la question concerne les limites d'une suite avec des puissances négatives et des fonctions trigonométriques. Il suffit d'encadrer ces termes entre -1 et 1 et d'appliquer un théorème d'encadrement pour obtenir la limite de la suite. D'autres exemples de limites de suites sont également étudiés, tels que les suites qui tendent vers l'infini ou vers des limites finies. Dans ces cas, il est souvent nécessaire d'utiliser le théorème de comparaison ou le théorème des gendarmes pour déterminer la limite de la suite. En résumé, ces méthodes permettent de déterminer les limites de suites de manière efficace et rapide. Il est également recommandé d'utiliser l'encadrement lorsque les termes de la suite sont des puissances négatives, des sinus ou des cosinus.

Téléscopage !

Le cours aborde la notion de limites de suites définies comme des sommes de termes d'autres suites. Dans un premier temps, il faut déterminer la limite de la suite Un, qui est égale à 1/n. On obtient que Un tend vers 0. Ensuite, il est demandé de montrer que pour toute valeur de n, Un est égale à 1/n - 1/(n+1). Il est conseillé de prendre la manière la plus simple pour démontrer cette équivalence, en partant de 1/n - 1/(n+1) et en simplifiant jusqu'à obtenir Un. En utilisant la question précédente, on peut ensuite calculer la somme Sn de la suite Un. En utilisant la version de Un obtenue précédemment, on obtient une somme télescopique, où les termes se simplifient les uns les autres. La somme Sn converge alors vers 1. En déduisant la limite de Sn lorsque n tend vers l'infini, on obtient que cette limite converge vers 1.

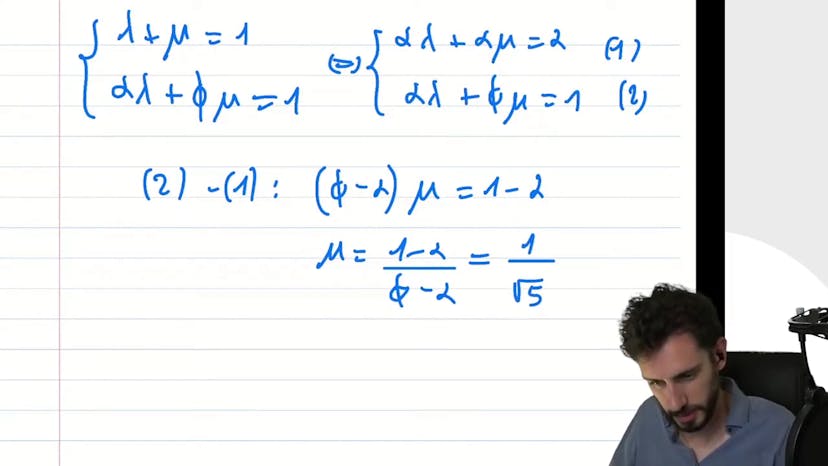
Prépa : Fibonacci

La suite de Fibonacci et le nombre d'or sont définis par une relation de récurrence où chaque terme est la somme des deux précédents. Pour calculer les termes de la suite, il faut connaître les deux premiers termes (u0 et u1). On cherche ensuite à trouver des réels (a, b, lambda, mu) tels que chaque terme puisse être exprimé sous forme d'une combinaison linéaire de sommes géométriques. Plutôt que de chercher à résoudre les équations directement, on peut analyser cette relation en se demandant s'il existe une seule somme géométrique qui pourrait vérifier cette relation, puis vérifier s'il y en a plus. En utilisant cette approche, on trouve que les valeurs possibles pour a et b sont les suivantes : a = (1 + √5)/2 (le nombre d'or) et b = (1 - √5)/2. En utilisant ces valeurs, on peut résoudre les 2 équations avec les 2 inconnus lambda et mu et trouver leurs valeurs respectives. Ainsi, on obtient les valeurs exactes pour les termes de la suite de Fibonacci. En résumé, la suite de Fibonacci peut être exprimée sous forme de sommes géométriques en utilisant les valeurs a et b (lesquelles sont calculées à partir du nombre d'or), et les constantes lambda et mu sont déterminées par les équations provenant des conditions initiales de la suite.

Intro Convergence

Bienvenue dans ce dernier sujet du chapitre sur les suites, les théorèmes de convergences. Les théorèmes de convergence nous permettent de mieux comprendre et analyser certaines suites qui peuvent sembler complexes. Nous pouvons observer que certaines fractions sont divisées par des valeurs de plus en plus grandes, ce qui peut sembler rendre la suite difficile à gérer. Cependant, si nous examinons de plus près, nous pouvons remarquer que ces nombres restent très petits. Malgré leur apparence complexe, ils se rapprochent de zéro. Nous pouvons également le voir graphiquement grâce à la fonction sinusex sur x et la suite sinusène sur n. Bien que la suite oscille, elle s'approche de plus en plus de zéro. Les théorèmes de convergences nous permettent d'analyser ces suites complexes en les comparant à des suites plus simples pour en tirer des conclusions. Parmi les théorèmes importants qui nous aideront à trouver les limites des suites, il y a le théorème de comparaison et le théorème de gendarme. Le premier est utilisé pour démontrer que quelque chose tend vers l'infini, tandis que le second est utilisé pour montrer qu'une suite tend vers une limite finie. Nous verrons également quelques définitions telles que les suites minorées, majorées et bornées. Enfin, nous étudierons le théorème de convergence monotone, ainsi que des méthodes pratiques pour gérer les suites comportant des sinus ou des puissances négatives. Nous aborderons également un cas courant : les suites homographiques. Cette vidéo nous prépare également à la prochaine vidéo qui sera consacrée au théorème de comparaison. N'hésitez pas à poser vos questions dans la FAQ. À bientôt !

Théorème de comparaison - Illustration

Le théorème de comparaison en analyse mathématique est un outil puissant qui permet de simplifier les démonstrations en se basant sur des suites comparables. En effet, si on a une suite Vn qu'on ne sait pas traiter directement, mais qu'on peut comparer à une suite plus simple Un qui tend vers l'infini, alors on peut en déduire que Vn suit le même comportement. Par exemple, si on peut montrer que Vn est toujours plus grand que Un, et que Un tend vers l'infini, alors Vn aussi. Cela permet d'éviter des calculs compliqués avec des epsilon et d'autres paramètres peu attrayants. On peut ainsi conclure que Vn suit la même tendance que Un sans avoir à étudier en détail la forme particulière de Vn. Ce théorème est particulièrement utile lorsque la suite Vn a une forme difficile à manipuler, comme dans l'exemple donné, où Vn est égal à l'exponentielle de la racine de n² plus 1. Pour illustrer le théorème de comparaison, on prend l'exemple de racine de n² plus 1, qui est plus grand que racine de n² (n étant un entier). En utilisant l'exponentielle et en montrant que l'exponentielle de racine de n² plus 1 est plus grand que l'exponentielle de n, on peut conclure que Vn suit une croissance exponentielle et tend vers l'infini, car l'exponentielle de n est une suite géométrique de raison supérieure à 1. Ce théorème permet donc d'éviter des calculs complexes et de simplifier les démonstrations en se basant sur des comparaisons entre suites simples et suites plus complexes. Son utilité réside dans le fait qu'il permet d'aboutir à une conclusion sans avoir à étudier en détail la forme de la suite complexe.

Théorème de comparaison - démonstration

Dans ce cours, nous démontrons le théorème qui nous permet de simplifier nos démonstrations en utilisant une notation plus simple. Nous commençons par rappeler la définition de "tendre vers plus infini" pour une suite. Ensuite, nous traduisons l'énoncé du théorème en langage mathématique. Si la limite de la suite Un lorsque n tend vers plus infini est égale à plus infini, alors quelque chose se produit. Plus précisément, pour tout nombre positif A, il existe un rang N à partir duquel tous les termes de la suite Un sont supérieurs à A. Nous utilisons cette propriété pour conclure que pour tout N plus grand ou égal à un certain grand N, les termes de la suite Vn sont également supérieurs ou égaux à A. En résumé, pour tout nombre positif A, il existe un rang N à partir duquel tous les termes de la suite Vn sont supérieurs ou égaux à A. Cette conclusion correspond à la définition de la divergence vers plus infini. En utilisant cette démonstration, nous n'avons plus besoin d'utiliser les démonstrations avec les démonstrations en epsilon, en grand A, etc. Vous pouvez poser des questions dans la FAQ si vous avez des doutes.