Cours d'apprentissage en ligne

Suite majorée, minorée & Th de convergence monotone

Le cours porte sur les théorèmes de convergence. Il explique les définitions de base pour comprendre ces théorèmes. On dit qu'une suite est majorée lorsqu'elle est toujours bloquée par une certaine valeur et toutes les valeurs au-dessus. Il peut y avoir plusieurs valeurs bloquant la suite, mais il y en aura toujours une infinité. On dit qu'une suite est minorée lorsqu'elle ne peut pas descendre en dessous d'une certaine valeur. De même, il peut y avoir plusieurs valeurs bloquant la suite vers le bas. Lorsqu'une suite est à la fois majorée et minorée, on dit qu'elle est bornée. Le cours illustre ces concepts avec des exemples graphiques de suites bornées. Il explique également le théorème de convergence monotone, qui dit que si une suite est croissante et majorée, alors elle converge. Cependant, il souligne que ce théorème ne permet pas de trouver la limite de la suite, mais seulement de déterminer si elle converge. Le cours aborde également la réciproque du théorème de convergence monotone, qui est fausse. Il montre des contre-exemples de suites qui convergent sans être croissantes ou décroissantes. Il insiste sur l'importance de comprendre ces contre-exemples pour ne pas se faire piéger lors des exercices ou des questions de cours.

Th convergence monotone - démo

Dans cette vidéo, on fait une démonstration du théorème de convergence monotone dans le cas où on a une suite croissante non majorée. On explique que si la suite croissante n'est jamais bloquée et tend à augmenter constamment, alors elle tend vers plus l'infini. On donne la définition formelle de la convergence vers plus l'infini et on montre qu'elle est quasiment identique à la démonstration faite précédemment. On commence en fixant un nombre positif A. Ensuite, on démontre que pour ce A fixé, il existe toujours un certain rang à partir duquel la suite est au-dessus de A, c'est-à-dire que tout grand A finira par se faire dépasser. On combine le fait que la suite n'est pas majorée avec le fait qu'elle est croissante pour montrer que pour tout N au-dessus d'un certain rang P, chaque terme de la suite sera plus grand que A. Ainsi, on a montré que pour tout A fixé, la suite finira toujours par être au-dessus de A, ce qui correspond à la définition de convergence vers plus l'infini. On conclut en disant qu'on a démontré le théorème et en laissant les spectateurs sur cette note, en les invitant à revenir pour la prochaine vidéo.

Encadrer sin(n)

Dans ce cours, nous appliquons les théorèmes de convergence aux fonctions sinus et moins 1 puissance n. Nous étudions la suite un qui est égale à n plus 2 fois sin n. L'exercice nous demande de montrer que pour tout n, un est supérieur à n-2. Pour cela, nous utilisons l'encadrement du sinus entre -1 et 1. Puis nous multiplions par 2 et ajoutons n pour obtenir un. Ainsi, un est compris entre n-2 et n+2. Ce qui nous intéresse vraiment, c'est la partie où un est supérieur à n-2. En utilisant la limite usuelle, nous montrons que n-2 tend vers moins l'infini et que un est plus grand qu'une suite qui tend vers l'infini. Donc, par comparaison, un tend vers l'infini. Dans le deuxième exemple, nous avons la suite Vn qui est égale à moins n carré moins n plus moins 1 puissance n. Nous encadrons encore une fois le moins 1 puissance n entre -1 et 1. En analysant la suite, nous constatons que le terme dominant est moins n carré. Ainsi, le terme moins 1 puissance n ne nous gêne pas beaucoup. Nous démontrons cela par l'encadrement, en ajoutant moins n carré moins n à la suite Vn. Finalement, nous obtenons que Vn est inférieur à une suite qui tend vers moins l'infini. En factorisant et en examinant les limites, nous concluons que Vn tend vers moins l'infini. Ainsi, ces deux exemples nous montrent comment utiliser l'encadrement pour des suites impliquant le sinus ou moins 1 puissance n.

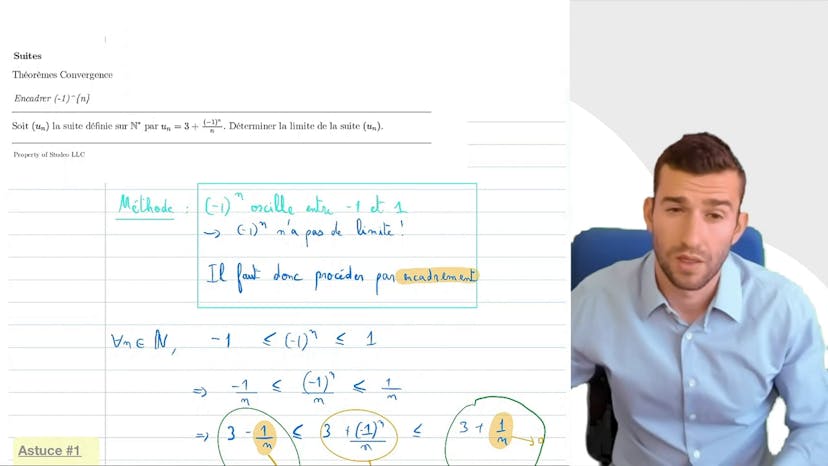
Encadrer (-1)^n

Dans ce cours, nous avons étudié une autre type de suite nécessitant un encadrement. Il s'agit des suites où il y a un "-1 puissance n" inclus. Dans ce cas, il n'y a pas de limite pour "-1 puissance n", donc nous utilisons l'encadrement pour déterminer la limite de la suite UN. Dans ce cas précis, UN est égal à 3 plus "-1 puissance n sur n". En raison du terme "-1 puissance n sur n", qui tend vers 0 en raison du facteur "sur n", nous pouvons voir que UN tend vers 3. Nous prouvons cela par encadrement. En partant de l'encadrement de "-1 puissance n", nous multiplions ensuite par un sur n, qui est positif, ce qui ne change pas le sens des inégalités, et nous ajoutons 3. Ainsi, nous avons 3 moins 1 sur n, qui est plus petit que UN, qui est plus petit que 3 plus 1 sur n. Par conséquent, le terme de gauche tend vers 3, tout comme le terme de droite. Selon le théorème d'encadrement, nous en concluons que UN tend vers 3. Il est important de souligner que le théorème d'encadrement permet non seulement de prouver la convergence, mais aussi de trouver la limite, ce qui en fait un théorème très puissant. Grâce à l'encadrement, nous avons donc montré que UN tend vers 3.

Exo TRÈS classique

Dans cette leçon, nous avons étudié une méthode pour trouver la limite d'une suite qui est une fonction rationnelle. Nous avons examiné le cas où le degré du numérateur est égal au degré du dénominateur, et la limite est alors le quotient des coefficients dominants de ces deux polynômes. Cependant, au lieu de nous intéresser à la limite elle-même, nous avons montré des résultats préliminaires tels que la majoration et la croissance de la suite, à partir desquels nous pouvons conclure sur sa convergence en utilisant les théorèmes de convergence. Dans le premier exercice, nous nous sommes intéressés à la majoration de la suite Un=n-1 / (n+4) et avons montré qu'elle est inférieure à 1. Ensuite, nous avons étudié la monotonie de la suite, en regardant Un+1 - Un, et avons conclu que la suite est strictement croissante. Ensuite, nous avons montré que la suite est à la fois croissante et majorée, ce qui implique qu'elle est convergente. Cependant, nous ne pouvons pas déduire la limite à partir de ces résultats. Ensuite, nous avons examiné un autre exemple avec la suite Un=2n-2 / (n+4). En utilisant la méthode précédente, nous avons montré que la suite est majorée par 2 et que la suite est strictement croissante. Cela implique que la suite est convergente, mais encore une fois, nous ne pouvons pas conclure sur la limite. En conclusion, cette méthode nous permet de montrer la convergence d'une suite rationnelle en montrant sa majoration et sa croissance, mais elle ne nous permet pas de déterminer la limite. Il est important de noter que la limite n'est pas nécessairement le majorant trouvé, et que la suite peut converger vers une valeur inférieure.

Introduction Limites

Lors de l'étude des limites de fonctions, on peut s'inspirer de ce qui a été fait pour les suites. Une suite converge lorsque ses termes semblent se rapprocher d'une valeur. Les fonctions sont plus complexes que les suites car elles portent sur l'ensemble des réels, contrairement aux suites qui ne portent que sur les entiers. Les fonctions peuvent avoir différents types de limites, comme se rapprocher d'un réel, tendre vers l'infini ou osciller. On utilise un vocabulaire plus étendu lorsqu'on parle de limites de fonctions. Les limites peuvent être étudiées en l'infini, c'est-à-dire lorsque la variable tend vers l'infini, ou en un réel particulier. Il y a également des cas où il n'y a pas de limite. Des exemples graphiques sont utilisés pour illustrer ces différents cas. On introduit également la notion d'asymptote, qui est une droite vers laquelle la fonction semble tendre. Dans ce chapitre, nous étudierons les définitions et les exemples de limites, ainsi que les méthodes pour les calculer. Nous utiliserons l'analyse graphique, la factorisation et les définitions pour déterminer les limites. Il faudra aussi connaître les concepts d'asymptotes horizontales et obliques.

En l'infini, limites finies et infinies

La séquence présente deux définitions des limites lorsque x tend vers l'infini en mathématiques. La première définition concerne les fonctions qui tendent vers l'infini lorsque x devient de plus en plus grand. On dit qu'une fonction tend vers l'infini si, quel que soit le plateau Y choisi, la fonction finit toujours par dépasser ce plateau. La deuxième définition concerne les fonctions qui tendent vers un réel L. Dans ce cas, toutes les valeurs de la fonction finissent par être comprises dans un intervalle autour de L, peu importe la taille de cet intervalle. Ces définitions sont similaires à celles utilisées pour les suites. Il est important de préciser que lorsque x tend vers plus l'infini, afin de distinguer les autres valeurs de x. Les exemples graphiques sont présentés pour illustrer ces définitions. Il est conseillé de comprendre ces concepts, car ils sont utilisés dans des exercices mathématiques et peuvent rapporter des points précieux. N'hésitez pas à poser des questions si nécessaire.

Les asymptotes horizontales

Lorsque X tend vers l'infini, une asymptote est une droite vers laquelle la courbe de la fonction F se rapproche. Cela se produit lorsque la limite de F lorsque X devient très grand converge vers un réel appelé L. Il est important de rappeler qu'il existe une asymptote à la courbe de F et non à la fonction F elle-même. Une petite erreur courante à éviter est de dire que la droite se colle à la fonction F au lieu de dire qu'elle se colle à la courbe de la fonction F. Un exemple d'asymptote horizontale est une fonction de la forme 1/X, où la droite Y égale 3 est asymptote à la courbe de F. Il peut y avoir des asymptotes croissantes ou décroissantes selon le côté où la courbe se rapproche de la droite. Il est également possible d'avoir une asymptote pour des fonctions comme le sinus. L'asymptote est la droite vers laquelle la courbe de F se rapproche infiniment proche. C'est une notion liée à la limite et intuitive.

Bonus : Les asymptotes obliques

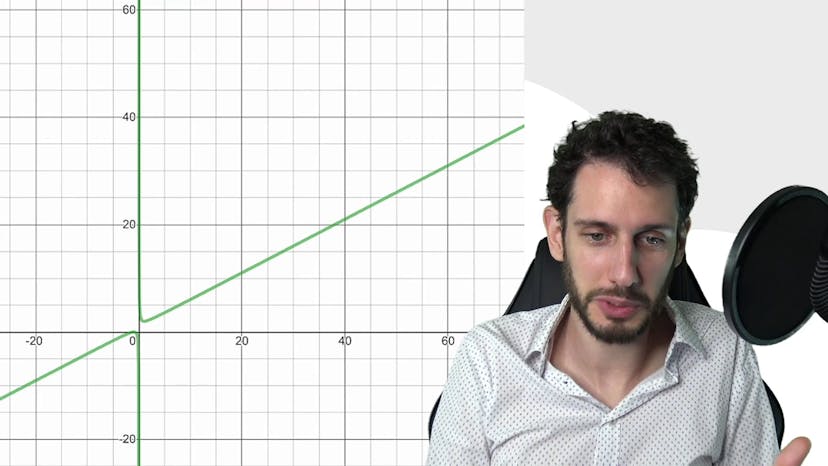
Dans ce cours, nous abordons le concept d'asymptote oblique qui se produit lorsque l'asymptote d'une courbe n'est plus horizontale mais inclinée. Nous considérons une fonction f définie sur un ensemble de définitions (df), dont la courbe cf représente la fonction f. Lorsque la différence entre la valeur réelle f2x et la droite ax + b tend vers 0, cela signifie que la courbe se rapproche de la droite oblique ax + b. Contrairement aux asymptotes horizontales où f2x tend vers une valeur réelle l, ici f2x tend vers plus l'infini car elle suit une droite affine. Il est important de savoir détecter et comprendre ce type de situation, car cela se produit fréquemment dans les exercices. Un exemple d'illustration est donné, montrant comment la courbe verte se rapproche de plus en plus de la droite rouge à mesure qu'on se rapproche de l'infini. Lorsque l'on dézoome, on constate que la courbe est pratiquement une droite. Dans certaines situations, cela peut également se produire de l'autre côté de la courbe. La différence entre les valeurs des courbes verte et rouge tend vers 0, indiquant un rapprochement. Ce cours a pour objectif de clarifier le concept d'asymptote oblique.

En un point réel, limite infinie

Lorsqu'on parle de limite de fonction avec X qui tend vers un réel A, on distingue deux cas principaux : 1. La fonction F peut finir par partir vers plus ou moins l'infini. 2. La fonction F peut converger vers une valeur finie. Dans le cas où la fonction F converge vers une valeur finie, cela signifie que la courbe de la fonction suit son cours normal et s'approche d'une valeur L. Cette notion est appelée la continuité. Par exemple, la limite de X + 3 lorsque X tend vers 2 est égale à 5. Cependant, il existe des cas plus complexes, comme celui de la fonction sinus X sur X où la limite en 0 est indéterminée (0/0). Dans ce cas, on exclut 0 de l'ensemble de définition de la fonction pour éviter une division par 0. Malgré cela, il est possible de démontrer que la limite de cette fonction en 0 est égale à 1. En ce qui concerne la limite infinie, on peut l'aborder en utilisant la notion de plateau. Lorsque la fonction F tend vers plus l'infini, cela signifie que la fonction ne peut être bloquée par aucun plateau de données. Par exemple, si on prend une hyperbole, peu importe la taille du plateau choisi, la fonction finira par le dépasser lorsqu'on se rapproche de plus en plus d'une valeur donnée. Si la limite à gauche ou à droite de F(x) lorsque X tend vers A est infinie, on parle d'une asymptote verticale en X égale à A. En résumé, lorsque X tend vers un réel A, il peut y avoir plusieurs cas de limite de fonction, dont certains peuvent être représentés par des asymptotes verticales ou horizontales.

Analyse graphique

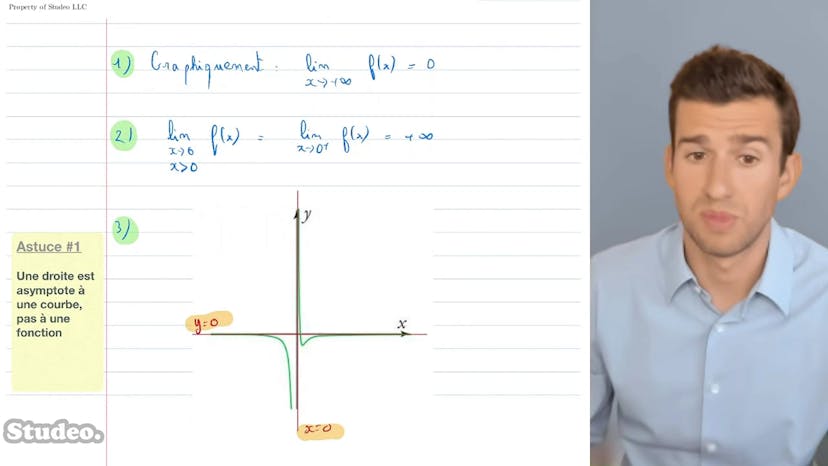
Bonjour à tous ! Dans ce cours, nous allons aborder la notion des limites des fonctions à travers une analyse graphique. Nous examinons une fonction tracée et tentons de déterminer ses limites. Lorsque nous observons le graphique, nous constatons que lorsque x tend vers l'infini, la fonction tend vers 0. C'est notre première observation. Ensuite, lorsque x tend vers 0 par une valeur positive, nous remarquons que la courbe s'élève vers l'infini. Cela nous conduit à conclure que la fonction admet deux asymptotes, une verticale en x=0 et une horizontale pour les valeurs positives et négatives infinies. Lorsqu'on nous demande les équations des asymptotes, nous savons que les droites horizontales sont de la forme y=a, tandis que les droites verticales sont de la forme x=a. Dans ce cas, l'équation pour l'asymptote horizontale est y=0 et pour l'asymptote verticale, c'est x=0. Une remarque importante à faire est qu'on parle d'une droite comme étant l'asymptote d'une courbe et non de sa fonction. Enfin, il est tout à fait possible qu'une droite soit asymptote en deux endroits, comme c'est le cas ici où l'asymptote horizontale est présente pour les valeurs positives et négatives infinies. Voilà pour cette méthode d'introduction. Si vous avez des questions, n'hésitez pas à les poser.