 All subjects
All subjects
 All subjects
All subjects
Maths SM&SP
Analyse
2BAC SM Maroc

Déf fondamentale
Le cours traite du logarithme et de ses propriétés. La fonction logarithme, notée ln, est définie sur l'ensemble des réels strictement positifs. Elle associe à chaque nombre réel positif x, l'unique solution de l'équation exponentielle E^(2y) = x. On utilise le symbole "log" pour indiquer la solution à l'équation E^(2y) = x, ce qui revient à écrire log(x) = y. L'exponentielle de log(x) est toujours égale à x, et réciproquement, le logarithme de l'exponentielle de x est égal à x. Il existe quelques valeurs particulières, tels que log(1) = 0, log(e) = 1 et log(1/e) = -1. Il faut faire attention à ne pas confondre la racine carrée de x², qui donne la valeur absolue de x, avec le logarithme de x, qui est défini uniquement pour les x positifs. La prochaine vidéo abordera d'autres notions liées au logarithme.
Maths SM&SP
Analyse
2BAC SM Maroc

Simplifier des expressions
Bienvenue dans le monde du logarithme ! Dans ce cours, nous allons aborder les propriétés importantes pour résoudre des inéquations avec l'exponentiel et le logarithme. Nous allons prendre ces propriétés une par une et les résoudre.
La première propriété est assez simple : ln(x) = 2. Avant de résoudre cette équation, il est important de noter que les fonctions exponentielle et logarithme sont croissantes, ce qui joue un rôle important dans les inégalités. Lorsque nous utilisons le logarithme naturel, nous devons toujours vérifier que le nombre à l'intérieur est strictement positif, car ln est défini uniquement pour les réels positifs. En revanche, pour l'exponentielle, il n'y aura jamais de problème. Donc, dans ce cas, nous pouvons simplement utiliser l'exponentielle des deux côtés de l'équation et obtenir x = e^2 comme solution.
Passons maintenant à la deuxième propriété : e^x + 1 = 5. Cette fois-ci, nous utilisons le logarithme pour résoudre l'équation. Comme e^x + 1 est toujours positif et que 5 est strictement positif, nous pouvons utiliser le logarithme des deux côtés de l'équation et obtenir x + 1 = ln(5) comme solution.
La troisième propriété est un peu plus complexe : 3ln(x) - 4 = 8. Encore une fois, il est important de noter que l'équation est définie uniquement pour les réels positifs, donc nous devons faire attention. Nous isolons d'abord le ln(x) et utilisons ensuite l'exponentielle pour obtenir x = e^(4/3) comme solution.
Passons maintenant aux inéquations. Dans ln(6x) - 1 > 2, nous devons vérifier l'ensemble de définition de l'inéquation, qui est 1/6 + l'infini, car l'intérieur du ln doit être strictement positif. En utilisant l'exponentielle, nous obtenons 6x - 1 > e^2, ce qui nous donne x > e^2 + 1/6. Nous devons toujours vérifier si cette solution respecte l'hypothèse de départ, ce qui est le cas ici.
Dans e^x + 5 > 4e^x, nous devons d'abord rassembler les exponentielles pour pouvoir utiliser le logarithme. Cela nous donne e^x < 5/3. En utilisant le logarithme, nous obtenons x < ln(5/3).
Dans ln(x-3) + ln(9-x) = 0, nous pouvons rassembler les logarithmes pour obtenir ln[(x-3)(9-x)] = 0. En utilisant l'exponentielle, nous obtenons l'équation carrée classique (x-3)(9-x) = 0. Après avoir résolu cette équation, nous trouvons deux solutions : x = 6 + racine(8) et x = 6 - racine(8). Cependant, nous devons vérifier si ces solutions sont incluses dans l'ensemble de définition de l'équation, c'est-à-dire si elles sont supérieures à 3 et inférieures à 9.
Enfin, dans ln(3-x) - ln(x+1) < 0, nous devons d'abord trouver l'ensemble de définition de l'inéquation, qui est -1 < x < 3. En rassemblant les logarithmes, nous obtenons ln[(3-x)/(x+1)] < 0. Multipliant par (x+1), qui est toujours positif, nous obtenons 3-x < 0, c'est-à-dire x > 2. En intersecant ces deux intervalles, nous trouvons que la solution est 2 < x < 3.
Donc, en résumé, lorsque nous résolvons des équations et des inéquations avec le logarithme et l'exponentiel, nous devons toujours prendre en compte l'ensemble de définition de l'équation ou de l'inéquation. Il est également important de rassembler les termes en logarithmes ou en exponentielles autant que possible, et de composer avec la fonction réciproque au dernier moment. N'oubliez pas de prendre en compte les signes lorsque vous divisez ou multipliez par une expression dont le signe n'est pas clair.
J'espère que ce résumé vous a aidé à comprendre les principes de base de la résolution d'équations et d'inéquations avec le logarithme et l'exponentiel !
Maths SM&SP
Analyse
2BAC SM Maroc

Équations Inéquations
Ce cours concerne la résolution d'une inéquation avec le logarithme. L'équation à résoudre est 3-ln(2x + 1)/2 > 1. Tout d'abord, il faut déterminer l'ensemble de définition de l'inéquation, qui est -1/2 à l'infini pour (2x + 1). Ensuite, pour isoler le terme en ln, on déplace le -3 de l'autre côté de l'équation, ce qui devient -2. En multipliant par -1, on change le sens de l'inégalité. A ce stade, le ln est isolé et on peut composer avec l'exponentiel. On obtient 2x + 1 < e^4. Cela permet d'isoler x, qui équivaut à (e^4 - 1)/2. On vérifie ensuite si cette solution se trouve dans l'intervalle initial (-1/2, infini). Finalement, l'intervalle solution est l'intersection entre l'intervalle initial et la solution obtenue, soit (-1/2, (e^4 - 1)/2). Il est important de prendre en compte l'ensemble de définition et de faire attention aux intervalles de résolution.
Maths SM&SP
Analyse
2BAC SM Maroc

Exposant=Inconnue ?
Ce cours aborde l'utilisation de l'exponentiel et du logarithme pour résoudre des inéquations où l'inconnu est un exposant. Ces types de calculs sont souvent utilisés en physique, notamment en radioactivité pour déterminer la durée nécessaire pour que 80% des atomes radioactifs disparaissent.
Pour résoudre ces inéquations, on utilise les lois géométriques et la définition de l'exponentiel pour les puissances. Lorsque l'exposant n'est pas un entier, on utilise la formule A puissance B = E de B ln de A. Ainsi, pour résoudre l'expression 1/5 à la puissance N, on utilise la formule E de N ln de 1/5.
En utilisant les propriétés du logarithme, on peut simplifier cette expression en -ln de 5. On obtient donc que 1/5 à la puissance N est inférieur à 0,01, ce qui peut être réécrit comme -N ln de 5 inférieur à N ln de 0,01.
En multipliant par -1 et en divisant par ln de 5, on obtient N supérieur à ln de 0,01 sur ln de 5. Pour vérifier la cohérence des signes, on peut observer que la suite géométrique 1/5 tend vers 0 lorsque N devient grand, ce qui confirme que l'expression est inférieure à 0,01 à partir d'un certain ordre.
Dans un autre exemple, pour résoudre l'expression 1,22 à la puissance N supérieur à 10 puissance 5, on utilise la formule E de N ln de 1,22. En simplifiant l'expression, on obtient N supérieur à 5 ln de 10 sur ln de 1,22. Encore une fois, la cohérence des signes est vérifiée, ce qui confirme la résolution de l'inéquation.
En résumé, la méthode consiste à revenir à la définition de la puissance avec l'exponentiel et le logarithme, puis à appliquer les méthodes précédentes pour résoudre les inéquations.
Maths SM&SP
Analyse
2BAC SM Maroc
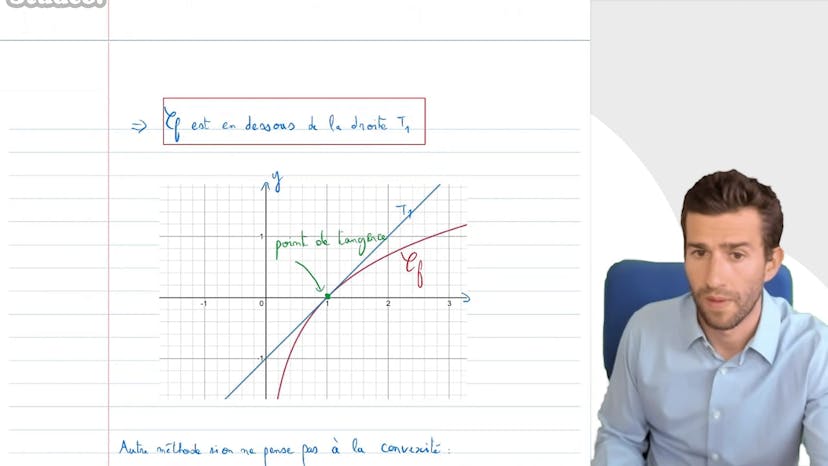
Courbe et Tangentes
En résumé, ce cours porte sur l'étude de la tangente au point d'abscisse 1 de la fonction logarithme. La fonction ln est dérivable sur R étoile plus, avec une dérivée de f prime(x) égale à 1/x. En utilisant la formule de l'équation de la tangente, on obtient l'équation y = x-1. On aborde ensuite la position relative de la courbe par rapport à la tangente en utilisant la notion de convexité et de concavité de la fonction. On détermine que la fonction logarithme est concave, ce qui signifie que la courbe est en dessous de toutes ses tangentes, y compris celle au point d'abscisse 1. On introduit également une autre méthode en étudiant la différence entre la fonction logarithme et la tangente, en utilisant une fonction auxiliaire g(x) = ln(x) - x + 1. En analysant les variations de g, on déduit que g(x) est toujours inférieur à 0, ce qui confirme que la fonction logarithme est en dessous de sa tangente en x = 1. Il est recommandé de privilégier la méthode de la concavité pour simplifier les calculs. En conclusion, la tangente la plus connue de la fonction logarithme au point d'abscisse 1 a pour équation y = x-1. Il est important de reconnaître cette tangente dans les exercices et de l'utiliser dans les calculs.
Maths SM&SP
Analyse
2BAC SM Maroc
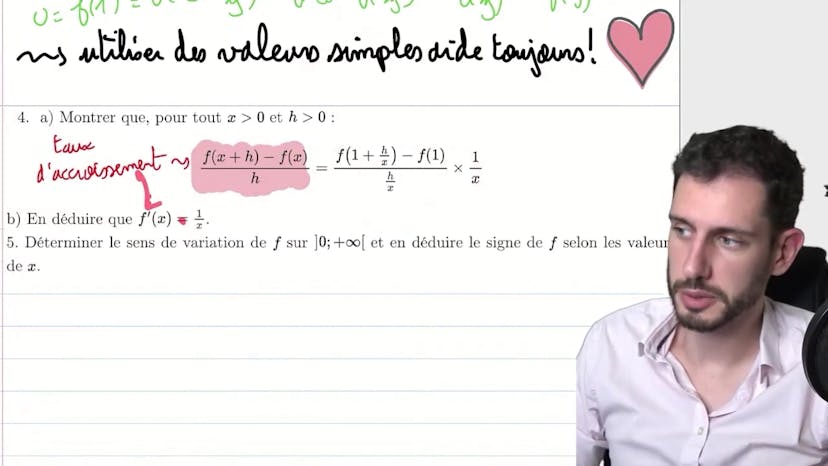
On redécouvre le log ?!
Dans ce cours, nous cherchons à déterminer les fonctions qui vérifient les conditions suivantes : f2ab = f2a + f2b et f'(1) = 1.
Tout d'abord, nous reconnaissons la relation fonctionnelle du logarithme et la dérivée du logarithme en 1. Nous allons redémontrer ces propriétés.
Nous commençons par supposer que la fonction f est définie en 0. En remplaçant a et b par 0 dans la relation donnée, nous obtenons 2f(0) = f(0), ce qui implique que f(0) = 0.
Pour trouver une contradiction, nous prenons a différent de 0 et b égal à 0. Cela nous donne f(a) = 0. Comme f(0) = 0, nous en concluons que f est égale à 0 pour tous les réels possibles, ce qui contredit la condition de non-nulle de f.
Nous pouvons donc démontrer que la fonction f ne peut pas être définie en 0. Par conséquent, nous allons considérer des fonctions définies sur 0+.
Ensuite, nous montrons que f(1) = 0 en substituant a et b par 1 dans la relation donnée.
Enfin, nous démontrons que f(x/y) = f(x) - f(y) en utilisant une astuce similaire à la démonstration du logarithme de a/b = log(a) - log(b).
Dans la suite de l'exercice, nous devons montrer que f'(x) = 1/x pour tout x positif et h positif.
Nous reconnaissons qu'il s'agit d'un taux d'accroissement et que nous devons montrer une propriété numérique avant de le traiter comme un taux d'accroissement en l'exploitant.
En utilisant les relations précédentes, nous parvenons à démontrer que f'(x+h) - f'(x) = (1 + h/x) - 1/x = h/x².
En prenant la limite de cette expression lorsque h tend vers 0, nous obtenons f'(x) = 1/x.
Enfin, nous déterminons le sens de variation de f sur 0+ en utilisant le fait que f'(x) est toujours positif.
En conclusion, nous avons retrouvé les propriétés du logarithme à partir des conditions f2ab = f2a + f2b et f'(1) = 1.
Maths SM&SP
Analyse
2BAC SM Maroc

Une nouvelle définition de l'exp
Dans ce cours, il est expliqué que le logarithme a une propriété importante : log de A puissance N est égal à N fois log de A. Cette propriété permet de simplifier les expressions avec des puissances élevées. Lorsque l'expression devient compliquée, il suffit d'appliquer le logarithme pour éliminer la puissance.
Il est ensuite demandé de montrer que l'expression log de U N est bien définie, c'est-à-dire que ce qui est à l'intérieur du logarithme est strictement positif. En divisant par N, on obtient l'inégalité 1 + A/N > 0. En élevant ensuite cette expression à la puissance N, on montre que la condition est bien vérifiée.
Ensuite, il est demandé de calculer la limite de log de U N. En utilisant une propriété du logarithme, log de 1 + U divisé par U tend vers 1 lorsque U tend vers 0. Il est alors nécessaire de transformer l'expression log de U N en log de 1 + A/N divisé par A/N. En simplifiant cette expression, on obtient que la limite du logarithme de U N est égale à A. On en déduit alors que l'exponentielle de log de U N tend vers U N, ce qui répond à la question posée.
En conclusion, ce cours aborde les propriétés du logarithme et montre comment les utiliser pour simplifier les expressions et calculer des limites.
Maths SM&SP
Analyse
2BAC SM Maroc

Dérivabilité et Variations
Le cours concerne l'étude d'une fonction faisant intervenir le logarithme. La fonction en question est ln(2x + 1) / ln(2x - 1). Elle est définie sur l'intervalle (0, +∞) exclu e, où e est exclu en raison de l'annulation du dénominateur en e.
Pour étudier cette fonction, on utilise la dérivée de la fonction, qui est (u'v - uv') / v², avec u = ln(2x + 1) et v = ln(2x - 1). En effectuant les calculs, on obtient la dérivée simplifiée -2x / (ln(2x - 1))². Étant donné que le dénominateur est strictement positif sur (0, +∞), la dérivée est strictement négative sur cet intervalle.
Cependant, il y a une valeur interdite en e, ce qui signifie que la fonction n'est pas décroissante sur tout l'intervalle. En réalité, elle décroît sur l'intervalle (0, e) et décroît sur (e, +∞). Il y a donc une discontinuité dans la fonction aux alentours de e.
Pour obtenir un tableau de variation complet, on étudie les limites de la fonction en 0, e+, e- et +∞. En utilisant la méthode de factorisation par le terme dominant, on trouve que la limite de la fonction en 0 est égale à 1, tout comme la limite en +∞.
Quant aux limites en e+, la fonction tend vers +∞, et en e-, elle tend vers -∞.
En traçant la fonction, on observe une asymptote verticale à x = e (et non y = e) en raison de la valeur interdite, ainsi qu'une asymptote horizontale à y = 1, lorsque x tend vers l'infini.
Il est important de noter que la fonction n'est décroissante que sur les intervalles (0, e) et (e, +∞), et il y a un saut de moins l'infini à plus l'infini au niveau de la valeur interdite e.
Ceci conclut la méthode utilisée pour l'étude de cette fonction utilisant le logarithme. En cas de questions supplémentaires, vous pouvez vous référer à la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Croissance Comparée
Dans cette transcription de vidéo, on étudie la fonction f(x) = 3-x + 2ln(2x).
Tout d'abord, on dérive la fonction pour trouver son signe : f'(x) = -1 + 2x. On veut trouver les valeurs de x pour lesquelles f'(x) est supérieur à 0. En isolant x, on obtient que x doit être supérieur à 1. Donc f'(x) est positif sur [1, +∞).
Ensuite, on calcule f(2) = 1 + 2ln(2) = 1 + ln(4) = ln(4) + 1.
Pour étudier les limites de f, on utilise la technique de la croissance comparée. On factorise par un terme prédominant, x, et on obtient que lorsque x tend vers plus l'infini, f(x) tend vers moins l'infini, et lorsque x tend vers 0, f(x) tend vers -∞.
Grâce à ces informations, on peut construire le tableau de variation de f. On observe que f est décroissante sur [0,2] et croissante sur (2, +∞). Elle atteint son maximum en 2 où f(2) = ln(4) + 1.
Ensuite, on étudie la convexité de f en calculant la seconde dérivée, f''(x) = -1/x^2. On trouve que f''(x) est strictement inférieur à 0 sur R étoile plus, ce qui signifie que f est concave sur R étoile plus tout entier.
Pour plus d'informations, il est recommandé de consulter l'FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Ln : Limites
Dans ce cours, nous étudions des limites faisant intervenir la fonction ln et utilisons la technique de factorisation par le terme prédominant pour simplifier les calculs.
Dans la première limite, nous avons l'expression 2ln(2x²)-5ln(2x)±1. En factorisant par ln(2x²), nous obtenons 2 + 5/ln(2x) + 1/ln²(2x), qui tendent toutes vers 0. Ainsi, la limite de cette expression est plus l'infini.
Dans la seconde limite, nous avons ln(√x) / ln(2x) lorsque x tend vers l'infini. Cette forme est indéterminée, donc nous utilisons les propriétés du logarithme pour simplifier l'expression. En utilisant ln(AB) = ln(A) + ln(B), nous transformons ln(√x) en 1,5ln(x). Nous factorisons ensuite par 1,5 pour obtenir (xln(x) / ln(2x))(1 + ln(2)/ln(x)). Cette expression tend vers 1,5.
Enfin, dans la dernière limite, nous calculons x²ln(x) lorsque x tend vers 1. Nous posons grand x = x - 1 pour ramener la limite à une forme plus familière, à savoir xln(x). Comme x tend vers 1, grand x tend vers 0, et nous pouvons simplifier l'expression en x(xln(x)). Nous savons que xln(x) tend vers 0, donc la limite recherchée est égale à 0.
En résumé, pour calculer ces limites avec la fonction ln, nous utilisons la factorisation par le terme prédominant et les propriétés du logarithme.
Maths SM&SP
Analyse
2BAC SM Maroc

Dériver ln(u)
Dans ce cours, on apprend qu'il faut faire attention lorsqu'on utilise le logarithme, car il n'est défini que sur Réactoire+. Il est important de regarder l'ensemble de définition d'une expression qui fait intervenir le logarithme. On se focalise ensuite sur la détermination de l'ensemble de définition d'une fonction avec le logarithme et le calcul de sa dérivée.
On commence par l'exemple de la fonction f(x) = ln(8x-4). On détermine que cette fonction est définie et dérivable sur l'intervalle [1.5, +∞[. On calcule ensuite sa dérivée qui est égale à 2/(2x-1).
Ensuite, on étudie la fonction f(x) = ln(x²+x+1), qui est définie et dérivable sur tout R. On calcule sa dérivée qui est égale à 2x/(x²+x+1).
On aborde également la fonction f(x) = ln(u/v), où l'on doit étudier le signe pour savoir quand elle est strictement positive. On détermine que cette fonction est strictement positive sur l'intervalle ]-∞,-2[ ∪ ]1,+∞[. On calcule ensuite sa dérivée qui est plus complexe, en utilisant la formule de dérivation des fonctions composées.
Enfin, on étudie la fonction f(x) = ln(e^x), qui est définie et dérivable sur l'intervalle ]0,+∞[. On calcule sa dérivée qui est égale à 1.
Il est important de retenir qu'il faut toujours vérifier l'ensemble de définition lorsqu'on utilise le logarithme dans une expression.
Maths SM&SP
Analyse
2BAC SM Maroc
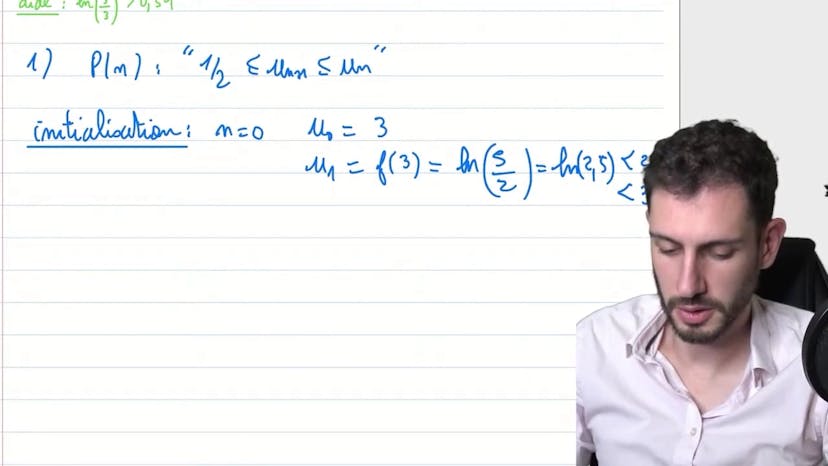
Fonction et suite récurrente associée
Dans ce cours, nous étudions une fonction définie par une fraction rationnelle avec un degré de 1 au-dessus et un degré de 1 en dessous de la barre de fraction. Le domaine de définition de cette fonction est de 0 à l'infini. Nous déterminons ensuite la limite de cette fonction lorsque x tend vers l'infini, ce qui nous permet de conclure que la limite est égale au logarithme de 3. Nous montrons également que la dérivée de la fonction est égale à 3x + 3. Ensuite, nous abordons l'étude d'une suite définie par récurrence à l'aide de cette fonction. Nous démontrons par récurrence que la suite est décroissante et minorée par un demi. Enfin, nous expliquons le théorème qui permet de conclure que si une suite est décroissante et minorée, alors elle converge.
Maths SM&SP
Analyse
2BAC SM Maroc

Un classique de BAC : étude de fonction en 2 temps
Le cours aborde un exercice classique d'étude de fonctions où l'on nous donne deux fonctions, F et G, et nous devons les étudier. L'objectif est de déterminer la dérivée de F et d'étudier ses limites.
Dans un premier temps, nous devons déterminer l'ensemble de définition de G et calculer ses limites aux bornes de cet ensemble. L'ensemble de définition de G est l'ensemble des réels strictement positifs, car il y a un logarithme dans l'expression. En étudiant les limites de G, nous obtenons que G tend vers 1 en approchant de zéro depuis la droite et tend vers moins l'infini en approchant de l'infini.
Ensuite, nous devons étudier la dérivée de F et dresser son tableau de variations. La fonction F est dérivable car elle est la somme de deux fonctions dérivables. En calculant la dérivée de F, nous remarquons une expression similaire à celle de G. Nous utilisons cette observation pour déterminer le signe de la dérivée de F et dresser le tableau de variations. Nous obtenons que F est croissante de moins l'infini à un certain point alpha, puis décroissante. Les limites de F aux bornes de son ensemble de définition sont moins l'infini et zéro.
Enfin, nous devons résoudre l'équation F(x) = 0. Pour cela, nous utilisons le théorème des valeurs intermédiaires. Étant donné que F est continue, que 0 appartient à l'intervalle [-infini, 2] et que F est strictement décroissante sur cet intervalle, il existe une unique solution alpha telle que F(alpha) = 0.
En résumé, l'exercice consiste à calculer les limites de G et F aux bornes de leur ensemble de définition, à dresser les tableaux de variations des deux fonctions et à résoudre l'équation F(x) = 0 en utilisant le théorème des valeurs intermédiaires.


