 All subjects
All subjects
 All subjects
All subjects
Maths
Algèbre
MPSI/PCSI

Somme et intersections
Dans cette vidéo, nous allons analyser différentes propriétés sur une famille de vecteurs, en utilisant un petit QCM. La première question consiste à déterminer si l'ensemble des combinaisons linéaires des vecteurs U1, U2 et U3 est égal à l'ensemble des combinaisons linéaires de ces deux vecteurs. Pour répondre à cette question, nous devons d'abord comprendre que si la proposition est vraie, cela signifie que la famille de vecteurs est liée, ce qui implique que seul deux des vecteurs sont linéairement indépendants. Ensuite, nous devons analyser si le vecteur donné appartient à l'intersection de l'ensemble formé par les vecteurs U1 et U2 et l'ensemble des combinaisons linéaires de ces vecteurs. Enfin, la troisième question vise à déterminer si la combinaison des ensembles Vect(U1, U2) et Vect(U2, U3, U4) peut générer tous les éléments de R4. Il est important de remarquer que la présence du symbole "+" sans le symbole "⊕" suggère qu'il peut y avoir des redondances entre les deux ensembles. Dans cette analyse, nous utilisons les propriétés des combinaisons linéaires et faisons quelques manipulations avec les vecteurs afin de répondre aux questions posées. Il est recommandé d'acquérir de la pratique pour maîtriser ces manipulations de manière efficace. Pour la première question, nous pouvons remplacer U1 par U1 + U2 ou U1 - U2 pour obtenir un résultat plus clair. Pour la deuxième question, nous vérifions si le vecteur donné est une combinaison linéaire de U1 et U2. Pour la troisième question, nous utilisons un argument de dimension pour déterminer si la somme des deux ensembles génère tout l'espace R4. En utilisant ce raisonnement, nous concluons que la proposition est fausse car la dimension de la somme des ensembles n'est pas égale à la dimension de R4.
Maths
Algèbre
MPSI/PCSI

Espaces supplémentaires (1)
Dans ce cours, nous abordons une question d'algèbre linéaire concernant deux droites vectorielles dans R3. La question est de savoir si ces deux droites sont supplémentaires. En d'autres termes, peut-on trouver deux ensembles, f et g, tels que tout vecteur de R3 puisse être décomposé de manière unique en un élément de f plus un élément de g. La dimension joue un rôle crucial dans la définition de supplémentaire. Dans le cas de deux droites vectorielles distinctes dans R3, qui ont chacune une dimension de 1, la somme des deux dimensions est égale à 2, ce qui est inférieur à la dimension de R3 qui est 3. Par conséquent, il n'est pas possible d'avoir des droites supplémentaires dans R3. En revanche, deux plans vectoriels distincts dans R3 ont chacun une dimension de 2, ce qui donne une somme des dimensions égale à 4, ce qui est supérieur à 3. Par conséquent, ces deux plans ne peuvent pas être supplémentaires l'un de l'autre. Pour qu'un plan vectoriel et une droite vectorielle dans R3 soient supplémentaires, la droite ne doit pas appartenir au plan. Dans le cas contraire, la dimension de l'espace reste à 2 au lieu de 3. En résumé, ces exemples illustrent différentes manières de découper l'espace et l'importance de la dimension dans la notion de supplémentarité.
Maths
Algèbre
MPSI/PCSI

Espaces supplémentaires (2)
Dans cet exercice, nous examinons quelques familles de vecteurs pour déterminer si elles sont supplémentaires dans R4. Nous avons 5 vecteurs : V1, V2, V3, V4 et V5. Pour former une base de R4, nous devons avoir au maximum 4 vecteurs. Nous commençons par vérifier si les vecteurs V1 et V2 sont supplémentaires. Pour cela, nous utilisons l'argument de dimension et constatons que la dimension de ces deux vecteurs combinés est de 3, ce qui ne correspond pas à une dimension de 4. Donc, ils ne sont pas supplémentaires. Ensuite, nous examinons les vecteurs V1 et V3. Si la famille V1, V2, V3, V4, V5 est libre, alors nous aurons des vecteurs supplémentaires. Nous résolvons un système pour vérifier si ces vecteurs sont linéairement indépendants et constatons qu'ils le sont, ce qui signifie qu'ils forment une base de R4. Donc, ils sont supplémentaires. Nous poursuivons ensuite avec les vecteurs V1, V3, V4 et V2, V5. Mais puisque V5 est égal à V3 + V4, l'intersection de ces deux ensembles n'est pas réduite à zéro, ce qui signifie qu'ils ne sont pas supplémentaires. Finalement, nous concluons que les vecteurs V1, V2, V4, V5 et V3, V4 ne sont pas supplémentaires.
Maths
Algèbre
MPSI/PCSI

Espaces supplémentaires
Dans ce cours sur les espaces vectoriels de dimensions infinies, on nous explique que bien que l'étude complète des dimensions infinies ne soit pas au programme, il est néanmoins important de savoir les gérer lorsqu'ils apparaissent. On nous présente l'exercice de montrer que l'ensemble des suites constantes et l'ensemble des suites convergentes vers 0 sont des sous-espaces supplémentaires dans E, l'ensemble des suites qui convergent. Pour cela, on nous propose une décomposition d'une suite en un élément qui converge vers 0 et un élément constant, et on doit montrer que cette décomposition est unique. En utilisant des raisonnements basiques et en se basant sur des conditions nécessaires et suffisantes, on parvient à trouver cette unique décomposition, prouvant ainsi que les ensembles des suites constantes et des suites convergentes vers 0 sont bien des sous-espaces supplémentaires dans E. On précise également qu'il est important de préciser que cette décomposition est la seule candidate possible, en vérifiant qu'elle satisfait bien les conditions nécessaires et suffisantes. On conclut en soulignant qu'il faut se familiariser avec ce type de raisonnement lorsqu'il n'y a pas de dimension finie, et en encourageant les questions et discussions sur le sujet.
Maths
Algèbre
MPSI/PCSI
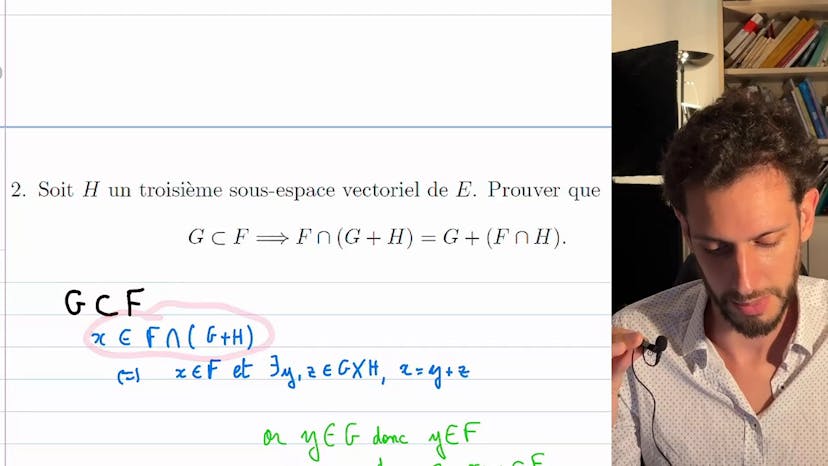
Sommes et union d’EV
Le cours explique comment démontrer qu'une intersection de deux sous-espaces vectoriels est un sous-espace vectoriel. Pour cela, l'auteur propose de considérer deux sous-espaces vectoriels f et g de l'espace vectoriel E. Il explique que si l'union de f et g est également un sous-espace vectoriel, alors soit f est inclus dans g, soit g est inclus dans f.
L'auteur utilise l'exemple géométrique de deux plans dans l'espace pour illustrer son raisonnement. Il montre que la somme de deux vecteurs, un provenant de chaque plan, ne peut pas appartenir à l'union des deux plans, à moins que l'un des plans ne soit inclus dans l'autre. Il conclut donc que la seule possibilité pour que l'union soit un sous-espace vectoriel est que l'un des plans soit inclus dans l'autre.
Il utilise ensuite des raisonnements basés sur les combinaisons linéaires pour démontrer le résultat. Il considère l'hypothèse que f union g est un sous-espace vectoriel et montre que si X appartient à f et Y appartient à g, alors X+Y doit appartenir à f union g. Il utilise alors les propriétés des sous-espaces vectoriels pour montrer que soit Y appartient à f si X+Y appartient à f, soit X appartient à g si X+Y appartient à g. Il conclut ainsi que si l'union est un sous-espace vectoriel, alors f est inclus dans g ou g est inclus dans f.
Dans la deuxième partie du cours, l'auteur aborde un exercice similaire avec un troisième sous-espace vectoriel H. Il montre comment utiliser les conditions nécessaires pour démontrer que l'intersection de deux sous-espaces vectoriels f et g plus H est égale à g plus l'intersection de f et H, sous l'hypothèse que g est inclus dans f. Il utilise des arguments basés sur les combinaisons linéaires pour montrer que si un élément X appartient à f et à g plus H, alors il appartient également à g plus l'intersection de f et H. Il conclut ainsi que si g est inclus dans f, alors l'intersection de f et g plus H est égale à g plus l'intersection de f et H.
En résumé, le cours démontre comment utiliser les conditions nécessaires et suffisantes pour prouver que l'union de deux sous-espaces vectoriels est un sous-espace vectoriel, et comment démontrer l'égalité entre l'intersection de deux sous-espaces vectoriels plus un troisième et la somme de ce troisième avec l'intersection de ces deux sous-espaces. L'auteur souligne l'importance de suivre un raisonnement précis et de travailler avec minutie pour résoudre ce genre d'exercices.
Maths
Algèbre
MPSI/PCSI

Fonctions paires et impaires
Ce cours porte sur les espaces vectoriels et les polynômes. L'objectif est de montrer que l'ensemble F des polynômes P tels que A divise P est un sous-espace vectoriel de R²x. Cette propriété est démontrée en utilisant les propriétés de la divisibilité des polynômes. Ensuite, l'exercice consiste à trouver un supplémentaire F pour cet ensemble. Pour cela, on utilise la division euclidienne des polynômes. On pose un polynôme A de degré N et on montre que tout élément de R²x peut être décomposé de manière unique en la somme d'un polynôme de F et d'un polynôme de degré inférieur à celui de A. Cette décomposition est possible grâce à l'unicité du quotient et du reste dans la division euclidienne. On conclut ainsi que F est bien un supplémentaire de F.
Maths Approfondies
Algèbre
ECG

Somme et intersections
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Espaces supplémentaires (1)
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Espaces supplémentaires (2)
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Espaces supplémentaires
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG
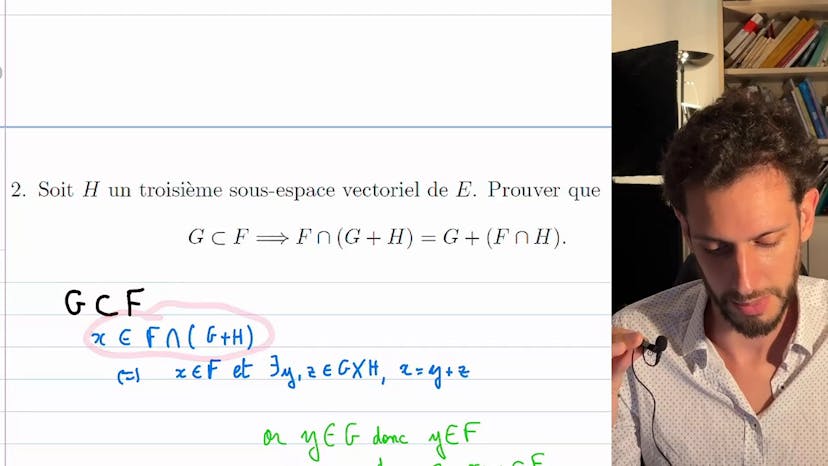
Sommes et union d’EV
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Fonctions paires et impaires
Aucun résumé n'est disponible pour cette vidéo


