 All subjects
All subjects
 All subjects
All subjects
Maths
Algèbre
MPSI/PCSI

Est-ce un EV ? Avec un SEV
Le cours concerne les espaces vectoriels et présente des techniques pour montrer si un espace est un espace vectoriel ou non. Il y a deux techniques principales :
1) Montrer que l'espace est un sous-espace vectoriel d'un espace vectoriel connu en vérifiant trois propriétés : l'inclusion dans un espace vectoriel, la conservation des éléments par combinaison linéaire et la présence de zéro dans l'espace.
2) Montrer que l'ensemble peut être écrit comme un VECT (ensemble des combinaisons linéaires) puisque tous les VECTS sont des espaces vectoriels.
Il est également possible d'utiliser la notion de noyau d'une application linéaire pour montrer qu'un espace est un espace vectoriel.
Le cours présente plus en détail la technique 1 pour un exemple spécifique où l'ensemble E1 est l'ensemble des vecteurs de R3 dont les coordonnées vérifient une équation donnée. Les trois critères sont vérifiés pour montrer que E1 est un sous-espace vectoriel de R3.
Maths
Algèbre
MPSI/PCSI
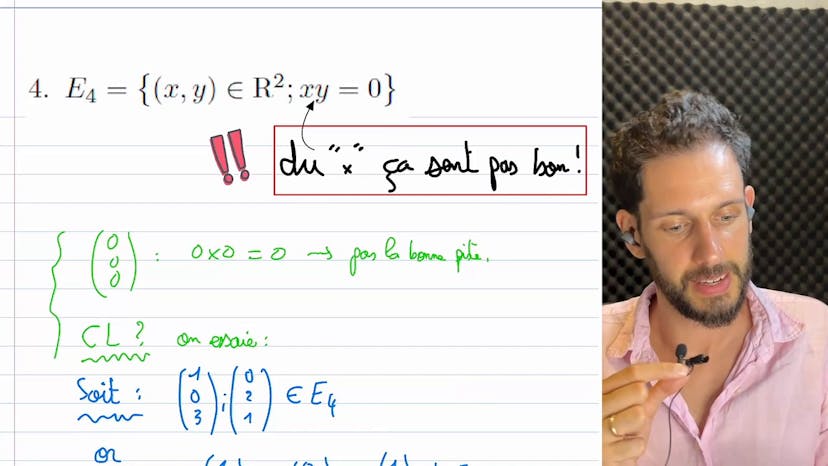
Cas où ce n'est PAS un EV
Dans cet extrait, le cours fait référence à différents cas où l'espace n'est pas un espace vectoriel. Le premier cas étudié est celui de E2, où l'équation x + y + 3z = 2 est donnée. Il est souligné que cette équation a une constante séparée des variables, ce qui indique un caractère non linéaire. En utilisant les définitions de base d'un espace vectoriel, il est prouvé que E2 n'est pas un espace vectoriel car l'élément 0 n'appartient pas à l'espace.
Les cas 4 et 5 sont également présentés comme des exemples où l'espace n'est pas un espace vectoriel. Il est mentionné que la technique habituelle de montrer que 0 n'appartient pas à l'espace ne fonctionne pas pour ces cas. Au lieu de cela, il est suggéré de trouver deux éléments dans l'espace tels que le produit de leurs coordonnées soit égal à 0. Ensuite, il est spécifié que si E4 est un espace vectoriel, la somme de ces deux éléments devrait également être dans E4. En prenant l'exemple de 1, 0 et 0, 2, il est montré que leur somme, 1, 2, n'est pas dans E4, ce qui prouve que E4 n'est pas un espace vectoriel.
Le dernier exemple présenté s'appelle E5 et montre également une relation non linéaire. Il est souligné que dès qu'il y a des constantes ou des relations non linéaires, cela peut indiquer que l'espace n'est pas un espace vectoriel. En prenant l'exemple de Y = X^2, il est prouvé que E5 n'est pas un espace vectoriel en montrant que la somme de deux éléments dans E5 n'est pas dans E5.
En résumé, le cours discute de ces différents cas pour illustrer des situations où l'espace n'est pas un espace vectoriel en utilisant des outils tels que l'élément 0 n'appartenant pas à l'espace, l'absence de conservation par combinaison linéaire, et l'existence de relations non linéaires ou de constantes.
Maths
Algèbre
MPSI/PCSI

C'est un Vect() donc un EV !
Le cours porte sur la démonstration qu'un espace est un espace vectoriel. Deux techniques sont présentées. La première consiste à prouver que l'espace est un sous-espace vectoriel en vérifiant trois conditions : l'inclusion dans un espace vectoriel, la conservation des combinaisons linéaires et la présence de l'élément nul. La deuxième technique consiste à montrer que l'espace peut s'écrire comme un espace de type vect, c'est-à-dire une combinaison linéaire de deux vecteurs u et v. Cette démonstration est appliquée à l'exemple de l'espace E3 qui est un sous-espace de R4. Les conditions d'appartenance à E3 sont traduites en termes de coordonnées et l'espace E3 est finalement prouvé être égal à vecte 2, 4, 4, 2, 1, ce qui en fait un espace vectoriel. Cette démonstration est rapide et nécessite de savoir bien traduire les conditions d'appartenance en termes de combinaisons linéaires. Il est important de maîtriser ce type de raisonnement en SEO friendly.
Maths
Algèbre
MPSI/PCSI

Union et intersection d'EVs
Dans ce cours, nous avons étudié différentes techniques pour déterminer si des ensembles sont des espaces vectoriels. Nous avons notamment examiné des exemples où les ensembles étaient définis par l'intersection ou l'union de deux ensembles.
Dans le cas d'une intersection, nous avons pris l'exemple de deux plans. Lorsque les plans sont distincts et non parallèles, leur intersection est une droite. Cette droite, passant par le point 0, peut être considérée comme un espace vectoriel de dimension 1.
En revanche, dans le cas d'une union, nous avons souligné la difficulté de prouver la conservation par combinaison linéaire. Nous avons pris l'exemple de deux plans, où il est possible de trouver des éléments dont la somme ne se trouve dans aucun des deux plans. Cela montre que l'union de ces deux ensembles n'est pas un espace vectoriel.
Pour démontrer ces résultats, nous avons utilisé une approche mathématique. Par exemple, pour le cas de l'intersection de deux plans, nous avons résolu un système d'équations pour obtenir une paramétrisation de la droite d'intersection.
Il est important de toujours se poser des questions et réfléchir à la situation avant de se lancer dans des calculs. Cette intuition initiale permet de mieux comprendre le problème et de choisir la bonne démonstration.
En conclusion, l'intersection de deux ensembles est souvent un espace vectoriel, tandis que l'union ne l'est généralement pas. Il faut cependant utiliser des méthodes mathématiques pour prouver ces résultats.
N'hésitez pas à poser vos questions en commentaire et restez attentifs pour nos prochaines vidéos.
Maths
Algèbre
MPSI/PCSI
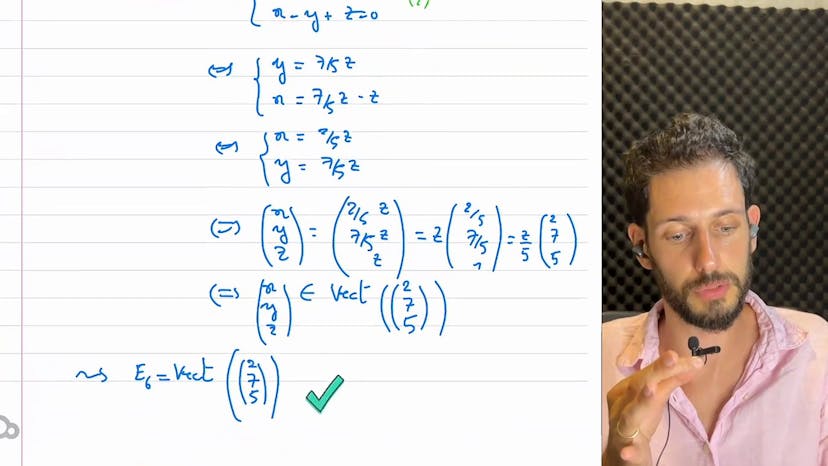
BONUS : utiliser le noyau
Dans cette transcription de vidéo, l'auteur explique comment montrer qu'un espace est un espace vectoriel en utilisant le noyau d'une application linéaire. Il explique que le noyau d'une application linéaire est similaire à la manière dont un espace peut être décrit comme un vecteur. Il montre ensuite comment utiliser cette méthode pour montrer que l'espace E1 est un espace vectoriel en utilisant une application linéaire spécifique. Il souligne que cette méthode est souvent utilisée dans les concours et est la façon la plus rapide de montrer qu'un espace est un espace vectoriel. Il conclut en disant que connaître cette technique est important dans les concours de haut niveau et que cela n'implique pas de vérifier toutes les propriétés de l'espace vectoriel.
Maths
Algèbre
MPSI/PCSI

Combinasion Linéaire
Dans cette vidéo, il est expliqué l'importance des combinaisons linéaires dans le domaine des espaces vectoriels. Différents exemples sont donnés où l'on demande si un vecteur peut être exprimé comme une combinaison linéaire d'autres vecteurs. Pour résoudre cela, on utilise des coefficients de combinaisons linéaires et on vérifie s'il existe une solution au système correspondant. On explique également qu'il est parfois plus simple de résoudre mentalement certains cas, mais dans d'autres cas, il est nécessaire de faire les calculs de manière plus détaillée. Un petit bonus est mentionné sur l'utilisation de deux vecteurs non parallèles comme base dans un plan. Dans le premier exemple, on démontre que le vecteur (1,2) peut être exprimé comme une combinaison linéaire des vecteurs u1 et u2. Dans le deuxième exemple, on démontre que le vecteur (-1/7,4/7) peut également être exprimé comme une combinaison linéaire des vecteurs u1, u2 et u3. Dans le troisième exemple, on résout un système de trois équations pour trouver les valeurs des coefficients de combinaisons linéaires, et on montre que le vecteur (2,4) ne peut pas être exprimé comme une combinaison linéaire des deux premiers vecteurs. Dans le quatrième exemple, on montre que la possibilité d'exprimer le vecteur (2,4) comme une combinaison linéaire des deux premiers vecteurs dépend de la valeur de m. On conclut en soulignant l'importance de savoir utiliser les combinaisons linéaires et en encourageant les questions des spectateurs.
Maths
Algèbre
MPSI/PCSI

Sous-espace engendré
Dans cet exercice, nous devons trouver des valeurs réelles pour que certains vecteurs appartiennent à un ensemble F, qui est le sous-espace vectoriel engendré par deux vecteurs. Ce sous-espace est en réalité un plan de taille 2, formé par toutes les combinaisons linéaires de ces deux vecteurs.
Pour résoudre ce problème, nous posons un système d'équations où nous cherchons à déterminer les constantes alpha et bêta, qui permettront de créer des combinaisons linéaires pour que le vecteur lambda mu-37-3 appartienne à F. Cependant, les calculs peuvent devenir compliqués en raison de la présence du terme -37.
Nous utilisons les deux premières lignes du système comme contraintes pour trouver les valeurs uniques de lambda et mu, une fois que nous avons trouvé alpha et bêta. Les deux dernières lignes du système sont deux équations qui nous permettent de déterminer les valeurs de alpha et bêta.
En résolvant le système, nous trouvons les valeurs de bêta (moins 126 sur 47) et d'alpha (247 sur 47). Bien que ces valeurs puissent sembler compliquées, elles nous permettent d'obtenir les seules valeurs possibles de lambda et mu pour que le vecteur soit inclus dans F.
Les valeurs trouvées pour lambda et mu sont respectivement moins 5 sur 47 et une expression complexe. L'astuce de cet exercice est de ne pas paniquer face à la présence de lambda et mu, mais plutôt de suivre la même démarche en introduisant alpha et bêta pour obtenir une combinaison linéaire et ensuite analyser les conditions qui déterminent les valeurs de lambda et mu.
Cet exercice sert à clarifier les détails de la résolution de problèmes similaires et à vérifier si vous maîtrisez bien les étapes nécessaires. Il est important de ne pas paniquer et de prendre la liberté de poser des éléments supplémentaires pour résoudre le problème.
J'espère que ce résumé vous a aidé et je vous retrouve dans une prochaine vidéo. Au revoir !
Maths
Algèbre
MPSI/PCSI

Famille libre
Ce cours traite de la notion de liberté ou de liaison d'une famille de vecteurs. L'objectif est de déterminer si une famille donnée est libre ou liée en utilisant une méthode classique. On suppose l'existence d'une combinaison linéaire qui lie tous les éléments de la famille ensemble, et on cherche à trouver une contradiction à cette hypothèse. Si une telle combinaison linéaire existe, alors tous les coefficients doivent nécessairement être égaux à zéro, ce qui prouve que la famille est libre.
On écrit donc cette combinaison linéaire et on la traduit en un système d'équations, qu'on résout pour trouver les coefficients lambda et mu. Si on trouve que tous les coefficients sont nuls, cela signifie que la famille est libre. On répète cette démarche pour différentes paires de vecteurs de la famille pour déterminer si elles sont libres ou liées.
Enfin, pour déterminer si la famille de vecteurs dans son ensemble est libre ou liée, on rédige une nouvelle combinaison linéaire en introduisant des coefficients lambda1, lambda2, et lambda3, et on cherche à trouver si cette combinaison linéaire a une solution unique. Si elle en a, alors la famille est liée, sinon elle est libre.
Dans l'exemple donné, on observe que la famille v1, v2, v3 est liée, car il est possible de trouver une combinaison linéaire telle que -2v1 + v2 - v3 = 0, ce qui montre que les trois vecteurs sont liés dans un plan et qu'aucun d'entre eux ne sort de ce plan. Cela signifie que la famille ne couvre pas l'ensemble de l'espace, ce qui fait qu'elle est liée.
Maths
Algèbre
MPSI/PCSI

Famille liée
Le cours traite des familles libres et de leur complexité croissante dans les exercices proposés. Le thème de l'exercice est l'espace vectoriel et les suites réelles. Trois suites différentes sont considérées : la suite des cosinus nθ, la suite cosinus nθ plus a, et la suite cosinus nθ plus b. Le but est de déterminer si la famille est liée.
L'approche utilisée est d'appliquer la formule trigo cos(a + b) = cos(a) cos(b) - sin(a) sin(b) aux deux suites complexes. En utilisant cette formule, on peut réécrire les deux suites en termes de cos(nθ) et quelques coefficients réels. Cependant, il reste un terme contenant sin(nθ) qui dépend de n et rend la famille difficile à combiner.
Pour éliminer ce terme, l'idée est d'utiliser une combinaison des suites en multipliant la première par sin(b) et la deuxième par sin(a), puis en soustrayant les deux résultats. Cela permet d'obtenir une expression ne contenant plus le terme problématique. En reconnaissant une autre formule trigo, on peut écrire une combinaison linéaire des éléments de la famille : cos(nθ) = cos(a) sin(b) - cos(b) sin(a).
Cette combinaison linéaire prouve que la famille est liée. L'exercice illustre ainsi la complexité croissante des tests de liberté et la nécessité de développer des compétences pour les résoudre. Le professeur conclut en invitant les étudiants à poser des questions et en promettant une prochaine vidéo.
Maths
Algèbre
MPSI/PCSI
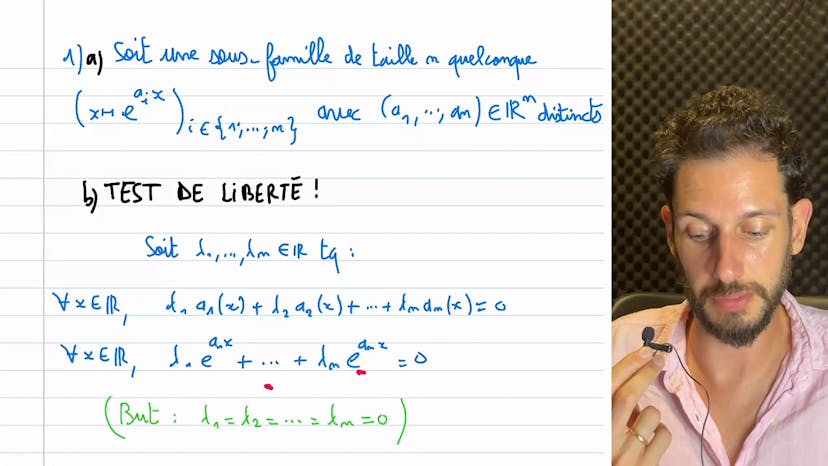
Liberté et familles de fonctions
Aucun résumé n'est disponible pour cette vidéo
Maths
Algèbre
MPSI/PCSI
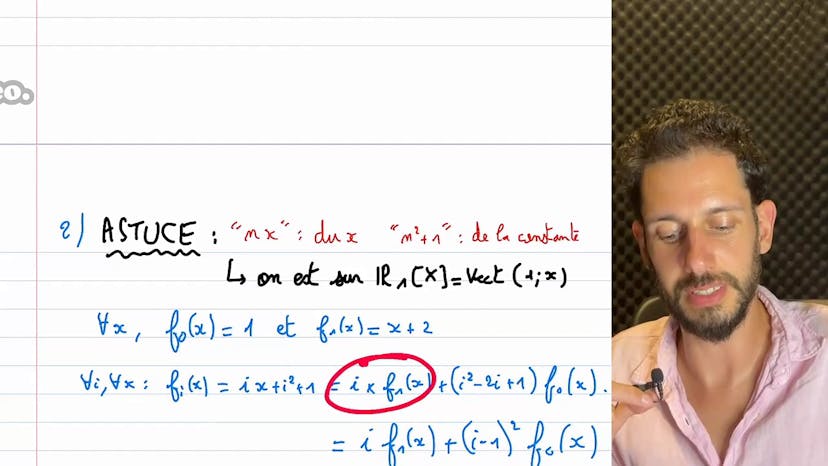
Encore des familles de fonctions
Le cours porte sur la question de savoir si une famille de fonctions est libre ou non. Dans la question 1, on nous donne trois fonctions sinus différentes et on nous demande de montrer si elles sont liées. Tout d'abord, on utilise quelques formules trigonométriques pour exprimer ces fonctions uniquement en fonction de sinus. Ensuite, on montre que deux des fonctions sont liées à sinus x et on fait la même démarche avec la troisième fonction pour obtenir une relation entre les trois fonctions. Ainsi, on conclut que la famille est liée.
Dans la question 2, on nous donne une famille de fonctions qui sont des polynômes de degré 1. Au début, l'auteur se perd un peu dans ses calculs, mais réalise finalement que toutes ces fonctions sont en fait des combinaisons linéaires d'une constante et de x. Donc, quel que soit l'élément de la famille, on peut l'exprimer comme une combinaison linéaire des deux premiers éléments de la famille. Donc, toute sous-famille de cette famille est également liée, ce qui signifie que la famille entière est liée.
En conclusion, le cours traite de la question de la liberté d'une famille de fonctions. Dans les deux questions abordées, on montre que les familles sont liées, ce qui signifie qu'elles ne sont pas libres. L'auteur souligne également l'importance de prendre du recul et de comprendre les structures mathématiques pour résoudre efficacement ce type d'exercice.
Maths
Algèbre
MPSI/PCSI

Famille recomposée
Résumé SEO-friendly :
Ce cours présente un exercice visant à déterminer si une famille de vecteurs est libre. La famille est construite à partir d'éléments précédents en utilisant des combinaisons linéaires. On pose des réels λ1, λN et on réécrit les équations en fonction de ces coefficients. On cherche à exprimer les coefficients en fonction de λN pour déterminer si la famille est libre. Cependant, l'exercice se complique car il faut tenir compte de la parité des indices. Pour faciliter les calculs, l'enseignant recommande d'utiliser des points de suspension plutôt que des sommes. Finalement, il démontre que si le nombre d'éléments dans la famille est pair, alors la famille est liée, tandis que si le nombre d'éléments est impair, alors la famille est libre. Il souligne l'importance de rester concentré et organisé lors de la résolution d'exercices de ce type.


