 All subjects
All subjects
 All subjects
All subjects
Maths
Analyse
MPSI/PCSI

Continuité en un point
Dans cette vidéo, Paul traite de la continuité de la fonction g sur R. La fonction g est définie comme étant égale à 1 sur l'hégaryme de valeur absolue de x si x n'est pas égale à moins 1, 0 ou 1, et 0 si x est égale à moins 1, 0 ou 1. La question posée est de savoir en quels points g est continue. Dans un premier temps, Paul traite le cas où x appartient à R privé de moins 1, 0 ou 1, et il montre que g est continue sur cette partie de R. Il étudie ensuite la continuité de g en moins 1, 0 et 1. Il montre que g est continue en 0, mais pas en 1 et moins 1. Par conséquent, la fonction g est continue sur R privé de moins 1 et 1.
Maths
Analyse
MPSI/PCSI

Continuité avec paramètres
Dans cette vidéo, on explore la continuité de fonctions et on étudie pour quelle valeur de a la fonction f est continue, ainsi que pour quelle valeur alpha, beta et gamma les fonctions g sont continues. On vérifie également que les morceaux de fonctions sont bien raccordés entre eux, et pour quelles valeurs de constantes. La fonction f est continue sur r privé de 1 pour a=1 ou 0, et g est continue sur r privé de 0 et 1 pour alpha, beta et gamma appartenant à l'ensemble x 1 moins x, x pour x appartenant à R.
Maths
Analyse
MPSI/PCSI

Prolongements par continuité de fonctions cosinus et sinus
Dans cette vidéo, Paul étudie le prolongement par continuité de fonctions contenant des sinus et des cosinus. Il commence par examiner si la fonction f2x = sinx*sin(1/x) est prolongeable par continuité à R entier. En appliquant une inégalité et en montrant que la limite en 0 est bornée, il conclut que la fonction est bien prolongeable par continuité. En revanche, lorsqu'il examine la fonction g = cos(x)*cos(1/x), il constate que cette fonction ne peut être prolongeable par continuité car cos(1/x) tend vers 1 en 0, ce qui ne permet pas d'écraser les oscillations. Paul utilise la méthode de considération de deux suites qui tendent vers 0 mais dont les limites diffèrent, pour prouver que la limite de g en 0 n'existe pas. Enfin, Paul étudie la fonction h = sin(x+1)*ln(1+x) qui présente une forme indéterminée en -1. En appliquant une astuce pour ramener la limite en 0, il montre que la fonction est prolongeable par continuité. Ainsi, il conclut que h est bien prolongeable par continuité sur R.
Maths
Analyse
MPSI/PCSI
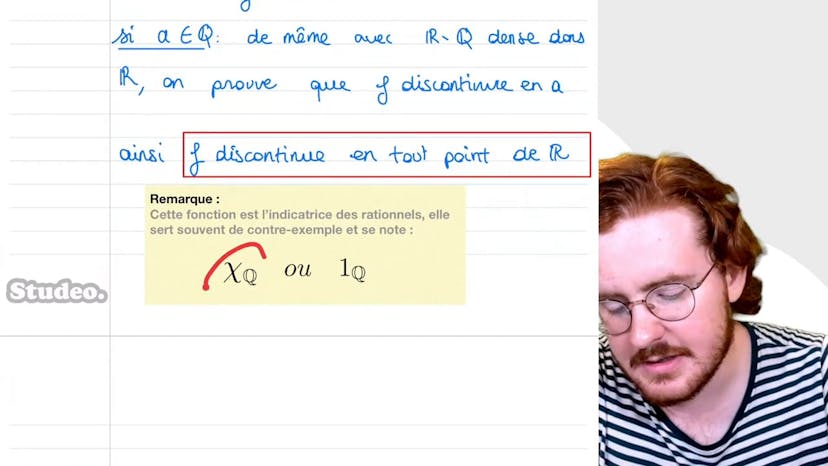
Indicatrice de Q
La fonction f de r dans R est définie par 1 si x est rationnel et 0 si x n'est pas rationnel. Il est montré que f est discontinue en tout point en utilisant la caractérisation séquentielle de la continuité. On prend un point a dans R et on montre qu'il existe une suite de réels qui tend vers a et dont la limite de f de ces réels n'est pas égale à f de a. Si a est irrationnel, on utilise le fait que R privé de q est dense dans R pour montrer la discontinuité. Cette fonction, l'indicatrice des irrationnels, est simple et sert souvent de contre-exemple sur la continuité.
Maths
Analyse
MPSI/PCSI
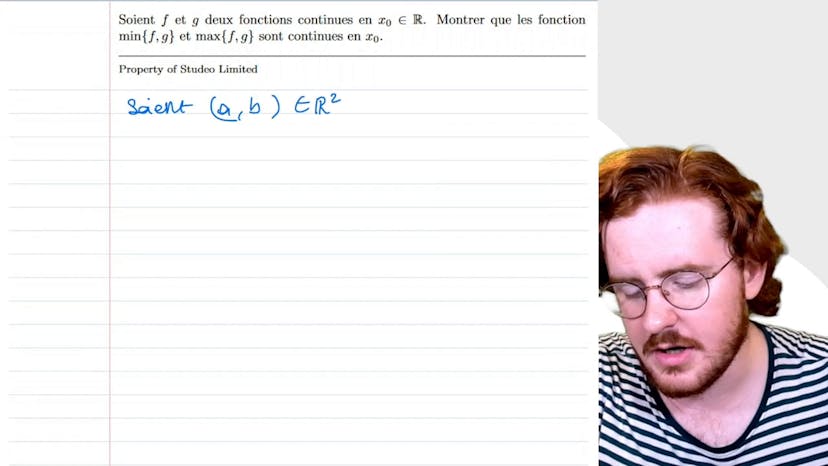
Fonctions min et max
Nous apprenons dans cette vidéo que les fonctions minimum et maximum de deux fonctions continues f et g en x0 sont elles-mêmes continues en x0. Pour prouver cela, il est plus efficace de se rappeler que les expressions du minimum et du maximum peuvent être écrites visuellement en fonction de f et g, plutôt que d'utiliser la définition de la continuité ou des suites. En utilisant des formules classiques, le maximum de a et b est donné par a + b + |a - b|/2 et le minimum de a et b par a + b - |a - b|/2. Les formules correspondantes pour les fonctions minimum et maximum de f et g en x0 sont alors 1/2(f+g+|f-g|) et 1/2(f+g-|f-g|). Étant donné que f et g sont continues en x0, la différence de f et g est continue en x0 et la valeur absolue de cette différence est également continue. Ainsi, par les théorèmes généraux, les fonctions minimum et maximum de f et g en x0 sont bien continues en x0.
Maths
Analyse
MPSI/PCSI

Équation fonctionnelle
Dans cette vidéo, Paul résout une équation fonctionnelle pour trouver les fonctions continues vérifiant que f(x+y) = f(x) + f(y). Il note que les fonctions linéaires (f(x) = ax) vérifient cette équation, et utilise la densité des rationnels pour prouver que toute fonction vérifiant cette équation est linéaire. Il prouve également que f(0) = 0 et que f(nx) = nf(x) pour tous les entiers n et x. Enfin, il montre que toute fonction vérifiant cette équation est bien une fonction linéaire.
Mathématiques
Analyse
ECG
Continuité en un point
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Continuité avec paramètres
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Prolongements par continuité de fonctions cosinus et sinus
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Indicatrice de Q
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Fonctions min et max
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Équation fonctionnelle
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Continuité en un point
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Continuité avec paramètres
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Prolongements par continuité de fonctions cosinus et sinus
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Indicatrice de Q
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Fonctions min et max
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Équation fonctionnelle
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Continuité en un point
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Continuité avec paramètres
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Prolongements par continuité de fonctions cosinus et sinus
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Indicatrice de Q
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Fonctions min et max
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Équation fonctionnelle
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Continuité en un point
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Continuité avec paramètres
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Prolongements par continuité de fonctions cosinus et sinus
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Indicatrice de Q
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Fonctions min et max
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Équation fonctionnelle
Aucun résumé n'est disponible pour cette vidéo


