 All subjects
All subjects
 All subjects
All subjects
Maths
Fonctions
Seconde

Définition d'un minimum
Dans cet exercice, nous apprenons à déterminer le minimum d'une fonction sur R. Pour ce faire, nous devons remarquer que la forme développée de f(x) est équivalente à sa forme canonique x-4²-13. Ensuite, il faut minorer f en trouvant le plus grand k tel que f(x) est supérieur ou égal à k. Nous savons que x-4² est positif, donc f(x) est supérieur ou égal à -13. Cependant, le plus grand des minorants est le minimum de f, qui est égal à -13 et atteint pour x égal à 4.
Maths
Fonctions
Seconde

Tableau de variations 1 : inéquation
L'exercice explique comment résoudre une inéquation f2x > k en utilisant un tableau de variation. Les valeurs de f2x qui sont plus grandes que k sont repérées et la solution de l'inéquation est l'ensemble des points d'abscisse correspondant à ces valeurs. Le tableau est complété avec les informations supplémentaires données pour aider à repérer les valeurs. La solution de l'inéquation est l'intervalle entre moins 7 et moins 1 exclus, ainsi que l'intervalle entre 9 exclus et l'infini si f de x est strictement plus grand que 2.
Maths
Fonctions
Seconde
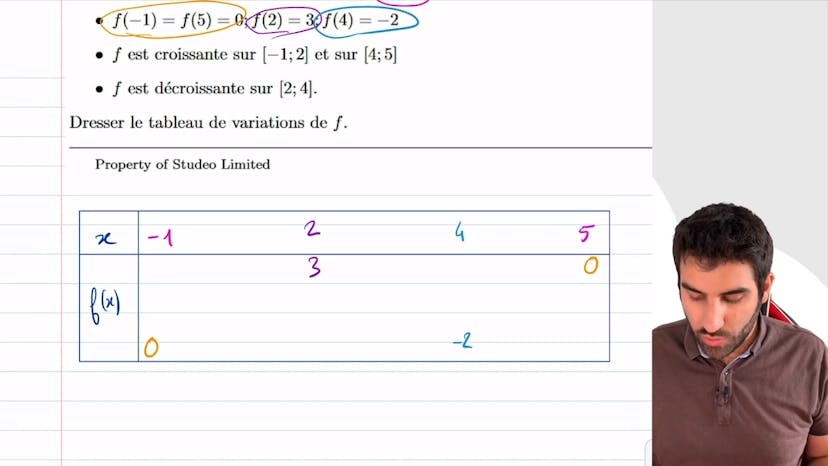
Tableau de variations 3 : tracé
Dans cet exercice, on apprend à dresser le tableau de variation d'une fonction en se basant sur plusieurs informations données. On commence par dessiner un tableau de variation standard qui a deux lignes et deux colonnes. La première ligne représente les valeurs de x, tandis que la deuxième ligne représente les valeurs de f (x) avec des flèches correspondantes aux variations. Ensuite, on remplit le tableau en utilisant les informations fournies. Si la fonction f est définie sur un intervalle donné, les bornes de cet intervalle seront les valeurs de x à gauche et à droite du tableau. On utilise ensuite les différentes informations pour remplir les cases du tableau. Les nombres sont mobiles et peuvent être déplacés en fonction des variations. Les flèches indiquent si la fonction est croissante ou décroissante sur l'intervalle donné. Une fois toutes les informations traitées, le tableau de variation de la fonction est complet.
Maths
Fonctions
Seconde

Tableau de variations 2 : comparaison
Dans cet exercice de mathématiques, on apprend à utiliser le tableau de variation d'une fonction pour comparer deux images de cette fonction. Les images de la fonction sont placées sur le tableau en fonction de leurs antécédents. En utilisant ces informations, on peut déterminer que f de "-4" est entre "-13" et "-6", et que f de 6 est entre 2 et 8. Grâce à la transitivité d'inéquation, on peut conclure que f de "-4" est plus petit que f de 6.
Maths
Fonctions
Seconde

Reconnaître des fonctions
Dans cet exercice, nous traduisons des informations sur des fonctions en écriture explicite. La première fonction est affine avec une écriture de 3x-2. La deuxième fonction affine est de 2x-2 plus 6. La troisième fonction est une fonction carrée avec une écriture de x². La quatrième fonction est une fonction inverse avec une écriture de 1 sur x. Connaissant le fait que les fonctions affines passent par zéro et la fonction carrée s'annule également en zéro, la fonction inverse n'a pas d'antécédent par cas et n'est pas définie en zéro. La fonction carrée est la seule fonction restante qui peut avoir plusieurs antécédents. La fonction g est croissante sur son ensemble de définitions, ce qui signifie que la fonction g est 3x-2 et la fonction h est -2x plus 6.
Maths
Fonctions
Seconde

Comparaison de racines
Dans ce cours, on apprend comment comparer deux nombres donnés sous forme de fractions avec des racines carrées. On utilise des inégalités successives en commençant par le plus petit noyau, puis en appliquant des fonctions croissantes ou décroissantes comme la racine carrée ou la fonction inverse. On rappelle que la racine carrée est croissante sur les nombres positifs et que la fonction inverse est décroissante sur les nombres positifs. Finalement, on peut obtenir une inégalité entre les deux nombres à comparer en appliquant ces méthodes avec des exemples concrets. On obtient donc que 2 sur 3 plus racine de 5 est strictement plus grand que 2 sur 3 plus racine de 7.


