 All subjects
All subjects
 All subjects
All subjects
Maths SM&SP
Algèbre
2BAC SM Maroc
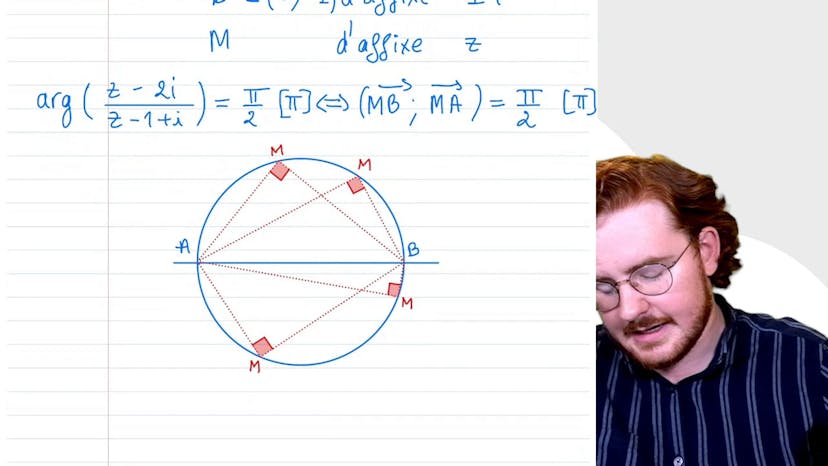
Lieu géométrique avec l’argument
Dans cette vidéo, Paul explore les relations entre des équations avec des complexes et des objets géométriques. Dans la première question, il cherche à déterminer l'ensemble des points M dont l'affixe Z vérifie la relation complexe Z-2 = rho * i, avec rho appartenant à R+. En termes géométriques, cela signifie que les points M se trouvent sur une demi-droite partant de l'origine et tournant de pi/2, décalée vers la droite de 2.
Dans la deuxième question, la relation est l'argument de Z / (1 + i) = pi/2 mod 2pi. En utilisant la forme exponentielle du nombre complexe 1 + i, Paul trouve que les points M sont situés sur une demi-droite partant de l'origine et passant par le point (-1, 1).
Dans la troisième question, Paul cherche les points M tels que l'argument de (Z-2i) / (Z-1+i) = pi/2 mod pi. Il introduit les points A (0,2) et B (1,1) qui permettent d'écrire l'argument en termes d'angles entre les vecteurs MB et MA. Finalement, il conclut que l'ensemble des points M forme un cercle dont le rayon est le segment AB.
C'est ainsi que Paul résume le contenu de cette vidéo orientée vers les relations entre équations complexes et objets géométriques.
Maths SM&SP
Algèbre
2BAC SM Maroc

Lieu géométrique avec le module
Dans cette vidéo, Paul explique comment déterminer le lieu géométrique des points M dont la fixe Z vérifie certaines relations sur le module. Il commence par assimiler le plan complexe au repère OUV. Ensuite, il pose Z comme étant égal à A + IB pour simplifier les calculs. Il réécrit l'équation de la relation module et utilise les carrés des modules pour faciliter les calculs. Finalement, il détermine que les points M recherchés appartiennent à la droite des réelles, c'est-à-dire la droite des abscisses sur le plan OUV. Pour la deuxième question, il utilise la même méthode et détermine que les points M recherchés sont également sur la droite des réelles. Ainsi, l'ensemble des points M pour les deux questions est la même, c'est la droite des réelles.
Maths SM&SP
Algèbre
2BAC SM Maroc

Transformations du plan
Dans cet exercice, nous abordons les transformations géométriques du plan complexe. Nous devons déterminer la nature des éléments caractéristiques de ces transformations.
La première question concerne une rotation de centre haut et d'angle -π/2, représentée par l'écriture complexe z → 1/(iz).
La deuxième question concerne une translation du vecteur d'affix i, représentée par l'écriture complexe z → z + 2i.
La troisième question concerne une similitude de centre (1,1), rapport 2 et angle π/3, représentée par l'écriture complexe z → (1 + i√3)z.
La quatrième question concerne une similitude d'angle α et de centre (1,0), représentée par l'écriture complexe z → (1 + i tanα)z - i tanα.
La réponse à chaque question est résumée de manière claire et concise, en utilisant des termes SEO-friendly.
Maths SM&SP
Algèbre
2BAC SM Maroc

Lieux géométriques
Dans cette vidéo, Paul aborde un exercice sur les nombres complexes et leur interprétation géométrique. L'exercice consiste à déterminer le lieu géométrique des points M dont l'affixe Z satisfait une certaine condition. Paul explique que pour avoir trois points alignés, l'argument de la différence des affixes de ces points doit être égal à 0 modulo pi. Il précise également que si au moins deux points sont égaux, alors ils sont automatiquement alignés. Ensuite, il considère une condition sur la partie réelle de Z-1 divisée par Z-I, et il la traduit en termes d'arguments complexes. Il en déduit que le triangle formé par les points 1, I et Z est rectangle, quel que soit Z appartenant au cercle de centre racine de 2 et de diamètre 1. Pour la deuxième question, Paul montre que les points vérifiant la condition de la partie réelle de Z-1 divisée par Z-I égale à 0 appartiennent également au même cercle. Enfin, pour la troisième question sur un triangle rectangle formé par les points M, P et Q, Paul rappelle qu'ils doivent être distincts pour former un triangle. Il explique comment traduire cette condition en termes d'arguments complexes et montre que les points M correspondants forment une droite d'équation X égale à moins 1. Puis il détermine les droites correspondantes aux points P et Q, qui sont l'axe des imaginaires purs et une droite parallèle à l'axe des réels passant par le point (-1, 0). Enfin, Paul conclut l'exercice en récapitulant les résultats obtenus pour chaque condition et en soulignant que les points M forment un cercle de centre (-1, 0) et de rayon 1,5.
Maths SM&SP
Algèbre
2BAC SM Maroc

Théorème de Napoléon
Dans cette vidéo, Paul nous présente un exercice sur les complexes et l'interprétation géométrique des complexes. Il commence par poser les idées de l'exercice, où le plan Euclidien est utilisé avec le repère O E1 E2. Il utilise la notation J pour désigner E I 2pi sur 3, qui représente les racines 3ème de l'unité.
L'objectif de l'exercice est de montrer que le triangle U V W est équilatéral direct si et seulement si U moins V est égal à moins J carré W moins V. Paul explique qu'il va d'abord prouver le sens direct puis le sens réciproque de cette équivalence, car cela simplifie les calculs.
Il explique également que les racines 3ème de l'unité forment un triangle équilatéral, ce qui pourrait être utile pour résoudre l'exercice. Il remarque que l'égalité U moins V égal à moins J carré W moins V ressemble à une rotation, où U est l'image de W par une rotation d'un certain angle. Il utilise ensuite cette observation pour prouver le sens réciproque de l'équivalence.
Pour la deuxième question, il souhaite montrer que le triangle U V W est équilatéral direct si et seulement si U plus IV plus I carré omega est égal à 0. Il note que cette égalité ressemble à l'égalité précédente, donc il souhaite prouver que cette égalité est équivalente à l'autre. En utilisant la transitivité de l'équivalence et les résultats de la première question, il démontre cette équivalence.
Pour la troisième question, qui concerne une construction géométrique complexe, Paul explique qu'il est nécessaire de faire des dessins pour bien comprendre. Il évoque le centre de gravité d'un triangle équilatéral, qui est l'intersection des médianes, des hauteurs ou des bissectrices. Il utilise les résultats des deux premières questions pour résoudre cette question et montre que les centres de gravité du triangle U V W et du triangle A B C sont concordants.
En conclusion, Paul résume les différentes étapes de l'exercice et rappelle que le dessin ne constitue pas une preuve, mais peut aider à l'illustrer. Il termine en disant au revoir et en nous invitant à la prochaine vidéo.
Maths SM&SP
Algèbre
2BAC SM Maroc
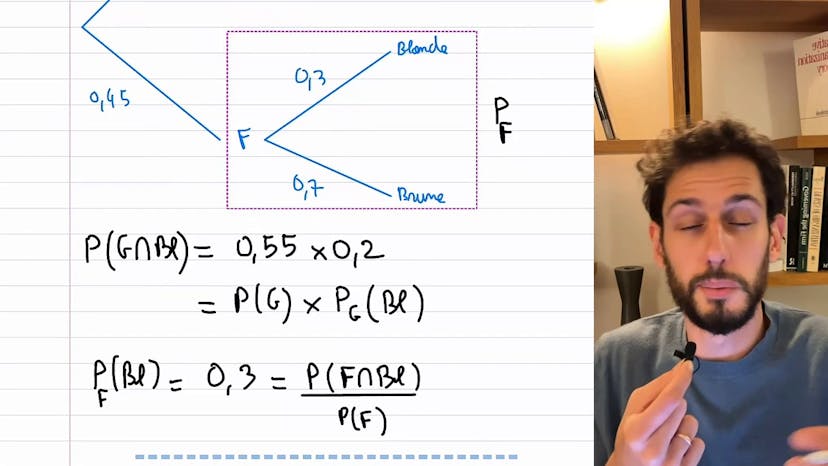
Les probabilités conditionnelles
Lors de l'introduction des probabilités, il est souvent plus facile de commencer par un exemple concret plutôt que des formules théoriques. Dans cet exemple, nous considérerons un lycée où il y a 55% de garçons et 45% de filles. Parmi les garçons, 20% sont blonds et 80% sont bruns. Parmi les filles, 30% sont blondes et 70% sont brunes. Nous pouvons définir les probabilités conditionnelles, qui sont les probabilités dans un sous-univers. Par exemple, la probabilité d'être blond est de 20% pour les garçons et de 30% pour les filles. Chaque probabilité conditionnelle est définie en fonction du sous-univers dans lequel nous nous trouvons.
Nous pouvons également calculer la probabilité d'un événement donné en combinant différentes probabilités conditionnelles. Par exemple, la probabilité d'être un garçon blond est de 0,55 (probabilité d'être un garçon) multipliée par 0,2 (probabilité d'être blond parmi les garçons). De même, la probabilité d'être une fille blonde est de 0,45 (probabilité d'être une fille) multipliée par 0,3 (probabilité d'être blond parmi les filles).
Nous pouvons aussi exprimer la probabilité d'un événement dans un sous-univers en utilisant la probabilité totale et la probabilité de l'événement dans cet univers. Par exemple, la probabilité d'être blonde parmi les filles est la probabilité d'être une fille blonde divisée par la probabilité d'être une fille.
La formule générale pour les probabilités conditionnelles est la probabilité de l'événement B sachant l'événement A, divisée par la probabilité de l'événement A. Cette formule peut être appliquée à n'importe quel événement A et B.
Maths SM&SP
Algèbre
2BAC SM Maroc
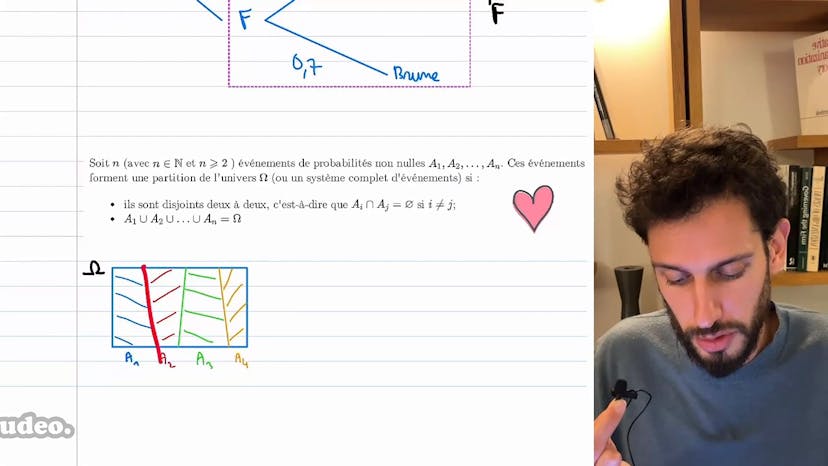
Partition de l'univers
La notion de partition de l'univers est importante en probabilités. Une partition de l'univers consiste à diviser les événements possibles en sous-événements qui n'ont rien en commun. Par exemple, on peut considérer l'univers des garçons comme un sous-univers, et les événements possibles dans ce sous-univers peuvent être les garçons blonds ou les garçons bruns. Une partition est une division de l'univers qui doit satisfaire deux conditions : tous les événements possibles doivent être couverts et il ne doit pas y avoir d'intersection entre les sous-événements. Par exemple, dans l'univers des garçons, on peut diviser en garçons blonds et garçons bruns, mais il ne peut y avoir aucune intersection entre ces deux groupes. On peut également réaliser une partition entre garçons et filles au niveau du lycée. En termes de probabilités, une partition est un ensemble d'événements disjoints qui couvrent tout l'univers. Une partition peut être représentée par des événements a1, a2, ..., an, avec des probabilités associées. Il est important que les événements soient disjoints, c'est-à-dire qu'ils n'aient rien en commun, et que leur union forme tout l'univers.
Maths SM&SP
Algèbre
2BAC SM Maroc
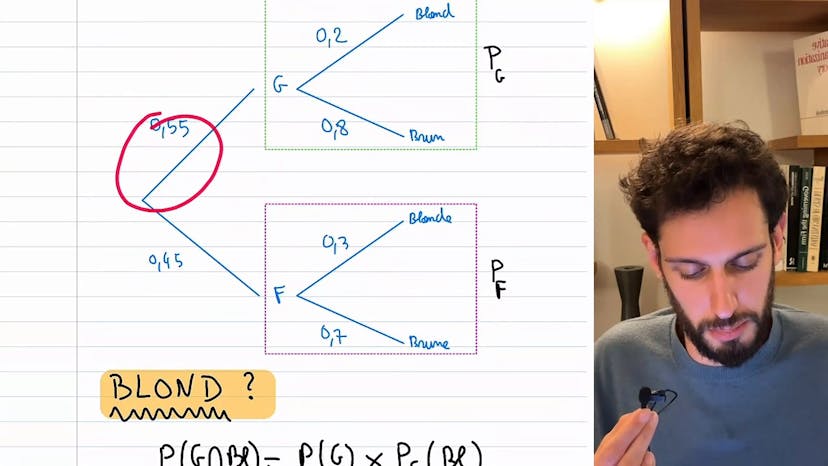
La formule des probas totales
La formule des probabilités totales est une formule très importante que l'on peut appliquer pour calculer des probabilités dans un contexte donné. Dans cet exemple, nous prenons le lycée comme univers et nous créons une partition entre garçons et filles, ainsi qu'entre les différentes couleurs de cheveux. Nous avons utilisé la formule des probabilités conditionnelles pour calculer la probabilité d'être à la fois blond et garçon, en multipliant la probabilité d'être garçon par la probabilité d'être blond parmi les garçons. Maintenant, nous pouvons nous intéresser à une probabilité plus globale, celle d'avoir les cheveux blonds. Imaginons un lycée avec 100 personnes, 55 garçons et 45 filles. Nous voulons savoir quelle est la probabilité, en tirant une personne au hasard, de tomber sur quelqu'un qui a les cheveux blonds, qu'il soit garçon ou fille. L'idée est de ne pas se focaliser uniquement sur les personnes blondes, mais de prendre en compte les deux catégories. Il y a deux chemins possibles pour tirer une personne blonde : soit on tire un garçon blond, soit on tire une fille blonde. La formule des probabilités totales consiste à sommer les probabilités de ces deux événements pour obtenir la probabilité d'être blond. En d'autres termes, la probabilité d'être blond est égale à la probabilité d'être un garçon blond plus la probabilité d'être une fille blonde. On peut aussi écrire cela en utilisant la formule des probabilités conditionnelles. Cette formule nous permet de parcourir toutes les branches de l'arbre des événements et de les sommer pour obtenir la probabilité recherchée. En théorie, si nous avons une partition de l'univers, la probabilité d'un événement B est égale à la somme des probabilités de B dans chaque branche de la partition. Cette formule peut être utilisée en remplaçant chaque probabilité par la formule des probabilités conditionnelles correspondante. Il est important de comprendre intuitivement le sens de cette formule : nous cherchons l'événement dans chaque branche et les sommons toutes. J'espère que cela était clair. N'hésitez pas à laisser des commentaires si nécessaire. À bientôt dans une prochaine vidéo !
Maths SM&SP
Algèbre
2BAC SM Maroc

Indépendance
L'indépendance, une notion très importante en probabilité, peut être expliquée de manière claire en utilisant des exemples. Dans cet exemple, nous avons deux variables : le sexe (garçon ou fille) et la couleur des cheveux (blond ou brun). Nous avons également des probabilités associées à chaque événement. Par exemple, la probabilité d'être blond en étant garçon est de 0,2, et la probabilité d'être blond en étant fille est de 0,3.
Pour déterminer la probabilité d'être blond dans ce lycée, nous utilisons la formule des probabilités totales. Cependant, il est important de noter que la couleur des cheveux dépend du sexe. Par conséquent, la probabilité d'être blond dépend de si vous êtes un garçon ou une fille. Ces événements sont donc dépendants.
Cependant, il est également possible d'avoir des événements indépendants. Par exemple, si la probabilité d'être blond est la même pour les garçons et les filles, il s'agit d'un événement indépendant. Dans ce cas, peu importe si vous êtes un garçon ou une fille, la probabilité d'être blond est de 30%.
Il est important de comprendre les définitions formelles en mathématiques, mais il est également utile de les considérer avec des exemples concrets. Les formalités théoriques viennent ensuite pour renforcer la compréhension. Il est également intéressant de noter que si deux événements A et B sont indépendants, leurs complémentaires (non A et non B) le sont également.
En résumé, l'indépendance en probabilité se réfère à des événements qui ne dépendent pas les uns des autres. Dans le cas de l'exemple, si la probabilité d'être blond ne dépend pas du sexe, alors ces événements sont indépendants.
Maths SM&SP
Algèbre
2BAC SM Maroc
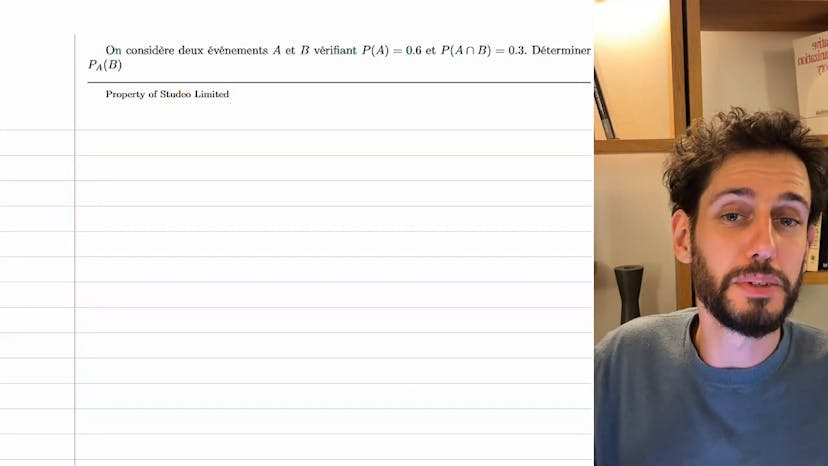
Application calculatoire
Dans ce cours, nous allons apprendre à appliquer la formule des probabilités conditionnelles. Tout d'abord, nous avons deux événements, A et B. Nous voulons trouver P2B sachant A, en utilisant la formule des probabilités conditionnelles. Cette formule est P2A inter B divisé par P2A. Nous trouvons donc que P2B sachant A est égal à 0,3 sur 0,6, ce qui est égal à 1,5. Pour mieux comprendre, il est possible de représenter ces événements dans un arbre qui montre les différentes possibilités. En résumé, ceci est une application basique de la formule des probabilités conditionnelles. N'hésitez pas à poser des questions si nécessaire. Maintenant, passons à la prochaine vidéo.
Maths SM&SP
Algèbre
2BAC SM Maroc

Application avec contexte
La probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de la marque A peut être calculée en utilisant la formule des probabilités conditionnelles.
Pour commencer, on sait que 60% des voitures fabriquées sont des voitures hybrides. Donc la probabilité d'avoir une voiture hybride est de 0,6, tandis que la probabilité de ne pas avoir une voiture hybride est de 0,4.
Ensuite, parmi les voitures hybrides, 70% d'entre elles sont de la marque A. Donc la probabilité d'avoir une voiture hybride de la marque A est de 0,6 * 0,7 = 0,42.
En utilisant ces informations, nous pouvons en conclure que la probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de la marque A est de 0,42.
Cette méthode utilise un arbre pour représenter les différents événements et permet de calculer la probabilité conditionnelle en utilisant la formule adéquate.
Maths SM&SP
Algèbre
2BAC SM Maroc
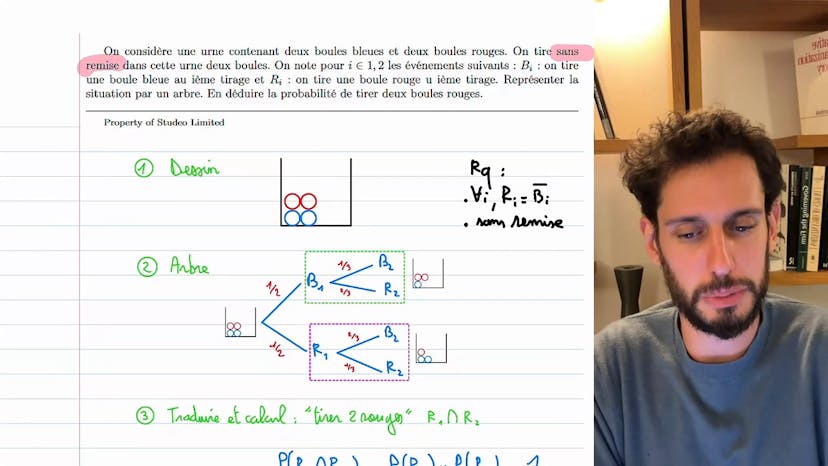
Arbre et urne sans remise
Dans ce cours, nous étudions une situation où nous tirons des boules d'une urne sans les remettre. Il est important de faire la distinction entre une situation avec remise (où l'on remet la boule après chaque tirage) et sans remise (où la boule tirée est retirée de l'urne). Cette distinction va influencer les probabilités tout au long du problème.
Nous utilisons les notations "bi" pour représenter le fait de tirer une boule bleue au ième tirage et "ri" pour représenter le fait de tirer une boule rouge. Vu qu'il n'y a que des boules bleues et rouges dans l'urne, nous pouvons remarquer que "ri" est équivalent à "bi barre" (le complémentaire de "bi"). Par exemple, si "b1" représente le fait de tirer une boule bleue au premier tirage, alors "r1" représente le fait de ne pas tirer une boule bleue au premier tirage (c'est-à-dire tirer une boule rouge).
L'idée ici est de représenter la situation par un arbre. Cela nous permet de visualiser plus clairement les différentes probabilités. En utilisant des dessins, nous pouvons rendre la situation plus compréhensible. Au fur et à mesure des tirages, nous modifions notre arbre pour refléter les probabilités en cours. Par exemple, si nous avons tiré une boule bleue au premier tirage, nous aurons alors une chance sur deux d'en tirer une deuxième, puis une chance sur trois d'en tirer une troisième.
Pour traduire cela en calculs, nous pouvons utiliser les probabilités conditionnelles. Par exemple, pour calculer la probabilité d'avoir tiré deux boules rouges, nous pouvons écrire "proba de R1 inter R2". Cette expression équivaut à la probabilité d'avoir tiré une boule rouge au premier tirage, puis dans cet univers, la probabilité d'avoir tiré une boule rouge au deuxième tirage.
En résolvant ces calculs, nous obtenons les probabilités recherchées. Dans cet exemple, la probabilité d'avoir tiré deux boules rouges est de 1/6. Il est important de bien comprendre les énoncés et de faire attention à la présence ou non de remise dans le problème.
N'hésitez pas à poser des questions si quelque chose n'est pas clair et je vous retrouve dans une prochaine vidéo.


