Home

MPSI/PCSI

Maths

Analyse

Applications & Relations

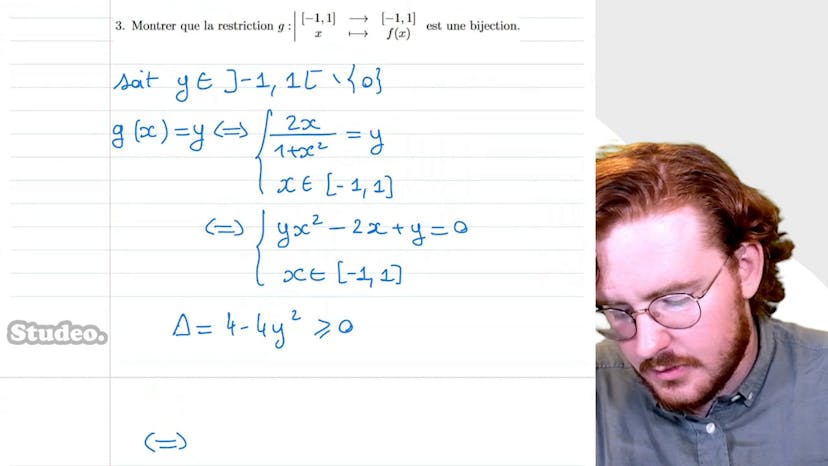
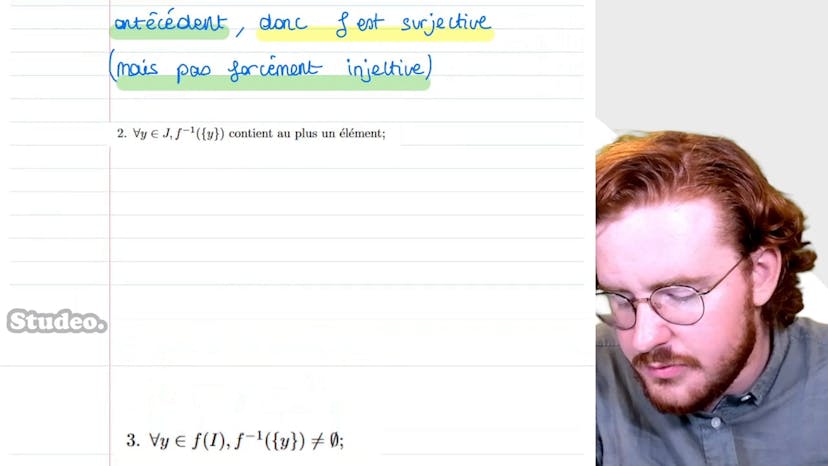
Dans cette vidéo, Paul aborde l'exercice sur la bijectivité et montre comment démontrer qu'une fonction est bijective. Il explique que pour prouver l'injectivité, il faut trouver des relations entre les nombres entiers, les diviseurs, et les nombres pairs et impairs. Pour prouver la surjectivité, il faut décomposer un nombre en facteurs premiers et trouver l'existence de son antécédent. À partir de là, il montre comment composer f avec une bijection de n étoiles dans n pour obtenir une bijection de n² dans n, en utilisant une application simple qui associe n à n-1. En résumé, l'exercice consiste à prouver la bijectivité d'une fonction et à trouver une bijection de n² dans n.

Salut c'est Paul! On se retrouve dans cette nouvelle vidéo où on va aborder un exercice sur la bijectivité et montrer qu'une fonction est bijective. C'est un exercice un peu avancé où il va falloir un peu se débrouiller par soi-même. On a cette fonction ici de n² dans n étoiles et qui associe n et p à 2 puissance n fois 2p plus 1. On doit démontrer que f est une bijection de n² dans n étoiles et après on va en déduire qu'une bijection de n² dans n. Donc f est bijective, c'est équivalent à f est injective et f est surjective. On va d'abord prouver l'injectivité. On va prendre des couples n, p, q, r tels que f, que leurs images sont égales et on va devoir prouver qu'on va devoir bidouiller. Et prouver que n, p, q, r. Pour ça il y a plusieurs façons. On va essayer de trouver des choses sur n, p, q, r. Il y aura des relations, des calculs. Les entiers, il faut toujours penser à l'arithmétique. Il faudra potentiellement faire appel à des choses sur les nombres pairs, impairs, les diviseurs, ce genre de choses. En parlant de choses sur les nombres pairs, impairs et les nombres entiers, pour démontrer que f est surjective, il va falloir décomposer k en 2n de p plus 1. Donc un nombre entier. On va avoir un nombre dans n étoiles ici et il va falloir prouver qu'il peut s'écrire sous la forme 2n fois 2p plus 1 pour prouver qu'il y a n et p les antécédents, mais qu'il n'y ait pas f. On peut remarquer que 2p plus 1 est un nombre impair. Et là on a un 2puissance n. 2puissance n fois 2p plus 1, il n'y a pas 36 000 décompositions dans les nombres entiers. Ça nous fait penser à la décomposition en facteur premier. On va sûrement utiliser ça pour s'en sortir. Parce que 2 ici est premier, donc là c'est déjà une partie de la décomposition en facteur premier. On attaque, on va d'abord démontrer l'injectivité. On prend deux couples d'éléments tels que leurs images par f sont égales. Et on va prouver que les couples sont égaux aussi. On écrit ce que ça veut dire que les images sont égales. Et là on va supposer sans perdre de généralité, donc ça va être utile pour la suite, que n est supérieur ou égal à m. Vu que m et n ont des rôles symétriques, on verra que ça n'a pas d'influence si n est inférieur ou égal à m dans l'autre cas. Si ça rajoute juste un k, on peut le supposer, le résultat est le même. On a deux puissances n-m, on le suppose pour que n-m soit supérieur ou égal à 0. Sinon on le mettrait juste de l'autre côté. On aurait m-n. C'est pour que deux puissances n-m soient un nombre entier, pour que la puissance 6 soit positive. On veut prouver ici que n est égal à m. Si par l'absurde on suppose que n est différent de m, ce nombre est un nombre paire. On peut extraire un 2 d'ici, ce n'est pas un puissance 0. La puissance est supérieur ou égal à 1. A droite, on remarque que c'est un nombre impair. Un nombre impair ne peut pas être à la fois impair et paire. Donc n est égal à m. On a aussi, entre autres, 2p plus 1 est égal à 2q plus 1. Donc p est égal à q. Ainsi, les coupes sont égaux. Donc f est injective. Aussi simple que ça. Maintenant, la surjectivité va être un peu plus compliquée. Parce qu'il y a cette histoire, il faut penser à la décomposition d'un facteur premier. On prend un k dans n étoiles et on veut prouver qu'il a un bien antécédent. On va décomposer k en produit de facteur premier. On fait apparaître ici le 2 comme le premier nombre premier de la décomposition. On va appeler la première puissance alpha 1, ici, on va l'appeler n. Sinon, il y a d'autres nombres premiers, ici avec des puissances. Ces nombres premiers sont distincts, ils sont tous différents de 2. Les p i supérieur ou égal à 2 sont des nombres premiers impaires. Parce que ces nombres premiers et sont différents de 2, donc ils sont impaires. Or, le produit de nombre impaire est impaire. Ici, c'est un produit de nombre impaire. Donc, ce nombre qui reste ici est impaire. On peut l'écrire sous la forme 2p plus 1. On a bien k égale 2 puissance n. On peut bien écrire k sous la forme 2 puissance n fois 2p plus 1 avec n et p des entiers naturels. On a bien l'existence de l'antécédent, donc f est surjective. On a l'objectivité de f de n² dans n étoiles. Maintenant, à partir de ça, on doit trouver une bijection de n² dans n. Il faut rajouter le 0. Comment on fait? Il faut se rappeler qu'une composition de 2 bijections est une bijection. Si on trouve une application, ici, la h de n étoiles dans n, une bijection de n étoiles dans n, il suffira de composer f avec cette application pour obtenir une bijection de n² dans n. f va de n² dans n étoiles et après on va de n étoiles dans n. Là, il faut que ce soit une bijection. Ici, on a une bijection, c'est f. Cette application est très simple. C'est l'application qui a n associé à n-1. Je ne vous fais pas la preuve que c'est une bijection, c'est assez évident. L'application h-f qui va de n² dans n, qui associe np à 2n 2p plus 1 moins 1, c'est une bijection de n² dans n. Parce que c'est une composition de bijections. Voilà, on a trouvé notre bijection et c'est la fin de l'exercice.

Bijection dans N

RELATED

Recommended videos

Injection, surjection : exemple

Injection, surjection : propriétés

Ensembles images