Online Révisions Maths lycée Courses by Top Instructors

Dérivabilité avec valeur absolue ?

Dans cet exercice, nous devons démontrer que la fonction donnée est continue et dérivable sur R, à l'exception du point x=0. Tout d'abord, nous commençons par vérifier que la fonction est définie sur R. En effet, peu importe la valeur de x, 1+x est strictement différent de 0, ce qui nous permet d'avoir une définition valide de la fonction. De plus, nous savons que le quotient de deux fonctions continues donne une fonction continue. Pour démontrer la continuité de la fonction, nous utilisons une calculatrice pour tracer son graphique et constatons qu'elle semble se rapprocher de 1 quand x tend vers l'infini et de -1 quand x tend vers moins l'infini. La fonction semble également relativement lisse, sans rupture de pente, ce qui soutient notre intuition de continuité. En ce qui concerne la dérivabilité de la fonction, nous supposons qu'elle est dérivable en x=0, car elle est clairement dérivable pour tous les autres points de R. En effet, x est dérivable sur R et 1+x en valeur absolue est dérivable partout sauf en 0. S'appuyant sur cette hypothèse, nous concluons que la fonction est dérivable sur tout R, à l'exception de x=0. Pour déterminer l'expression de la fonction en fonction du signe de x, cela est relativement simple. En vérifiant le comportement de la fonction en x=0, nous constatons qu'elle est bien continue, ce qui confirme notre expression. Enfin, pour justifier que la fonction est dérivable partout, sauf en x=0, nous utilisons le fait que x est dérivable et que le quotient de deux fonctions dérivables donne une fonction dérivable. Nous effectuons les calculs nécessaires pour dériver la fonction en x=0 et vérifions que le résultat est cohérent de chaque côté de ce point. Nous constatons que les dérivées de chaque côté de x=0 sont égales à 1, confirmant ainsi la dérivabilité de la fonction. En conclusion, nous démontrons que la fonction donnée est continue sur R et dérivable partout, sauf en x=0.

Équation Tangente

Dans ce cours, nous abordons la méthode de détermination des équations de tangentes, qui est une étape importante dans l'étude des fonctions. Il est essentiel de maîtriser cette méthode car elle est souvent utilisée dans les exercices où l'on doit étudier les tangentes et la position relative de la courbe par rapport à la tangente. Dans le premier exercice, nous devons étudier une fonction f, qui est égale à x^2 + 3x + 1. On nous demande de calculer f'(2) et f(2). Nous trouvons que f(2) = 11 et f'(2) = 7. En utilisant la formule y = f'(A) * (x - A) + f(A), où A est égal à 2, nous obtenons l'équation de la tangente, qui est y = 7x + 3. Ensuite, nous approfondissons la formule utilisée pour déterminer l'équation de la tangente. Nous démontrons que cette formule est simplement une équation de droite, y = mx + p, où m est le coefficient directeur et p est l'ordonnée à l'origine. En utilisant la connaissance de la tangente au point A, nous pouvons déduire que m = f'(A). Ensuite, en utilisant les coordonnées du point A, nous pouvons trouver p = f(A) - Af'(A). En regroupant ces résultats, nous obtenons l'équation de la tangente. Dans le deuxième exercice, nous devons étudier une nouvelle fonction g, qui est égale à e^x. On nous demande de trouver l'équation de la tangente à la courbe de g au point tapis 0. En calculant g'(0) = 1 et g(0) = 1, nous trouvons que l'équation de la tangente est y = x + 1. Il est important de bien maîtriser cette méthode car elle est fréquemment utilisée lors de l'étude des fonctions.

Formules Classiques

La dérivation est un rappel important en mathématiques. Il est essentiel de connaître parfaitement les formules de dérivation pour éviter des erreurs qui peuvent avoir un impact négatif sur les résultats d'un contrôle ou d'un examen. Il est donc crucial de s'assurer de la maîtrise de ces formules. Quelques exemples sont donnés pour illustrer l'utilisation des formules de dérivation. La dérivée de la fonction f(x) = 5x³ est 15x². Pour la fonction g(x) = (x^n)√(x), la dérivée est (n+1)x^(n-1) + (2/n)√(x). Pour la fonction h(x) = 1/v, la dérivée est -v'(x)/v², où v'(x) est la dérivée de v(x). Ensuite, l'utilisation des formules de dérivation est expliquée pour les cas du produit (u v) et du quotient (u/v). Pour le produit, la dérivée est u'v + uv'. Pour le quotient, la dérivée est (u'v - uv')/v². Des conseils méthodologiques sont donnés pour simplifier les calculs lors de la dérivation. Par exemple, le regroupement des termes de même degré est recommandé pour éviter des erreurs. Il est également utile d'utiliser des codes de couleur ou tout autre système de repérage pour faciliter la lecture et éviter d'oublier des termes importants. En conclusion, il est crucial de maîtriser les formules de dérivation et de les réviser régulièrement pour éviter des erreurs dans les calculs. Des méthodes méthodologiques, telles que le regroupement des termes de même degré, peuvent être utilisées pour éviter des oublis et des erreurs dans les calculs.

Polynômes 2nd Degré

Dans ce cours, on s'intéresse à l'étude d'un polynôme de degré 2. On cherche à aller plus vite que lors d'une étude classique de fonction. On commence par justifier l'ensemble de dérivabilité du polynôme, puis on calcule sa dérivée en utilisant les formules usuelles. On factorise si possible pour faciliter l'étude du signe de la dérivée. Ensuite, on déduit le tableau de variation en déterminant quand la dérivée change de signe. On calcule ensuite l'image au niveau de l'extremum qui est atteint en -b/2a. On sait déjà comment se comporte un polynôme de degré 2 grâce à la forme générale ax²+bx+c. Si a est positif, la courbe est en forme de "u" avec un minimum, et si a est négatif, la courbe est en forme de "n" avec un maximum. On peut utiliser ces informations pour aller plus vite dans l'étude du polynôme. On peut également utiliser les résultats classiques sur les polynômes de degré 2 pour trouver les coordonnées de l'extremum, l'ordonnée de l'extremum (-delta/4a), et les racines (-b+racine(delta)/2a et -b-racine(delta)/2a). Il est également important de remarquer que le minimum est au centre du polynôme et que les racines sont situées à égale distance du centre. Cette astuce permet de rapidement retrouver les résultats et de déduire le sens de variation et le signe de la fonction.

Étude f : Niveau MPSI mais outils de première !

Ce cours porte sur l'étude d'une famille de fonctions, notées f1, f2, etc., définies par f(x) = E(2x) / (x^n), où n est un entier naturel non nul. Le cours commence par déterminer le plus grand ensemble de définition de f, en excluant les valeurs de x pour lesquelles le dénominateur est nul. Ensuite, il est expliqué que f est dérivable sur tout son ensemble de définition, à l'exception de la valeur 0. Ensuite, le cours se concentre sur le cas où n est pair. On utilise la règle du produit et le comportement des puissances paires pour déterminer les variations de f, et on dresse le tableau de variation de f. Ensuite, les limites de f sont calculées en l'infini et en 0, et complétées dans le tableau de variation. Si n est impair, le comportement de f est différent. Les variations de f sont étudiées en utilisant le même raisonnement, et les limites en l'infini et en 0 sont calculées et ajoutées au tableau de variation. Le cours souligne également que l'étude de cas est essentielle dans l'exercice, en notant que les calculs seraient beaucoup plus difficiles sans la distinction entre n pair et n impair.

Composition : Déf

Dans cette vidéo, l'auteur explique ce qu'est la composition de deux fonctions en utilisant des exemples concrets. Il commence par décomposer une fonction en plusieurs étapes, en partant de x. Il explique que chaque étape consiste en une transformation de la fonction précédente. Par exemple, pour la fonction racine de x² plus 7, il passe successivement de x à x², puis de x² à x² plus 7, et enfin à la racine de x² plus 7. Il explique que cela revient à composer la variable x par trois fonctions simples. Ensuite, l'auteur donne une définition théorique de la composition de fonctions. Il explique que si on a deux fonctions U et V, où U est définie sur un intervalle i et à valeur dans un intervalle j, et V est définie sur j et à valeur dans un intervalle k, alors la composition de U et V, notée VU, est définie comme V de U de x. Autrement dit, on applique d'abord U à x, puis V au résultat obtenu. L'auteur mentionne également quelques propriétés de la composition de fonctions. Il explique que la composition de fonctions est associative, c'est-à-dire que (UV)W est égal à U(VW). Cependant, il précise que la composition de fonctions n'est pas commutative, c'est-à-dire que VU est généralement différent de UV. Pour illustrer cela, il donne l'exemple de deux fonctions U et V, où U est la fonction x² moins 7 et V est la fonction exponentielle. Il montre que VU et UV donnent des résultats différents, en prenant la valeur en 0 comme exemple. L'auteur conclut en rappelant l'importance de se rappeler que la composition de fonctions n'est pas commutative. Il encourage les spectateurs à poser des questions s'ils en ont, et les invite à se retrouver sur le forum pour discuter.

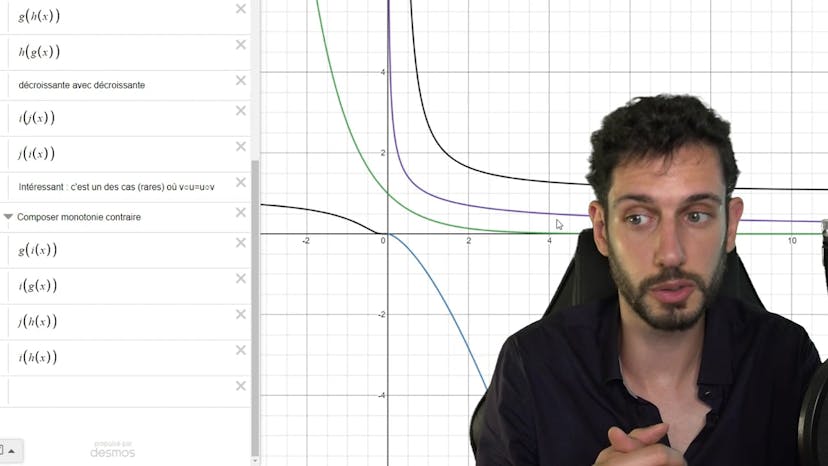
Dériver une composée

Dans cette vidéo, nous apprenons comment dériver une fonction composée. Nous commençons par expliquer ce qu'est la composition et les contraintes liées aux ensembles d'arrivée et de départ des fonctions composées. Ensuite, nous abordons les exemples les plus simples pour mieux comprendre le sujet. Par exemple, nous étudions la dérivée de 1/x et constatons que 1/u' ne correspond pas à la bonne formule, mais plutôt à -u'/u^2. Nous poursuivons avec d'autres exemples tels que la dérivée de racine de x et montrons que la bonne formule est (u'/2√u). Nous rappelons également les formules de dérivées de base, en insistant sur le fait qu'il faut toujours multiplier par u' lorsqu'il s'agit d'une fonction composée. Ensuite, nous donnons une définition formelle de la dérivée d'une fonction composée en utilisant les dérivées des fonctions u et v et en n'oubliant pas de multiplier par u'. Nous soulignons également qu'une conséquence intéressante est que si u et v ont la même monotonie, alors la fonction composée v∘u est croissante, tandis que si elles ont des monotonies contraires, la fonction composée est décroissante. Enfin, nous illustrons ces concepts avec des exemples concrets et montrons comment la monotonie des fonctions u et v affecte la monotonie de la fonction composée.

Fonction Composée

Dans ce cours, nous étudions une fonction composée et comment faire l'étude et le tableau de variation d'une fonction qui est composée de deux autres fonctions. Dans cet exemple, la fonction proposée est E2-1 sur x². Nous identifions les fonctions composantes de la fonction, g et h. La fonction g est -1 sur x², définie et dérivable sur R, tandis que la fonction h est l'exponentielle, définie et dérivable sur R. Nous utilisons les formules de dérivation pour trouver la dérivée de g, qui est 2 sur x³. Nous déterminons les variations de g en utilisant le signe de sa dérivée. Ainsi, on obtient un tableau de variation de g, qui est décroissante de moins l'infini à 0 et croissante de 0 à plus l'infini. Nous calculons également les limites de la fonction g, qui sont 0 en moins l'infini et moins l'infini en 0+. Ensuite, nous analysons la fonction h, qui est croissante sur R. En combinant les sens de variation de g et h, nous pouvons déduire les variations de la fonction composée, F. F sera donc décroissante sur R étoile moins et croissante sur R étoile plus. Nous calculons également les limites de F en utilisant les limites des fonctions composantes. La limite de F en moins l'infini est 1 et en plus l'infini est également 1. En 0, la limite de F est 0. Enfin, nous construisons le tableau de variation de F, qui est décroissante de 1 à 0 et croissante de 0 à 1. La fonction n'est pas définie en 0, mais peut être prolongée par continuité en posant F de 0 égale à 0. Une autre méthode aurait été de calculer directement la dérivée de F, mais nous avons choisi ici d'étudier l'intérieur de la composition. Si vous avez des questions, n'hésitez pas à les poser sur la FAQ.

Intuition et déf

Le cours explique les notions de convexité et de concavité. Il mentionne qu'une fonction est convexe lorsque sa courbe est en dessous de toute corde qui relie deux points de cette courbe. À l'inverse, une fonction est concave lorsque sa courbe est au-dessus de toute corde reliant deux points. La définition mathématique officielle est également introduite, mais il est souligné qu'il n'est pas nécessaire d'avoir une fonction continue et dérivable pour être convexe ou concave. La vidéo se termine en mentionnant que l'explication complète de la continuité sera abordée dans une prochaine vidéo.

Fonctions usuelles

Dans cette petite vidéo rapide, nous allons parler des fonctions classiques et de leurs caractéristiques. Tout d'abord, nous avons la fonction racine et la fonction log. Ces deux fonctions sont concaves, ce qui signifie que leur graphique a une certaine courbe vers le bas. D'autre part, nous avons également les fonctions x carré et exponentielle x, qui sont convexes. Leur graphique a une forme de sourire, ce qui indique qu'ils sont généralement convexes. Ensuite, nous pouvons dire que la fonction 1 sur x est convexe sur r plus étoile et concave sur r moins étoile. Pour vérifier cela, il faut tracer leurs graphiques respectifs. En bonus, si nous nous concentrons sur r plus (la partie droite du graphique), nous pouvons retenir une règle hors programme. Si nous prenons un alpha positif et que nous considérons les fonctions x puissance alpha avec alpha entre 0 et 1, nous obtenons des fonctions qui ressemblent à la racine carrée et qui sont concaves. D'autre part, les fonctions x puissance alpha avec alpha supérieur à 1 (comme x carré ou x cubique) sont convexes. Si nous explorons r moins, la convexité des fonctions dépendra de la parité de la puissance (x2, x4, x6 seront convexes, tandis que x3, x5, etc seront concaves). En résumé, nous pouvons dire que les racines sont toujours concaves, les puissances supérieures à 1 sont toujours convexes et lorsque la puissance est égale à 1, la fonction est une droite qui peut être à la fois convexe et concave. En traçant quelques exemples de fonctions x puissance alpha avec différents alpha, nous pouvons observer ces caractéristiques. En conclusion, ce cours rapide sur les fonctions classiques peut vous donner une bonne culture générale sur le sujet. N'hésitez pas à poser des questions si nécessaire.

Inégalité fondamentale

Dans cette vidéo, nous allons étudier la relation entre une courbe et ses sécant. Nous avons déjà vu qu'une fonction convexe est située en dessous de ses sécant. Pour illustrer cela, nous pouvons observer le graphe suivant : une courbe rouge située sous des sécant bleues. Pour traduire cette relation, nous allons comparer la différence d'ordonnée entre un point sur le segment bleu et un point sur le segment rouge, pour une même abscisse située entre les abscisses A et B. Nous allons comparer ces deux points : celui sur le segment et celui sur la courbe rouge. L'idée est de démontrer que lorsque nous avons une fonction convexe, le point situé sur le segment a une ordonnée plus élevée que le point de même abscisse situé sur la courbe rouge. Cette inégalité sera un élément important de notre étude. Avec ces informations en tête, nous pouvons introduire un point d'abscisse intermédiaire entre A et B. Nous allons nommer ce point T, situé entre 0 et 1. En pondérant les abscisses de A et de B, nous pouvons calculer une moyenne. Ensuite, nous comparons l'image de ce point intermédiaire par la fonction F (la courbe rouge) avec l'image de cette abscisse par l'équation du segment bleu (la sécant). La difficulté dans cette démonstration est de montrer que cette expression, TF2X + (1-T)F2Y, correspond bien à l'image du point d'abscisse intermédiaire sur le segment. La démonstration complète est un peu complexe, mais si vous êtes intéressé, je peux la présenter dans une autre vidéo. En résumé, nous avons montré que pour une fonction convexe, le point intermédiaire entre deux points sur la sécant a une ordonnée plus élevée que le point correspondant sur la courbe. Cette inégalité est une traduction directe de la différence de position entre la courbe et la sécant. De plus, il existe un lien logique entre convexité et concavité : si une fonction est convexe, sa fonction inverse est concave et vice versa. N'hésitez pas à poser vos questions dans le forum et je vous retrouve dans la prochaine vidéo bonus pour la démonstration complète.