 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

Division euclidienne
Dans cette vidéo, Paul explique la division euclidienne de moins 534 par 6. Il rappelle que la division euclidienne est représentée par l'équation moins 534 égale à 6 fois Q plus R, où moins 534 est le dividende, 6 est le diviseur, Q est le quotient et R est le reste. Le but est de trouver le quotient et le reste. En posant la division, on commence avec moins 53 et -8 x 6 pour obtenir moins 48, il reste donc moins 5. En descendant le 4, on a moins 54 et -9 x 6 donne 54, il reste donc 0. Donc le quotient est -89 et le reste est 0. Ainsi, la division euclidienne de moins 534 par 6 est moins 534 égale à moins 89 fois 6 plus 0. Il est recommandé d'écrire plus 0 lorsque le reste est présent pour bien comprendre l'écriture de la division euclidienne. C'est la fin de l'exercice et on se dit à la prochaine fois.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

CAPITAL : Reste de 145²⁰²² par 7 ?
Dans cet exercice de congruence, nous devons trouver le reste de la division de 145 puissance 2022 par 7. Tout d'abord, nous simplifions 145 en ignorant la puissance 2022 et en calculant 145 modulo 7, ce qui donne un reste de 5.
Ensuite, nous étudions les différentes puissances de 5 pour comprendre s'il existe un cycle. Nous remarquons qu'après quelques puissances, nous obtenons toujours les mêmes restes : 3, 4, 6, 2, 3, 4. Nous comprenons alors qu'il y a un cycle et nous pouvons l'écrire sous forme de table de congruence.
Pour déterminer le reste de 145 puissance 2022, nous devons regarder la puissance 2022 dans la table. En observant les différentes cases, nous remarquons que 2022 est divisible par 6 et donc se trouve dans la première case. Nous pouvons donc conclure que 145 puissance 2022 est congru à 5 puissance 2022 qui est congru à 1.
En résumé, après avoir simplifié 145 et étudié les puissances de 5, nous trouvons que 145 puissance 2022 est congru à 1. Il est important de comprendre cette méthode et de l'utiliser pour résoudre d'autres exercices de congruence et d'arithmétique similaires.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

Divisibilité et fraction
Dans cette vidéo, l'exercice consiste à déterminer pour quelles valeurs entières de n (différentes de 4) la fraction 35/(n-4) est un nombre entier. Le piège réside dans le fait que n est un entier relatif et non un entier naturel ou positif.
Pour résoudre cet exercice, il est important de rappeler que l'on travaille dans l'ensemble Z des entiers relatifs. On cherche donc les diviseurs de 35 pour trouver les valeurs possibles de n-4.
Les diviseurs de 35 sont : 1, 5, 7 et 35. On doit également prendre en compte les valeurs négatives : -1, -5, -7 et -35. Puisque n doit être différent de 4, on exclut cette valeur de nos réponses possibles.
Donc si n-4 appartient à l'ensemble des diviseurs de 35, n doit prendre les valeurs 5, 9, 11 et 39 pour les quatre premiers diviseurs, et les valeurs -31, -3, -1 et 3 pour les quatre derniers diviseurs.
En résumé, les valeurs de n pour lesquelles la fraction 35/(n-4) est entière sont 5, 9, 11, 39, -31, -3, -1 et 3.
Il est essentiel de faire attention au contexte et à la nature des variables lors de la résolution de ces types d'exercices pour éviter les erreurs et maximiser les points obtenus.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

Divisibilité de n⁵-n ?
Ce cours porte sur la factorisation d'une expression mathématique. L'objectif est de démontrer que l'expression, a^n = n^5 - n, est divisible par certains nombres tels que 2, 3 et 5.
Pour commencer, l'instructeur suggère de simplifier l'expression en la factorisant dès le début. En factorisant par n, l'expression devient n * (n^4 - 1). Il est également possible de reconnaître une identité remarquable, n^4 - 1 = (n^2 - 1) * (n^2 + 1). Ainsi, l'expression peut être réécrite comme n * (n^2 - 1) * (n^2 + 1).
Ensuite, pour démontrer que a^n est pair, l'instructeur utilise le fait que le produit de deux entiers consécutifs sera toujours divisible par 2. Puisque n, n-1 et n+1 sont des entiers consécutifs, cela garantit que a^n est pair.
Pour démontrer que a^n est divisible par 3, l'instructeur fait remarquer que parmi les entiers consécutifs n-1, n et n+1, il y en aura toujours un qui sera un multiple de 3. Par conséquent, leur produit, a^n, sera également divisible par 3.
Enfin, pour démontrer que a^n est divisible par 5, l'instructeur utilise une table de congruence. Il montre que pour chaque valeur de n (0, 1, 2, 3, 4), le produit n * (n-1) * (n+1) * (n^2 + 1) est congruent à 0 modulo 5. Ainsi, cela prouve que a^n est divisible par 5.
En conclusion, l'approche de factorisation dès le début permet de simplifier les démonstrations et de trouver rapidement les diviseurs de l'expression. Cette méthode d'investissement initial facilite l'ensemble des questions posées dans cet exercice.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI
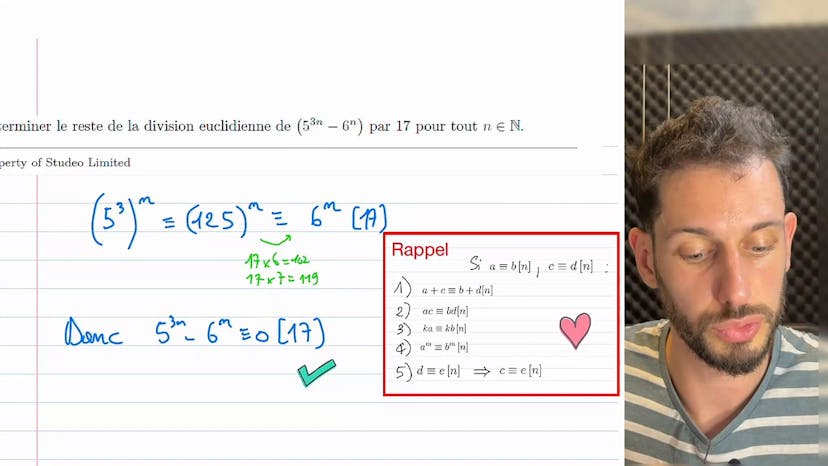
Reste de 5³ⁿ - 6ⁿ par 17 ?
Dans cet exercice, nous devons trouver le reste de la division Euclidienne de "5 puissance 3n moins 6 puissance n" par 17. Pour cela, nous pourrions créer des tables de congruence pour les valeurs de 5 et de 6 pouvant être élevées à des puissances (3n et n respectivement) et les comparer avec le modulo 17. Cependant, il est préférable d'analyser les deux éléments de la différence séparément pour voir s'il y a quelque chose de plus simple qui se passe.
Nous avons donc le calcul de "5 puissance 3n" qui peut être simplifié en utilisant la propriété que si A est congru à B, alors A puissance M est congru à B puissance M. Donc, nous pouvons simplifier 125 à l'aide du modulo 17 en enlevant les paquets multiples de 17. Par exemple, nous pouvons enlever 102, puis 102 plus 17 jusqu'à ce que nous atteignions un nombre proche de 125.
Ensuite, nous comparons "5 puissance 3n moins 6 puissance n" avec 0, nous remarquons que les deux éléments sont congrus entre eux modulo 17. Par conséquent, nous pouvons conclure que 17 divise toujours cette différence.
En résumé, pour trouver le reste de la division Euclidienne de "5 puissance 3n moins 6 puissance n" par 17, nous avons réalisé une analyse des congruences en simplifiant les valeurs utilisant le modulo 17 et en comparant les éléments de la différence. Nous avons conclu que 17 divise toujours cette différence.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

Un entier toujours impair ?
Dans cet exercice, nous devons démontrer que la quantité 3n4 + 5n1 est impaire pour tout n. Nous appelons cette quantité "n" pour la suite de la question. Nous devons également en déduire que ce nombre n'est jamais divisible par n(n+1).
Pour commencer, nous pouvons remarquer que n(n+1) évoque les notions de sommes d'entiers jusqu'à n et de produits de deux nombres consécutifs. La somme des entiers jusqu'à n est égale à n(n+1)/2, ce qui peut nous aider à aborder le problème. De plus, un produit de deux nombres consécutifs inclut toujours un nombre paire.
En utilisant ces réflexes, nous pouvons dire que si n(n+1) divise n, alors 2 divise n. Cependant, si n est impair, alors ce n'est pas possible. Donc, grâce à cette réflexion, nous pouvons conclure que n(n+1) ne divise jamais n.
Maintenant, nous nous concentrons sur le fait que n doit être impair. Puisque nous avons une addition de 1 à la fin de la quantité, nous pouvons la simplifier en disant que si n est impair, alors en enlevant 1, n devient pair. Donc, montrons plutôt que la quantité n que j'appelle "a" est paire.
Pour cela, nous factorisons n en 3n3 + 5. Nous pensons à une possible décomposition de 2k pour n. Il peut être 2k, 2k+1 ou 2k+2. Cependant, nous devons considérer la division paire-impair.
Si n est pair, alors a est pair et la démonstration est terminée. Si n est impair, nous pouvons écrire n congru à 1 modulo 2. Dans ce cas, nous remarquons que n³ est aussi congru à 1 modulo 2, donc 3n³ est congru à 3 modulo 2 (car 3 modulo 2 est égal à 1). En ajoutant 5, nous obtenons 0, ce qui signifie que si n est impair, 3n³ + 5 est pair.
En conclusion, si n est pair, a est pair, et si n est impair, a est pair. Par conséquent, a n'est jamais divisible par n(n+1) car il est pair tandis que n(n+1) contient un multiple de 3 et donc de 6.
Voilà, c'est la fin de cet exercice. Si vous avez des questions, n'hésitez pas à les poser dans les commentaires. À bientôt pour une autre vidéo !
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

Piège à éviter : degré 2 !
Dans ce cours, il est expliqué comment résoudre l'équation x² plus x congruent à 3 modulo 5 pour x entier. L'exercice peut sembler difficile et effrayant, mais il faut simplement réfléchir calmement. Le professeur suggère de réécrire x² plus x comme n² plus n pour faciliter la compréhension. Ensuite, il explique que la méthode classique consiste à tester tous les cas possibles en utilisant une table des congruences. Il suggère également de vérifier s'il y a une factorisation évidente, bien que cela ne semble pas être le cas dans cet exercice. Ensuite, il explique comment remplir rapidement la table des congruences, en calculant x² modulo 5 et la somme de 2 modulo 5 pour chaque valeur de x de 0 à 4. En analysant les résultats, il conclut que pour toutes les valeurs de x, x² plus x est congruent à 0, 1 ou 2, et jamais à 3. Par conséquent, l'ensemble des solutions est vide. Malgré l'apparente complexité de l'exercice, le professeur souligne l'importance d'une approche méthodique et réfléchie. Il espère que cette explication aidera les élèves et leur donne rendez-vous pour une prochaine vidéo.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

5²ⁿ, 2²ⁿ ... et des congruences !
Dans cet exercice de congruence, nous devons déterminer quand l'expression 145 puissance 2022 modulo 17 est divisible par 3.
Tout d'abord, nous simplifions en se concentrant sur les congruences de 5 puissance n modulo 3. Nous remarquons que 5 puissance n est congruent à 2 puissance n modulo 3. De plus, nous observons que 5 puissance 2n est congruent à 4 puissance n. Ainsi, nous pouvons simplifier en disant que 5 puissance 2n est toujours congruent à 1.
Ensuite, nous examinons la somme de 5 puissance 2n, 5 puissance n et 1 modulo 3. Cette somme est congruente à 2 puissance n plus 2. En analysant le tableau de congruence de 2 puissance n, nous constatons que si n est pair, alors 2 puissance n est congruent à 1.
En résumé, l'expression 145 puissance 2022 modulo 17 est divisible par 3 si et seulement si n est pair.
Dans un deuxième exercice similaire, nous devons déterminer quand l'expression 2 puissance 2n plus 2 puissance n plus 1 est divisible par 7. Nous simplifions cette expression en utilisant les congruences de 4 puissance n et 2 puissance n. Le tableau de congruence de 4 puissance n nous montre que si n est multiple de 3, alors 4 puissance n est congruent à 1. De même, le tableau de congruence de 2 puissance n indique que si n est multiple de 3, alors 2 puissance n est congruent à 1.
En conclusion, l'expression 2 puissance 2n plus 2 puissance n plus 1 est divisible par 7 pour tous les entiers n qui ne sont pas multiples de 3.
Il est important de noter que ces méthodes de congruence sont fondamentales et peuvent s'appliquer à d'autres exercices plus complexes.
Révisions Maths lycée
Arithmétique Maths expertes
MPSI/PCSI

Problème : Suite et PGCD !
Ce cours traite d'un problème d'arithmétique intéressant qui commence avec une fraction, ce qui est inhabituel car on préfère travailler avec des entiers. On définit A_n comme étant une suite. On effectue quelques calculs pour trouver A2 et A3. Ensuite, on cherche à démontrer que A_n+1 peut s'écrire de manière récurrente. On effectue des calculs et constatons que cela est vrai. Ensuite, on démontre que A_n appartient à N (l'ensemble des entiers naturels) en utilisant une récurrence triviale. La question 4 aborde le calcul du PGCD de A_n et A_n+1 et montre qu'il est égal à 1 ou à 3. Enfin, on vérifie que A0 est congru à 1 modulo 3 et on conclut que A_n n'est jamais divisible par 3. On déduit ainsi que le PGCD est égal à 1. Cette approche permet d'obtenir une solution efficace à l'exercice.


