Cours de BAC 2022 en Ligne par les Meilleurs Professeurs - BAC 2022

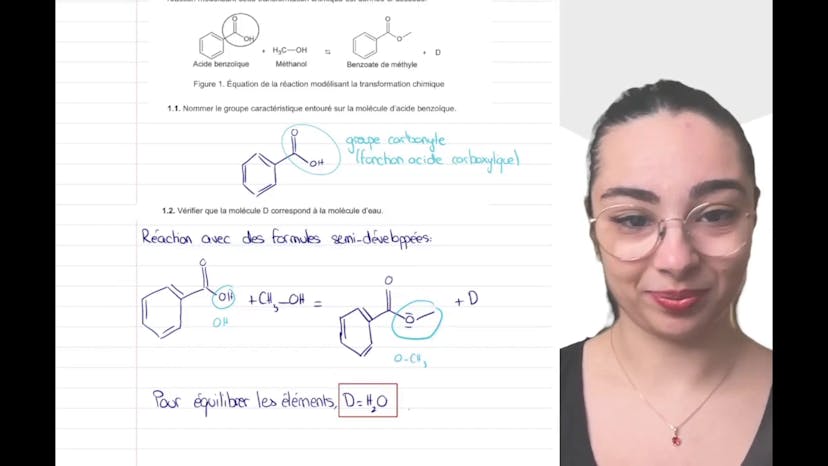
Synthèse d’un ester à odeur florale (1)

Aujourd'hui, nous allons étudier la synthèse d'un estère à odeur florale. Cette réaction consiste à synthétiser le benzoate de méthyl à partir de l'acide benzoïque et du méthanol. Le premier objectif est de nommer le groupe caractéristique sur la molécule d'acide benzoïque, qui est le groupe carbonyl COOH, également appelé fonction acide carboxylique. Ensuite, nous devons vérifier si la molécule D correspond bien à la molécule O, qui est un sous-produit de la réaction. Pour ce faire, nous examinons les éléments chimiques présents dans les molécules et concluons que tous ceux qui ne se trouvent pas dans les molécules écrites sont présents dans D. L'équilibre des molécules nous montre que le OCH3 est égal à H2O. Pour la suite de cette synthèse, nous vous invitons à regarder la partie 2 de la vidéo.

Synthèse d’un ester à odeur florale (2)

Le cours aborde la deuxième partie du sujet de BAC sur la synthèse d'un estère à odeur florale. Il explique le rôle de l'acide sulfurique dans le protocole de synthèse en tant que catalyseur pour augmenter la vitesse de la réaction. Ensuite, il présente les montages utilisés pour chauffer à reflux et explique l'utilité d'un réfrigérant à boules pour éviter les pertes de réactifs. Le chauffage à reflux permet d'augmenter la vitesse de la réaction et d'éviter de perdre de la matière. Le cours aborde également les pictogrammes de sécurité et les précautions opératoires à prendre lors de la manipulation des produits chimiques. Le choix d'ajouter de l'eau salée dans l'étape 2 est expliqué en raison de la solubilité des produits à éliminer de la phase aqueuse. Les espèces chimiques contenues dans chaque phase sont identifiées, ainsi que l'équation montrant comment l'ajout de solution aqueuse d'hydrogénocarbonate de sodium permet de transformer l'acide benzoïque en benzoate.

Synthèse d’un ester à odeur florale (3)

Salut à tous ! Aujourd'hui, nous continuons à traiter de la synthèse d'un estère, dans le cadre du sujet de Pâques de Polynésie 2022. Nous nous intéressons maintenant à l'identification de la molécule par spectroscopie infrarouge. La spectroscopie infrarouge ne permet pas de déterminer exactement la molécule, mais peut donner des indices et éliminer certaines possibilités. Nous observons une bande CO, entre 1650 et 1740, avec une forte intensité d'absorption, ce qui correspondrait à l'estère que nous étudions. Nous repérons également une autre bande CO, entre 1000 et 1300, qui pourrait correspondre à une autre partie de la molécule. Nous identifions également les bandes CH, qui indiquent la présence de la chaîne carbonée. En revanche, nous ne détectons pas la bande OH, qui confirme que les réactifs de départ (acide carboxylique et alcool) ont bien réagi et disparu lors de la synthèse. En résumé, nous observons les bandes CO et CH, ainsi que la liaison simple C-O. Nous ne détectons pas la bande OH, ce qui suggère l'absence d'acide benzoïque. J'espère que ce résumé vous a été utile ! À bientôt pour la suite du cours.

Synthèse d’un ester à odeur florale (4)

Le cours traite de la synthèse d'un ester et de la détermination du rendement de cette synthèse. L'objectif est de déterminer les quantités de réactifs nécessaires et de montrer comment améliorer le rendement de la réaction. Le cours commence par récapituler les étapes de la synthèse et les considérations expérimentales. Ensuite, le produit de la réaction est identifié à l'aide du spectre infrarouge. La partie principale du cours porte sur les questions de rendement. Il est expliqué comment calculer les quantités de réactifs nécessaires à partir des masses et des masses moléculaires. L'importance des conversions entre les masses et les masses moléculaires est soulignée. L'utilisation de l'analyse dimensionnelle est également mentionnée comme une méthode utile. Le concept de proportions stoichiométriques est expliqué, et il est rappelé qu'il faut faire attention aux coefficients dans l'équation de la réaction. Un tableau d'avancement est ensuite complété pour représenter la progression de la réaction. Les quantités de matière des différentes espèces à l'état final sont calculées en utilisant les données expérimentales. Le rendement de la synthèse est ensuite estimé à environ 67%. Enfin, des suggestions pour améliorer le rendement de la synthèse sont données. Il est expliqué qu'il faut introduire un excès de réactifs et éliminer l'eau au fur et à mesure du processus de réaction. Le procédé de Dean-Stark est mentionné comme une méthode pour éliminer l'eau. En conclusion, ce cours traite de la détermination du rendement d'une synthèse d'un ester, en expliquant les étapes nécessaires pour calculer les quantités de réactifs et en donnant des suggestions pour améliorer le rendement.

Synthèse d’un ester à odeur florale (5)

Le cours traite d'un exercice de synthèse d'esters et de dosage spectrophotométrique. L'objectif est de déterminer la quantité de matière en ion benzoate à l'aide d'un dosage spectrophotométrique. Le cours explique d'abord qu'il faut régler le spectrophotomètre à la longueur d'onde où l'absorbance est maximale, c'est-à-dire 270 nm. Ensuite, il présente les différents domaines spectraux (violet, rouge, infrarouge, ultraviolet) avec les longueurs d'onde correspondantes. Ensuite, le cours aborde la dilution de la solution obtenue après la synthèse. Il explique qu'il faut diluer 100 fois cette solution pour obtenir la solution S3. Il précise également l'importance de connaître la concentration et le volume pour réaliser une dilution précise. Enfin, le cours présente les mesures spectrophotométriques et utilise la loi de Beer-Lambert pour trouver la concentration de la solution S3. Il explique ensuite que la solution a été diluée 100 fois, ce qui permet de retrouver la concentration de la solution après la synthèse. Cette concentration correspond à la quantité de matière restante en ion benzoate et en acide benzoïque. Le cours conclut en précisant que cet exercice est noté sur 10 points et qu'il faut environ deux heures pour le traiter. Il mentionne également qu'il reste deux autres exercices optionnels à traiter.

Un tracteur gravitationnel pour dévier un astéroïde (1)

Bonjour à tous, Laila de Studio ici. Aujourd'hui, nous allons faire l'exercice A du sujet de physique de l'année dernière, Polynésie 2022, jour 1. Cet exercice porte sur la gravitation et utilise la loi de Newton, le champ de gravitation et la loi de Kepler. Nous devons dévier un astéroïde qui se dirige vers la Terre en utilisant un tracteur gravitationnel. Dans cet exercice, nous devons représenter la force gravitationnelle exercée par l'engin spatial sur l'astéroïde. Cette force est attractive, ce qui signifie que l'engin spatial attire l'astéroïde. La durée de cette interaction gravitationnelle est très courte par rapport à la période orbitale de l'astéroïde, ce qui signifie que nous pouvons considérer la trajectoire de l'astéroïde comme presque rectiligne. L'engin spatial reste à une distance constante de l'astéroïde pour cette même raison. Nous devons faire un schéma de la trajectoire de l'astéroïde et représenter les variations des vecteurs vitesse. Nous devons également déterminer la direction dans laquelle l'engin spatial doit être placé pour dévier l'astéroïde de sa trajectoire. Pour cela, nous utilisons la troisième loi de Newton qui nous indique que la force exercée doit être dans la même direction que la variation de vitesse. Nous devons donc placer l'engin spatial dans la direction de cette variation de vitesse pour dévier l'astéroïde au maximum. J'espère que cette vidéo vous a été utile. Dans la prochaine vidéo, nous aborderons la seconde partie de l'exercice et étudierons plus en détail le fonctionnement du tracteur gravitationnel.

Un tracteur gravitationnel pour dévier un astéroïde (2)

Dans cette partie du cours, Leïla explique la déviation d'un astéroïde appelé Apophis et son impact sur la Terre. Elle commence par donner l'expression de la norme de la force exercée par l'engin spatial sur Apophis en fonction de gMd. Cette force est de 0,2 N. Ensuite, elle applique la deuxième loi de Newton dans le référentiel héliocentrique pour trouver l'expression de Δt en fonction de Δv, qui est Δt= gm/d^2. Elle explique ensuite que les scientifiques ont estimé qu'il fallait augmenter la norme du vecteur vitesse de 2x10^-6 m/s au niveau de l'aphélie, et demande la durée Δt d'utilisation dans ce cas. En faisant les calculs, elle trouve que Δt est égal à 96 heures ou 4 jours. Leïla indique également que l'utilisation du tracteur gravitationnel augmente le rayon de la trajectoire de l'astéroïde, ce qui affecte la période. Elle établit ensuite la troisième loi de Kepler pour Apophis dans le référentiel héliocentrique, en utilisant le principe fondamental de la dynamique et en raisonnant sur les périodes. Elle obtient l'expression R^3/T^2 = GMs/(4π^2). Ensuite, elle détermine la valeur de la période de révolution T' après l'utilisation du tracteur gravitationnel, en prenant en compte une augmentation de 15 minutes. En utilisant la loi de Kepler, elle calcule le nouveau rayon de la trajectoire, qu'elle trouve être 1,37 x 10^11 mètres. Finalement, elle calcule l'écart de rayon, qui est de 3 x 10^6 mètres, pour montrer le changement de trajectoire de l'astéroïde. Leïla conclut en soulignant l'importance de ces concepts pour comprendre les forces gravitationnelles.

Eclipse solaire du 10 juin 2021 (1)

Dans ce cours, Léa aborde l'exercice sur l'éclipse solaire qui est tombée au Bac l'année dernière en Polynésie. Elle explique que cet exercice fait partie des exercices optionnels du Bac de Physique. Elle souligne également que l'exercice concerne l'optique géométrique et plus particulièrement la lunette astronomique. Léa présente brièvement la lunette astronomique comme un instrument à focale composé de deux lentilles convergentes. Ensuite, Léa passe à la résolution de l'exercice. Elle explique que la première étape consiste à identifier les termes "objectif" et "oculaire" dans la figure de la lunette de Galilée. Elle indique que la lentille L1 est l'objectif car elle est la plus proche de l'objet observé, tandis que la lentille L2 est l'oculaire car elle est proche des yeux. Léa poursuit en demandant aux étudiants de donner le nom scientifique du point P où les rayons se croisent pour la lentille L1. Elle rappelle que les rayons se croisent au foyer principal image de la lentille L1. Ensuite, Léa aborde l'éclipse du 10 juin 2021 et fournit les données techniques de construction de la lunette utilisée. Elle explique qu'il faut positionner le foyer principal objet de la deuxième lentille au même endroit que le foyer principal image de la première lentille pour que la lunette soit afocale. Léa répond ensuite à une question sur le passage d'un rayon lumineux issu de B infini à travers le centre optique O1 de la lentille L1. Elle explique qu'un rayon qui traverse le centre optique d'une lentille n'est pas dévié et trace le rayon lumineux correspondant sur un schéma. 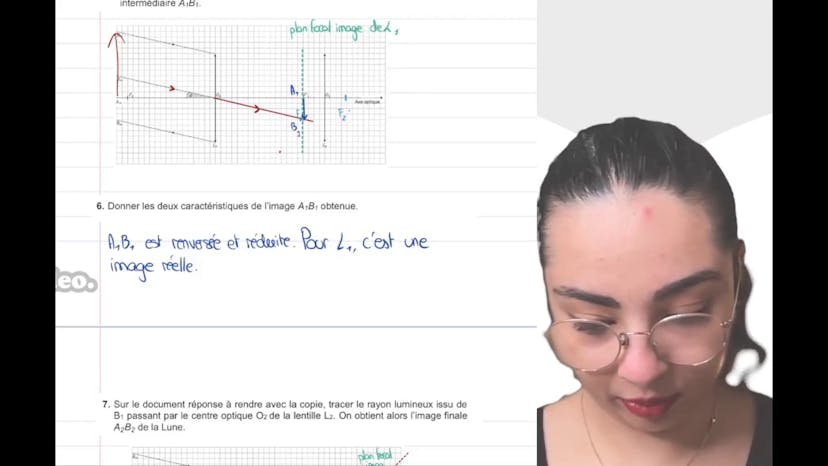Léa poursuit en demandant aux étudiants de donner les caractéristiques de l'image obtenue (A1-B1). Elle mentionne que l'image est renversée et réduite, et précise que c'est une image réelle car les rayons se croisent effectivement. Ensuite, Léa demande aux étudiants de tracer le rayon lumineux issu de B1 passant par le centre optique O2 de la lentille L2 pour obtenir l'image finale A2-B2 de la lune. Elle explique que ce rayon-là n'est pas dévié et que son image ressort à l'infini car il se trouve dans le plan focal objet de la lentille L2. Enfin, Léa demande aux étudiants de représenter le faisceau de rayons lumineux issus de B-infini passant par les bords des lentilles L1 et L2. Elle explique que les rayons se croisent tous au point B pour former une image intermédiaire, puis ressortent parallèles car l'objet est à l'infini. Léa conclut en précisant que cet exercice aura été utile et annonce qu'elle continuera la suite dans une prochaine vidéo.

Eclipse solaire du 10 juin 2021 (2)

Dans cette vidéo, Laila termine l'exercice B du sujet Polynésie 2022, jour 1, qui traite de la lunette astronomique. Elle explique qu'il faut positionner l'angle theta prime pour observer l'image finale de la Lune à travers la lunette, et que le grossissement de la lunette est donné par theta prime sur theta. Elle utilise des approximations pour déterminer le grossissement en se basant sur les triangles formés par les lentilles. En utilisant les valeurs des focales de l'objectif et de l'oculaire données dans l'encadré, elle calcule un grossissement de 73, qui est cohérent avec la valeur maximale proposée par le fabricant de la lunette. Ensuite, elle aborde le sujet de l'éclipse et du diamètre de la Lune par rapport au Soleil. Elle utilise des schémas et des calculs trigonométriques pour déterminer le diamètre de la Lune, qui est environ 3,56 fois 10 puissance 3 km. Elle compare cette valeur avec celle donnée dans l'article, qui est d'environ 3,48 fois 10 puissance 3 km, et conclut que l'écart est probablement dû à des approximations dans l'article. Elle termine en encourageant les spectateurs à poser des questions et en annonçant la prochaine vidéo où elle abordera l'exercice C.

Acoustique d’une salle (1)

Le cours aborde la diffraction des ondes lumineuses et sonores dans le contexte de l'acoustique d'une salle. Dans la première partie, on étudie une expérience sur la diffraction des ondes lumineuses, en utilisant un laser et une fente. On détermine que l'angle caractéristique de diffraction est θ = λ/a, où λ est la longueur d'onde et a est la largeur de la fente. On montre ensuite que la largeur de la tâche de diffraction est L = 2λd/a, en utilisant des approximations géométriques. On mesure la largeur L en faisant varier la taille de la fente a, et on obtient une relation linéaire de la forme L = k/a. En utilisant une autre relation donnée dans la question précédente, on exprime k en fonction de λ et D, où D est la distance entre la fente et l'écran. On nous demande ensuite de montrer que λ = 6,5x10^-7 mètres en interprétant un graphique et en calculant le coefficient directeur de la droite correspondante. On détermine également les angles θ1 et θ2 correspondant aux largeurs a1 = 38 micromètres et a2 = 150 micromètres respectivement, en utilisant la formule θ = λ/a. On conclut que la diffraction est plus marquée pour la fente de taille a1, car l'angle de diffraction θ1 est plus grand que θ2. On donne rendez-vous pour la suite du cours dans une prochaine vidéo qui abordera la diffraction sonore.

Acoustique d’une salle (2)

Dans cette vidéo, Layla de Studio aborde la dernière partie de l'exercice C du sujet Polynésie 2022 jour 1, qui traite de la diffraction des ondes sonores. Elle explique que la diffraction des ondes sonores fonctionne de la même manière que celle des ondes lumineuses et cela est étudié à travers l'acoustique d'une salle de concert. Layla commence par expliquer que lors d'un concert, un élève constate qu'il perçoit mieux les sons graves de fréquence f1 (200 hertz) que les sons aigus de fréquence f2 (1 kilohertz). Pour comprendre cela, elle rappelle la formule pour exprimer la longueur d'onde lambda d'une onde sonore en fonction de la vitesse du son V son et de la fréquence f, qui est lambda = V son / f. En utilisant cette formule, Layla montre que les longueurs d'onde lambda 1 (pour f1) et lambda 2 (pour f2) ont des valeurs respectives de 1,70 mètres et 0,340 mètres, en appliquant les valeurs données dans l'énoncé. Ensuite, Layla présente la situation à laquelle l'élève doit réfléchir. Il y a une scène de concert avec un pilier important pour l'étude acoustique. L'élève peut se trouver à trois positions : A, B ou C. Il doit choisir la position qui correspond le mieux à sa perception des sons graves par rapport aux sons aigus. Pour cela, Layla explique que la diffraction joue un rôle crucial. En utilisant le pilier comme obstacle, la diffraction se produit différemment selon les fréquences. Si la largeur du pilier est beaucoup plus petite que la longueur d'onde, la diffraction se produit de manière similaire à celle d'une fente étroite dans une expérience de diffraction de la lumière. Layla explique que les sons graves, avec une longueur d'onde plus élevée (lambda 1 ), seront plus diffractés que les sons aigus, avec une longueur d'onde plus petite (lambda 2). Elle visualise les différentes positions (A, B et C) par rapport au pilier et explique que la position C correspondrait le mieux à la situation décrite par l'élève lors du concert, car les sons graves seront plus diffractés, mais les sons aigus peuvent ne pas être perceptibles. Layla conclut en soulignant que cet exercice nécessite une application des connaissances sur les ondes lumineuses et une analogie avec les ondes sonores. Elle espère que cet exercice a été utile et encourage les personnes à continuer à réviser pour le bac de physique qui approche.

Synthèse d’un ester à odeur florale (1)

Aujourd'hui, nous allons étudier la synthèse d'un ester à odeur florale, qui est un exercice de chimie tombé au bac en Polynésie l'année dernière. L'objectif est d'étudier une réaction de synthèse et de réfléchir ensemble au protocole expérimental. La réaction que nous allons réaliser est la synthèse du benzoate de méthyl à partir d'acide benzoïque et de méthanol. La première étape consiste à nommer le groupe caractéristique entouré sur la molécule d'acide benzoïque, qui est un groupe carbonyl COOH, correspondant à la fonction acide carboxylique. Ensuite, nous devons vérifier que la molécule D correspond bien à la molécule O, c'est-à-dire les sous-produits de la réaction. Pour cela, nous examinons les éléments chimiques et constatons que tous ceux qui ne sont pas déjà présents dans les molécules écrites se retrouvent dans D. Nous remarquons que la molécule reste inchangée jusqu'à un certain point. Le groupement OH de l'acide benzoïque se transforme en un groupement OCH3 dans D. De plus, le méthanol est présent dans la molécule CH3OH. Ainsi, pour équilibrer ces molécules, D doit être égal à H2O. La suite de cette synthèse sera abordée dans une prochaine vidéo.

Synthèse d’un ester à odeur florale (2)

Le sujet du cours porte sur la synthèse d'un ester à odeur florale. Dans la première partie du cours, on a étudié les fonctions caractéristiques de la molécule à synthétiser. Dans cette deuxième partie, on se penche sur le protocole de synthèse en répondant à des questions expérimentales. Tout d'abord, on nous demande de déterminer le rôle de l'acide sulfurique ajouté dans l'étape 1 du protocole. En général, de petites quantités d'additifs n'ont pas de rôle direct dans la réaction, mais peuvent servir de catalyseurs pour accélérer la vitesse de la réaction. Ensuite, on nous demande d'identifier le montage correspondant à l'étape 1 du protocole. Le chauffage à reflux, consistant à chauffer le contenu d'un ballon sans rien perdre, se fait à l'aide d'un chauffe-ballon et d'un réfrigérant à boules. Le montage B répond à ces critères. Le chauffage à reflux présente deux intérêts principaux : il augmente la vitesse de la réaction et évite les pertes de matière. Ensuite, on nous demande d'analyser les pictogrammes de sécurité et de justifier les précautions prises. Les pictogrammes utilisés indiquent que des précautions doivent être prises en portant des gants, des blouses en coton et des lunettes de protection. De plus, il est recommandé de travailler sous une hotte pour ne pas inhaler les éventuelles vapeurs toxiques dégagées par les produits chimiques utilisés. On nous demande également d'expliquer pourquoi de l'eau salée est ajoutée à l'étape 2 du protocole. L'ajout d'eau salée permet de séparer les produits indésirables présents dans la phase aqueuse, tels que l'acide benzoïque, du produit recherché, qui lui reste dans la phase organique. L'eau salée favorise la séparation des deux phases. Pour finir, on nous demande de rédiger la réaction permettant de transformer l'acide benzoïque en benzoate en ajoutant de la solution aqueuse d'hydrogénocarbonate de sodium. La réaction se fait par un échange de protons : l'acide benzoïque réagit avec l'hydrogénocarbonate de sodium pour donner du benzoate et de l'acide carbonique. Cette réaction permet d'éliminer l'acide benzoïque de la phase organique. En résumé, cette partie du cours porte sur le protocole de synthèse de l'ester à odeur florale. On a étudié le rôle de l'acide sulfurique, identifié le montage correspondant à l'étape 1, expliqué les précautions de sécurité à prendre, justifié l'ajout d'eau salée dans l'étape 2 et rédigé la réaction transformant l'acide benzoïque en benzoate.

Synthèse d’un ester à odeur florale (3)

Dans ce cours, nous continuons l'exercice 1 du sujet de Pâques de Polynésie 2022 sur la synthèse d'un estère. L'objectif est d'identifier la molécule obtenue par spectroscopie infrarouge. On observe une bande CO entre 1650 et 1740, ce qui indique la présence de l'estère recherché. Une autre bande d'absorption forte entre 1000 et 1300 correspond également à la CO. On observe également des bandes fines multiples pour les CH, ce qui confirme la présence de la chaîne carbonée. En revanche, on ne détecte pas de bande OH, ce qui suggère que les réactifs de départ ont bien été éliminés lors de la synthèse. En résumé, on identifie les bandes CO, CH et absence de bande OH, ce qui confirme la formation de la liaison C=O et l'élimination des réactifs.

Synthèse d’un ester à odeur florale (4)

Bonjour à tous, ici Leïla de Studio. Aujourd'hui, nous allons continuer notre exercice de synthèse d'un ester qui a été réalisé l'année dernière lors de Pâques. Pour récapituler les parties précédentes, nous avons déjà identifié les différentes étapes de la synthèse, justifié le protocole et abordé les considérations expérimentales. Dans la partie 3, nous avons identifié le produit de notre synthèse à l'aide d'un spectre infrarouge. Maintenant, nous allons nous intéresser aux questions de rendement. Il est important de savoir non seulement quel produit nous avons fabriqué, mais aussi dans quelle quantité cela a été fait, pour que cela soit intéressant pour nous. Nous disposons des masses molaires nécessaires, nous rappelons la réaction chimique et à l'aide des données de l'étape 1 du protocole de synthèse, nous devons déterminer les quantités de réactif, appelées NAlcool et NAcide, utilisées dans la réaction. Pour cela, nous devons utiliser les formules de conversion entre les masses et les masses molaires. Personnellement, je n'ai pas toutes ces formules en tête, mais j'utilise une approche basée sur l'analyse dimensionnelle pour vérifier leur validité. En utilisant les données dont nous disposons, nous pouvons dire que la quantité initiale d'alcool est de 99 millimoles. Soyez attentifs aux conversions entre les masses et les masses molaires, car c'est souvent là que se trouve le piège dans les exercices numériques. Il est important de vérifier que tout est cohérent. Nous utilisons la même méthode pour l'acide. Donc ici, cela sera MAcide / MAcide, et nous obtenons 100 millimoles. Nous en déduisons ensuite que les réactifs ont été introduits dans des proportions stœchiométriques. Cela signifie que ces réactifs disparaissent à la même vitesse dans le tableau d'avancement. Ce terme signifie simplement que la quantité divisée par le coefficient stœchiométrique est la même. Pour résumer, nous avons trouvé que la quantité initiale d'alcool était d'environ 99 millimoles et la quantité initiale d'acide était d'environ 100 millimoles. Ensuite, on nous demande de compléter le tableau d'avancement. Ce tableau présente les états initial, intermédiaire et final de la réaction. Nous avons donc deux ou trois lignes, selon la configuration. Dans l'état initial, nous énumérons les réactifs introduits, c'est-à-dire l'acide et l'alcool, et rien d'autre. Dans l'état intermédiaire, nous notons les réactifs consommés en soustrayant X, où X est l'avancement de la réaction. Nous notons également les produits formés, c'est-à-dire l'eau et l'ester, avec X comme coefficient. Pour l'état final, nous remplaçons X par XF, qui est notre avancement final. Le tableau d'avancement est un outil essentiel pour suivre l'évolution d'une réaction. Ensuite, nous devons déterminer les quantités de matière de toutes les espèces présentes à l'état final, qui sont notées NAcide-X, NAlcool-X et NEster-X. Nous avons déjà calculé la quantité d'ester expérimentale, qui est de 9,11 grammes, ce qui correspond à environ 67 millimoles. Nous savons également que la quantité d'eau formée est similaire à celle de l'ester, soit 67 millimoles. Cette information, associée au tableau d'avancement, nous permet de déterminer les quantités restantes des réactifs, qui sont environ 33 millimoles pour l'acide et 32 millimoles pour l'alcool. Ensuite, nous devons montrer que le rendement de la synthèse approche les 67%. Le rendement est le rapport entre la quantité obtenue et la quantité maximale théorique. Dans ce cas, nous avons calculé que nous avons obtenu 67 millimoles d'ester et la quantité maximale théorique est de 100 millimoles. Par conséquent, le rendement est d'environ 67%. Enfin, nous devons proposer une méthode pour améliorer le rendement de la synthèse. Dans l'idéal, nous voudrions atteindre un rendement de 100%. Pour cela, nous devons examiner le coefficient de la réaction, Ka. Nous pouvons augmenter les quantités de réactifs en excès et réduire la quantité d'eau formée, car elle perturbe l'équilibre de la réaction en limitant la formation de l'ester. Une méthode efficace pour éliminer l'eau au fur et à mesure de la réaction est le procédé Dean-Stark. J'espère que cette synthèse du cours vous a été utile. N'hésitez pas à poser vos questions dans les commentaires. À bientôt pour la partie finale de cet exercice.

Synthèse d’un ester à odeur florale (5)

Dans cette vidéo, Leïla explique comment réaliser un dosage spectrophotométrique pour vérifier la quantité de matière en ion benzoate dans une solution, dans le cadre d'un exercice. Elle précise que cette méthode de dosage est souvent utilisée car elle est simple. Elle explique que l'ion benzoate est obtenu à partir de l'acide benzoïque grâce à l'hydrogénocarbonate de sodium. Le but est de déterminer la quantité de matière restante en ion benzoate dans la phase aqueuse en utilisant un spectrophotomètre. Leïla explique qu'il est nécessaire de régler le spectrophotomètre à la longueur d'onde d'absorbance maximale. Elle donne des indications sur les longueurs d'onde correspondant aux différents domaines du spectre électromagnétique, afin d'identifier cette longueur d'onde maximale. Ensuite, elle décrit les étapes du dosage spectrophotométrique, qui consiste à diluer la solution obtenue après la synthèse. Elle souligne l'importance de prendre en compte les dilutions lors des mesures. Elle explique comment préparer une solution S3 en diluant la solution mère S0 dans une fiole jaugée de 100 ml. Leïla donne les mesures spectrophotométriques et montre comment utiliser la loi de Birlambert pour retrouver la concentration en ion benzoate. Elle explique que la solution a été diluée 100 fois, ce qui permet de retrouver la concentration finale en utilisant la concentration mesurée précédemment. Enfin, elle conclut que la quantité de matière d'ion benzoate restante est de 3,3 x 10^-2 mol, ce qui correspond également à la quantité de matière d'acide benzoïque restante. Elle termine en précisant que cet exercice est noté sur 10 points et recommande de compter environ deux heures pour le traiter. Elle rappelle également qu'il y a deux autres exercices optionnels à choisir.

Un tracteur gravitationnel pour dévier un astéroïde (1)

Dans cette vidéo, Laila de Studio résume l'exercice A du sujet de physique de l'année dernière, Polynésie 2022, jour 1, qui traite de la gravitation. L'exercice concerne l'utilisation d'un tracteur gravitationnel pour dévier un astéroïde et fait référence aux lois de Newton, au champ de gravitation et à la loi de Kepler. Laila explique que l'engin spatial exerce une faible force sur l'astéroïde pour modifier son orbite et éviter une collision avec la Terre. Elle commence par une étude générale de la déviation de l'astéroïde, représentant la force gravitationnelle exercée par l'engin spatial sur l'astéroïde. Elle explique que cette interaction gravitationnelle se produit pendant une durée delta t, qui est très courte par rapport à la période orbitale de l'astéroïde. L'astéroïde est considéré comme ayant une trajectoire quasiment rectiligne pendant cette durée. L'engin spatial se maintient à une distance constante de l'astéroïde pour cette raison. Laila demande ensuite aux spectateurs de faire un schéma représentant les variations des vecteurs vitesse, en expliquant que l'objectif est de vérifier que la somme de la vitesse initiale et de la variation de vitesse est égale à la vitesse finale. Elle mentionne également qu'il y a une direction privilégiée dans laquelle l'engin spatial doit être placé pour dévier l'astéroïde de sa trajectoire, et explique que cette direction est celle de la variation de vitesse. Elle justifie cette réponse en utilisant la troisième loi de Newton. En conclusion, Laila annonce qu'elle traitera de la seconde partie de l'exercice dans une prochaine vidéo.

Un tracteur gravitationnel pour dévier un astéroïde (2)

Le cours porte sur la déviation d'un astéroïde appelé Apophis à l'aide d'un tracteur gravitationnel. Dans la première partie, la force d'interaction gravitationnelle entre l'engin spatial et l'astéroïde est calculée, donnant une valeur de 0,2 N. Ensuite, la deuxième loi de Newton est appliquée dans le référentiel héliocentrique pour obtenir une expression de la durée d'utilisation Δt en fonction de la variation de vitesse Δv. Ensuite, on estime qu'une augmentation de 2 x 10-6 m/s de la norme du vecteur vitesse est suffisante pour dévier l'astéroïde. La durée d'utilisation Δt dans ce cas est calculée en utilisant les valeurs données dans l'énoncé. On nous dit également que l'utilisation du tracteur gravitationnel augmente le rayon de la trajectoire de l'astéroïde, ce qui peut éviter l'impact avec la Terre. La troisième loi de Kepler est établie pour Apophis dans le référentiel héliocentrique, reliant le rayon et la période de l'astéroïde. Enfin, la valeur de la période de révolution après l'utilisation du tracteur gravitationnel est calculée en ajoutant une augmentation de 15 minutes à la période initiale. Utilisant la loi de Kepler, le nouveau rayon de la trajectoire est calculé, ainsi que l'écart de rayon entre l'ancienne et la nouvelle trajectoire. La correction de cet exercice permet de revoir des notions importantes telles que la force gravitationnelle, la loi de Kepler et le principe fondamental de la dynamique.

Eclipse solaire du 10 juin 2021 (1)

Aujourd'hui, nous allons corriger un exercice sur l'éclipse solaire qui est tombé au Bac l'année dernière en Polynésie. Cet exercice fait partie des exercices optionnels au Bac de Physique. Il porte sur l'optique géométrique et plus précisément sur la lunette astronomique. La lunette astronomique est un instrument à focale composé de deux lentilles convergentes, l'objectif et l'oculaire. Dans la première question, il est demandé d'identifier ces deux termes, ce qui est assez simple à faire. Ensuite, il est demandé de donner le nom scientifique du point où les rayons se croisent pour la lentille L1, il s'agit du foyer principal image. Le texte parle ensuite de l'éclipse du 10 juin 2021 et donne des informations techniques sur la construction de la lunette. On nous demande ensuite de réaliser des constructions. Tout d'abord, on nous demande de positionner le foyer principal objet et le foyer principal image pour une lunette commerciale afocale. Pour cela, il faut que ces deux foyers coïncident, ce qui signifie que les rayons qui les traversent convergent en un point précis. Ensuite, on nous demande de tracer le rayon lumineux issu d'un point B infini passant par le centre optique O1 de la lentille L1. Ce rayon n'est pas dévié et permet d'obtenir l'image intermédiaire B'1. Ensuite, on nous demande de donner les caractéristiques de cette image, qui est réelle, renversée et réduite. Ensuite, on nous demande de tracer le rayon lumineux issu de B'1 passant par le centre optique O2 de la lentille L2 pour obtenir l'image finale, A2, B2 de la lune. Enfin, on nous demande de représenter le faisceau de rayons lumineux issus de B infini passant par les bords des lentilles L1 et L2. Pour cela, il faut tracer les rayons qui se croisent en un point précis et ressortent parallèles, en prenant en compte le point de convergence B. Voilà, c'était un résumé de l'exercice sur l'éclipse solaire et la lunette astronomique.

Eclipse solaire du 10 juin 2021 (2)

Dans cette vidéo, Laila termine l'exercice B sur la lunette astronomique du sujet Polynésie 2022, jour 1. Elle explique qu'il s'agit de questions plus théoriques pour déterminer le grossissement de la lunette. Elle demande aux élèves de positionner l'angle theta prime où est observée l'image finale de la Lune à travers la lunette. Le grossissement de la lunette est défini comme étant theta prime sur theta, avec les angles theta et theta prime étant petits. On peut donc faire l'approximation que tan theta est à peu près égal à theta et tan theta prime est à peu près égal à theta prime. En utilisant la géométrie des triangles formés par les rayons, elle montre comment exprimer le grossissement comme étant égal à A1, B1 fois F1 prime sur F2 prime. Elle propose ensuite aux élèves de calculer la valeur du grossissement pour la lunette utilisée en utilisant les valeurs des focales de l'objectif et de l'oculaire données dans l'énoncé. Le grossissement obtenu est de 73, ce qui est cohérent avec la valeur maximale proposée par le fabricant. Ensuite, Laila aborde le contexte général de l'utilisation de la lunette, notamment en ce qui concerne l'éclipse. Elle explique que la Lune a un diamètre 400 fois plus petit que celui du Soleil, mais elle est aussi 400 fois plus proche de la Terre, ce qui permet un recouvrement presque parfait lors d'une éclipse. Laila donne des directives aux élèves pour déterminer le diamètre de la Lune. Elle suggère de commencer par dessiner un schéma et d'utiliser la trigonométrie pour obtenir une expression reliant le diamètre de la Lune (petit d) au diamètre du Soleil (D) et à l'angle alpha. En utilisant cette relation, elle obtient un diamètre de la Lune de 3,56 fois 10 puissance 3 km. L'article mentionne que le diamètre de la Lune est 400 fois plus petit que celui du Soleil, ce qui correspond à une valeur de 3,48 fois 10 puissance 3 km. L'écart entre les deux valeurs peut être dû à des approximations faites dans l'article. Laila conclut en encourageant les élèves à poser leurs questions dans les commentaires et annonce qu'elle reviendra dans une prochaine vidéo pour l'exercice C.

Acoustique d’une salle (1)

Dans cette vidéo, Leïla du Studio aborde l'exercice C du sujet Polynésie 2022 jour 1 sur l'acoustique d'une salle. Elle commence par expliquer qu'il s'agit d'un exercice de diffraction, d'abord pour les ondes lumineuses puis pour les ondes sonores dans le contexte de l'acoustique d'une salle. Dans la première partie, l'exercice présente une expérience sur la diffraction des ondes lumineuses. Un laser de longueur d'onde inconnue est dirigé vers une fente de largeur irréglable, et un écran est placé à une certaine distance. Le montage expérimental est similaire à celui qui est étudié dans les cours. L'angle caractéristique de la diffraction est donné par θ = λ/a, où θ est en radian, λ est la longueur d'onde, et a est la largeur de la fente. En utilisant l'approximation des petits angles, on peut simplifier cette expression en θ ≈ λ/a. En utilisant de la géométrie, on peut montrer que la largeur L de la tâche de diffraction est donnée par L = 2λd/a. En faisant varier la taille a de la fente, on mesure la largeur L de la tâche centrale et obtient une relation linéaire entre L et 1/a, c'est-à-dire L = k(1/a). On nous demande alors de montrer que cette relation linéaire est justifiée. Leïla explique qu'il y a plusieurs façons de le faire, mais ici elle a choisi de placer les points sur un graphique représentant L en fonction de 1/a, et montre que la courbe est bien une droite passant par l'origine. Il est important de préciser que la droite passe par l'origine pour éliminer toute possibilité d'une ordonnée à l'origine arbitraire. En utilisant la relation L = k(1/a) donnée dans la question précédente, on peut exprimer k en fonction de λ et 2d. Ensuite, l'exercice demande de montrer que la longueur d'onde λ est égale à 6,5 x 10^-7 mètres. Pour cela, il faut interpréter le graphique et utiliser l'expression de k obtenue précédemment. Leïla explique qu'il s'agit de trouver le coefficient directeur de la droite représentée par le graphique, c'est-à-dire la pente de la droite. Elle utilise la formule k = Δy/Δx où Δy est la variation en hauteur et Δx est la variation en longueur. En prenant les points appropriés sur le graphique, elle obtient une valeur pour k, qui permet ensuite de calculer la valeur de λ recherchée. Enfin, l'exercice demande de déterminer la valeur de l'angle θ2 correspondant à une autre fente de longueur a2 = 150 micromètres, sachant que l'angle θ1 correspondant à la fin de la largeur a1 = 38 micromètres est égal à 1,7 x 10^-2 radians. On utilise la même formule que précédemment, c'est-à-dire θ2 = λ/a2, où λ est connu. On calcule θ2 et on constate que θ1 > θ2, ce qui signifie que la diffraction est plus marquée pour la fente de longueur a1. En conclusion, Leïla espère que cette vidéo a été utile et donne rendez-vous pour la suite de l'exercice sur la diffraction sonore.