 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Suites
- Limites des Fonctions
- Continuité et Dérivabilité
- Dérivation
- Convexité
- Logarithme
- Fonctions Trigonométriques
- Primitives & Équations Différentielles
- Calcul Intégral
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Suites
- Limites des Fonctions
- Continuité et Dérivabilité
- Dérivation
- Convexité
- Logarithme
- Fonctions Trigonométriques
- Primitives & Équations Différentielles
- Calcul Intégral
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

Continuité en un Point
Apprendre à trouver des dérivées de fonctions ayant plusieurs expressions sur des intervalles différents est l'objectif de cette méthode. On apprendra qu'une fonction peut être continue mais pas forcément dérivable, et dans ce cas, il est important de vérifier la continuité en différents points de la fonction. Pour qu'une fonction soit continue, elle doit d'abord être définie et ensuite, elle doit être continue sur tous les points de l'intervalle, y compris les extrémités. Pour vérifier cela, on doit regarder les limites à gauche et à droite de chaque point de l'intervalle, ainsi que la limite de la fonction en ce point. Si toutes les conditions sont remplies, la fonction est continue. Dans les prochaines étapes, on abordera la dérivation de cette fonction.
Maths Spé
Analyse
Terminale

Dérivabilité en un Point
La fonction étudiée dans ce cours est f(x) = |x|^2 + 2x - 3. On constate par observation graphique que cette fonction n'est pas dérivable en x = -3 et x = 1. On peut expliquer cela par le fait que la valeur absolue introduit une discontinuité de pente en ces points. Cependant, f(x) est dérivable sur l'ensemble des autres points de R. Cette dérivabilité peut être justifiée en montrant que f(x) est une composition de deux fonctions continues, à savoir un polynôme et la fonction valeur absolue.
Maths Spé
Analyse
Terminale

Prolongement par Continuité
Le prolongement par continuité est une méthode importante en mathématiques. Il est utilisé lorsque nous avons une fonction qui n'est pas définie en un point A, mais qui a une limite définie quand x tend vers A. Nous pouvons alors prolonger la fonction en A par continuité. Pour ce faire, nous posons f(A) égale à la limite de f(x) quand x tend vers A. Cela crée une fonction qui est définie et continue en A. Par exemple, la fonction f(x) égale x sur x n'est pas définie en 0, mais a une limite égale à 1. Nous pouvons prolonger cette fonction en faisant f(0) = 1. Dans l'exercice donné, la fonction proposée est f(x) égale à sinus 1 sur x pour x différent de zéro, et f(0) = 0. Nous devons prouver que cette fonction est bien continue en 0. Pour ce faire, nous utilisons le théorème d'encadrement en montrant que la valeur absolue de f(x) est encadrée entre 0 et x. Puis, nous prouvons que la valeur absolue de f(x) tend vers 0 quand x tend vers 0. En utilisant le théorème d'encadrement, nous montrons que la limite de f(x) quand x tend vers 0 est bien égale à 0, ce qui prouve que la fonction est bien continue en 0.En utilisant des méthodes mathématiques comme le théorème d'encadrement, nous pouvons prouver que les fonctions prolongées par continuité sont bien définies et continues.
Maths Spé
Analyse
Terminale

TVI et Fonction Auxiliaire
La méthode consiste à utiliser le théorème des valeurs intermédiaires pour étudier une fonction complexe. La fonction donnée est f(x) = 10x / (e^x + 1). On commence en calculant la dérivée de f(x), avec laquelle on obtient la fonction g(x) = 1 - xe^x. On vérifie que g(x) est continue sur l'intervalle [0,+∞], et qu'elle est strictement décroissante grâce à sa dérivée g'(x) = -xe^x < 0. En utilisant le théorème des valeurs intermédiaires pour les fonctions strictement monotones, on peut trouver un unique réel α tel que g(α) = 0. On détermine que α est compris entre 1,29 et 1,28. En utilisant le tableau de signes de la dérivée de f(x), on peut déduire le sens de variation de f(x), qui est croissante sur [0,α] et décroissante sur [α,+∞]. La fonction a un maximum en α et tend vers 0 en +∞. La stricte monotonie est importante pour assurer l'unicité de l'antécédent zéro, et donc pour appliquer le théorème des valeurs intermédiaires pour les fonctions strictement monotones.
Maths Spé
Analyse
Terminale
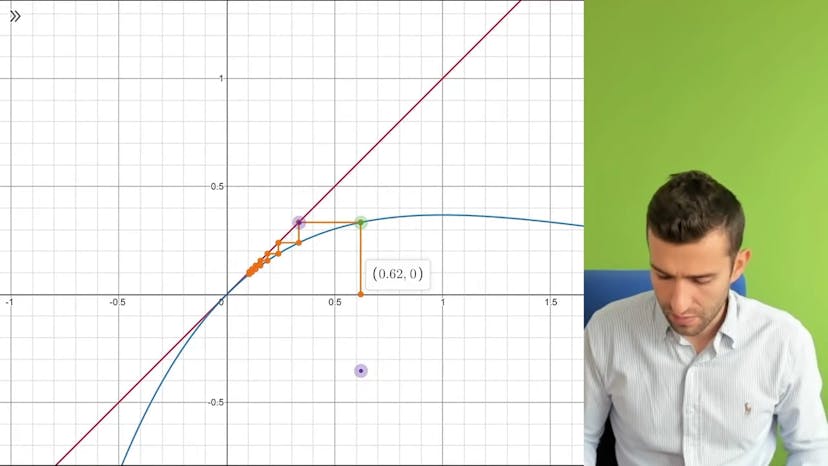
Continuité et suites 1
Dans cette méthode de calcul de limite avec suites définies par récurrence, il faut vérifier les hypothèses pour bien trouver la limite et la justifier. La suite est convergente vers une limite L si la relation de récurrence type un+1=f(un) vérifie que si la suite converge vers une limite L, alors un+1 converge aussi, en passant à la limite. Cela nécessite que f soit continue. En cherchant les points fixes, solutions de l'équation f(x)=x, on peut trouver la solution de la limite qui peut être unique ou multiple suivant la fonction f. Il faut alors être vigilant sur la continuité de f pour éviter les erreurs. Le premier terme de la suite est essentiel, car le comportement de la suite dépend de sa valeur. Si le premier terme est négatif et que la suite diverge, alors la solution de la limite est impossible.
Maths Spé
Analyse
Terminale

Continuité et Suites 2
Dans ce cours, nous étudions les suites définies par récurrence, en nous intéressant à leur limite. Nous commençons par associer une fonction f à la suite, telle que n+1 soit égal à f(n). Pour résoudre cette équation, nous devons étudier la continuité de f. Pour ce type d'exercice, la continuité de f est essentielle. Ensuite, nous résolvons l'équation f(x) = x pour trouver les valeurs possibles de la limite de la suite. Nous étudions également la dérivabilité de f. Il est important de noter que f peut ne pas être définie en certains points, ce qui impacte sa croissance. Nous passons ensuite à la démonstration par récurrence que 0.5 < u1 < u1+1 < 3. Nous utilisons la propriété de croissance de f pour composer avec l'hypothèse de récurrence. Nous concluons que la suite est croissante et bornée. En utilisant ces informations, nous déduisons que la suite converge vers une limite L. Enfin, nous soulignons l'importance de la continuité de f pour pouvoir affirmer que la limite est bien une solution de l'équation f(x) = x.
Maths Spé
Analyse
Terminale

Déf formelle
Ce cours traite de la continuité des fonctions en mathématiques. La définition informelle de la continuité est que si une fonction peut être tracée sans lever le stylo, elle est continue. La définition formelle de la continuité en un point est que la limite finie de f (x) lorsque x s'approche de a est égale à f (a). La limite finie en un point est atteinte lorsque l'on peut trouver un couloir de taille arbitraire, dans lequel toutes les valeurs de la fonction pour les x dans ce couloir sont comprises dans une zone définie. Si cela est possible pour n'importe quelle taille de couloir, la limite finie est atteinte, et si la limite finie est f (a), la fonction est dite continue en ce point.
Maths Spé
Analyse
Terminale

Discontinuités : exemples
La continuité d'une fonction est définie par une limite finie en un point qui est égale à la valeur de la fonction en ce point. Si pour un couloir fixé, toutes les valeurs de la fonction dans un couloir vertical atteignent le couloir orange, alors la fonction est continue. La discontinuité peut survenir pour diverses raisons, comme la non-existence d'un point ou une saute soudaine dans la fonction. Si la discontinuité est basée sur l'impossibilité de définition, comme dans le cas de 1/x en 0, alors la fonction n'est même pas continue. Si la discontinuité est rattrapable, comme dans le cas du sinus sur x avec un point ajouté en 0, alors la fonction est considérée comme prolongeable par continuité.
Maths Spé
Analyse
Terminale

Fonctions usuelles
Ce cours explique les fonctions continues, qui sont celles qui ne présentent pas de saut ou de trou dans leur graphique. Les fonctions les plus courantes sont continues, comme les fonctions racine carrée, exponentielle, sinus et cosinus. Les fonctions construites à partir de combinaisons ou de compositions de fonctions continues sont également continues. Les fonctions non continues sont souvent créées par morceaux et par branches. Il y a différents types de discontinuité, comme la discontinuité par définition (exemple : 1/x n'est pas défini en 0), les sauts de discontinuité, les discontinuités prolongeables et les discontinuités en un point mal placé non-prolongeables. Enfin, l'ensemble de définition (l'ensemble sur lequel une fonction est définie), l'ensemble de continuité (où une fonction est continue) et l'ensemble de dérivabilité (où une fonction est dérivable) ne sont pas toujours égaux pour une fonction donnée. Par exemple, la fonction valeur absolue de x est continue sur R, mais n'est pas dérivable sur R.
Maths Spé
Analyse
Terminale
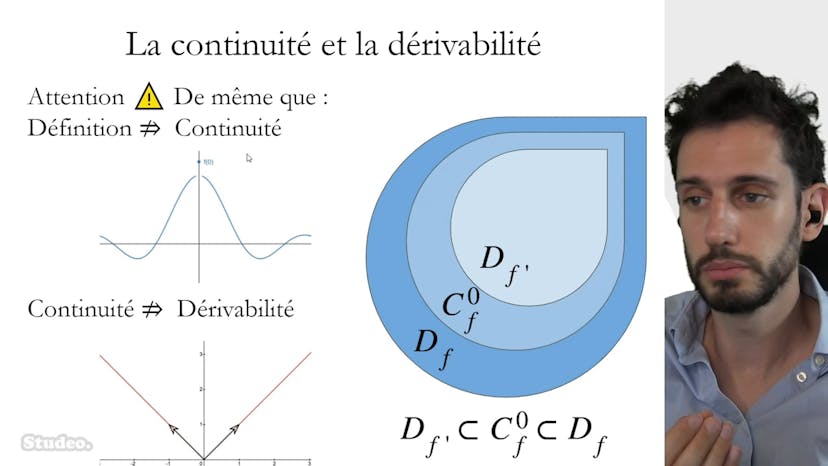
Continuité vs dérivabilité
Ce cours explique le lien entre dérivabilité et continuité. Si une fonction est dérivable en un point, alors elle est continue en ce point, mais le contraire n'est pas vrai. La démonstration utilise la limite de la fonction et le taux d'accroissement en ce point pour arriver à la définition de la continuité. L'ensemble des réels où la fonction est définie est plus grand que l'ensemble où elle est continue et l'ensemble où elle est dérivable est contenu dans l'ensemble où elle est continue. Deux exemples de fonctions continues mais non dérivables sont la racine carrée en zéro et la valeur absolue.
Maths Spé
Analyse
Terminale

Continuité et suites : Théorème du point fixe
Le théorème du point fixe est un résultat important en mathématiques qui s'applique à l'étude des suites. Il dit que si une fonction continue f sur un intervalle i a un point fixe l tel que f(l)=l, alors toute suite définie récursivement par un+1=f(un) converge vers ce point fixe l. Cependant, il est important de noter que la continuité de la fonction est nécessaire pour que ce théorème fonctionne. Enfin, il existe différents types de convergence possibles pour les suites définies de manière récurrente, en fonction de la courbure de la fonction.
Maths Spé
Analyse
Terminale
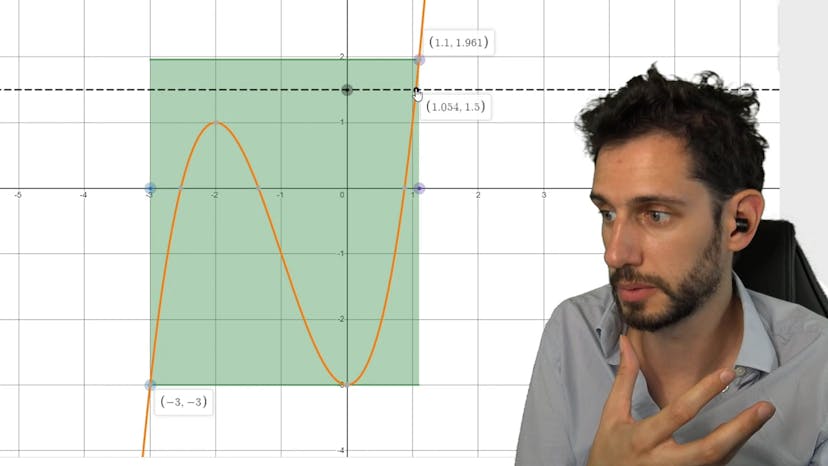
TVI : LE théorème
Le théorème des valeurs intermédiaires est capital en continuité et est utile pour les études de fonctions et la résolution d'équations. En bref, si f est une fonction continue sur un intervalle a, b pour tout réel k compris entre f2a et f2b, l'équation f2x égale k admet au moins une solution c dans l'intervalle a, b. Lorsque la fonction trace des zigouigouis, les valeurs de k peuvent croiser la fonction plusieurs fois, mais lorsque la fonction est strictement croissante ou décroissante, elle ne croisera la valeur de k qu'une seule fois. Il est important de citer le théorème des valeurs intermédiaires pour justifier son utilisation et pour identifier les solutions pour chaque intervalle où la fonction est bijective ou strictement croissante/décroissante. Le théorème de la bijection est un autre nom pour le théorème des valeurs intermédiaires, mais uniquement pour les cas de strictes croissances ou décroissances.


