Cours d'apprentissage en ligne

Équation y'=ay+φ

Dans ce cours, nous apprenons comment résoudre une équation différentielle de la forme y' = y + phi. Comparé à l'équation y' = y + b, la différence entre b et phi est que b est une constante tandis que phi est une fonction qui peut varier. Cela rend la résolution un peu plus complexe pour trouver la solution particulière. La méthode générale de résolution reste la même : nous devons d'abord trouver une solution particulière en résolvant l'équation sans l'équation homogène (y' = y), puis nous ajoutons la solution homogène. La différence ici est que nous ne cherchons pas une solution particulière sous forme constante. Pour cela, nous avons besoin d'un petit indice fourni dans l'énoncé. Dans cet exemple, on nous demande de vérifier que la fonction p(x) est une solution de l'équation 2. Nous prenons p(x) comme un polynôme, calculons sa dérivée et vérifions si 2p'(x) + 6p(x) est égal à x^2 + 2x - 1. Après les calculs, nous constatons que p(x) est bien une solution. Ensuite, on nous demande de montrer que si f est une solution de l'équation E, cela équivaut à dire que f - p est une solution de l'équation E'. Nous remplaçons x^2 + 2x - 1 par 2p'(x) + 6p(x) dans l'équation pour montrer cette équivalence. En factorisant, nous obtenons 2f'(x) - 2p'(x) + 6f(x) - 6p(x) = 0. De là, nous obtenons que f - p est une solution de l'équation E', où E' est l'équation homogène. Nous résolvons ensuite l'équation E', qui est une équation différentielle que nous connaissons bien : linéaire à coefficient constant de premier ordre sans seconde membre. Nous l'isolons pour obtenir Y' = -3y et reconnaissons une forme de type Y' = Y avec A = -3. En utilisant ce que nous avons dit précédemment sur f - p, nous isolons f sous la forme A*e^(-3x) + p(x). Finalement, nous trouvons que f est de la forme A*e^(-3x) + (1/6)*x^2 + (2/9)*x - 13/54. Nous remarquons qu'il y a toujours une constante de multiplication inconnue. Pour la trouver, nous aurions besoin de conditions particulières dans la fonction, que nous ne possédons pas ici. Cependant, nous pouvons conclure que les fonctions de la forme A*e^(-3x) + (1/6)*x^2 + (2/9)*x - 13/54 sont toutes des solutions de l'équation différentielle. Cela résume le cours sur la résolution des équations différentielles du type y' = y + phi, où phi est une fonction non constante.

Second membre en exponentielle

Les équations différentielles sont importantes dans les études d'ingénieur. Pour une équation du premier ordre du type Y' + Ay = Phi(X), la solution se divise en deux parties. La première partie est la solution sans second membre, qui est généralement l'exponentielle de -AX. La deuxième partie est la solution particulière, qui dépend de la nature de Phi(X). Par exemple, si Phi(X) est une fonction X^2, la solution sera une fonction en X^2. Si Phi(X) est exponentielle 8X, la solution particulière sera de la forme K * exponentielle 8X. Si Phi(X) est une somme de termes, on peut séparer la solution en plusieurs problèmes. Par exemple, si on a X^2 + log(X), on peut trouver une solution sans second membre pour X^2 et une solution sans second membre pour log(X). En résumé, pour résoudre une équation différentielle du premier ordre, on cherche d'abord une solution sans second membre et une solution particulière en fonction de la nature de Phi(X). Ensuite, on peut combiner ces solutions pour obtenir l'ensemble des solutions possibles.

Solution particulière : trigonométrie

Dans ce cours, nous examinons l'équation différentielle donnée et cherchons une solution particulière. Une forme possible est suggérée, mais après une tentative infructueuse, nous réalisons qu'il est préférable d'utiliser à la fois le cos et le sin. Nous identifions ensuite les termes en cos et en sin dans l'équation pour obtenir 0 sin, moins un cinquième cos x et plus deux cinquièmes sin x. En utilisant ces termes, nous formons l'expression y' - 1/2 y = 1/2 cos x. Ainsi, la solution générale de l'équation différentielle est donnée par y(x) = (1/2)e^(x/2)K + g(x), où K est une constante et g(x) est une fonction quelconque. Cette solution générale est obtenue en combinant la solution particulière et la solution sans second membre de l'équation. En conclusion, le principe de résolution des équations différentielles est appliqué, avec une difficulté accrue lors de la recherche de la solution particulière dans des exercices plus avancés.

Solution particulière plus difficile

Dans ce cours, nous examinons comment résoudre l'équation différentielle y'-2y = xe^2x de manière SEO conviviale. Nous commençons par observer que l'expression xe^2x ressemble à un produit entre x et e^2x. Nous essayons donc de trouver une solution particulière de la forme ax + b. Cependant, nous réalisons que cette tentative peut échouer car l'expression ne correspond pas exactement à ce que nous avons identifié. Ensuite, nous envisageons une autre possibilité en utilisant une fonction quadratique g(x) = ax^2 + bx + c. Si notre tentative précédente a échoué, nous essayons cette fois-ci une fonction quadratique. Nous expliquons pourquoi cela peut être nécessaire en utilisant notre expérience : lorsque l'équation à résoudre est égale à zéro et a une solution du type e^2x, nous constatons que généralement, nous devons augmenter le degré de la fonction pour trouver une solution. C'est pourquoi nous ne pouvons pas trouver une fonction g(x) qui satisferait l'équation. Nous encourageons les étudiants à ne pas paniquer lorsqu'ils sont confrontés à ce genre de situation. L'étape suivante consiste simplement à réessayer avec une fonction polynomiale de degré 2. Dans notre cas, nous choisissons g(x) = ax^2 + bx + c et constatons que certains termes disparaissent lors de la résolution. Cela est facilement compréhensible si l'on se rappelle que le terme x^2 dans g(x) disparaissait lors de la tentative précédente avec une fonction plus simple. La valeur de c n'affecte pas la solution, nous choisissons donc c = 0 pour simplifier nos calculs. Ainsi, nous trouvons une solution g(x) qui est approximativement de degré 2 fois l'exponentielle de 2x. La solution générale est alors donnée par y(x) = k*e^(2x) + (x^2/2)*e^(2x), où k est une constante réelle qui variera en fonction des conditions initiales. En forme réduite, nous avons y(x) = (k + x^2/2)*e^(2x). Il est important de noter que la forme réduite de la solution permet une interprétation plus intuitive des termes constants et exponentiels. Veillez également à adapter cette solution en fonction du contexte et des conditions initiales spécifiques.

Introduction

Dans cette vidéo d'introduction sur les intégrales, nous allons présenter les définitions et les propriétés de l'intégrale. Tout au long du chapitre, nous allons calculer des R sous des courbes. Dans ce sous-chapitre, nous posons les bases pour les fonctions continues et nous examinons les fonctions positives et négatives. Nous commençons par un exemple simple. Si nous avons une fonction constante avec une hauteur de 2 et une plage de 0 à 3, l'R sous la courbe est égal à 6, ce qui est représenté par un rectangle de largeur 3 et de hauteur 2. Nous pouvons faire la même chose avec une fonction affine de pente 1, qui est représentée par un triangle rectangle isocèle avec une base de 3 et une hauteur de 3. L'R est donc égal à 9 demi (9/2). Vous pourriez vous demander pourquoi consacrer un chapitre à cela. En réalité, nous aurons des fonctions plus complexes et nous utiliserons cette approximation simple du rectangle pour comprendre comment fonctionne l'R sous une fonction plus courbe et complexe. Ainsi, nous pourrons dire que cela équivaut à l'R d'une somme de rectangles, du moins approximativement. Les rectangles auront une largeur (delta x) et une hauteur (f de x) en fonction du point considéré. Pour être plus précis, ce symbole "S" stylisé représente une somme entre a et b. L'R est essentiellement égal à la somme des rectangles lorsque le nombre de rectangles devient infini, c'est-à-dire lorsque la somme atteint une R complète plutôt qu'une approximation. Nous utilisons également la notation "dx" pour représenter une largeur infiniment petite lorsque le nombre de rectangles devient très grand. Dans ce sous-chapitre, nous allons aborder les définitions de l'intégrale pour les fonctions continues positives et les fonctions de signes quelconques. Nous utiliserons des encadrements et des intuitions graphiques pour estimer les intégrales. Les méthodes abordées seront le calcul de l'R et l'estimation de l'intégrale à l'aide de rectangles. Bon courage pour ce chapitre, et je vous retrouve dans la prochaine vidéo. N'hésitez pas à poser vos questions dans la FAQ, et à bientôt !

Définition de l'intégrale

L'intégrale d'une fonction continue et positive sur un intervalle a, b correspond à l'aire sous la courbe de cette fonction entre les valeurs a et b, ainsi que l'axe horizontal. On peut également l'appeler le domaine sous la courbe ou l'aire sous la courbe. L'unité utilisée pour mesurer cette aire est l'unité d'air, qui est un petit carré de taille 1 sur 1 dans un repère orthonormé. On note l'intégrale comme une expression mystérieuse "intégrale entre a et b de f de x, dx". Cette définition peut être étendue aux fonctions négatives en calculant la surface correspondante et en lui attribuant un signe négatif. Dans certains cas, il peut y avoir des parties positives et des parties négatives de la fonction. Il est important de se rappeler que l'intégrale est positive lorsque la fonction est au-dessus de l'axe OX et négative lorsqu'elle est en dessous. N'hésitez pas à poser des questions supplémentaires dans la FAQ.

Encadrement et intuition graphique

Dans cette vidéo, nous abordons différentes méthodes d'approximation de l'aire sous une courbe. Nous commençons par expliquer que lorsque la courbe est une droite, le calcul de l'aire est assez simple, en utilisant des formes géométriques comme des triangles ou des rectangles. Cependant, lorsque la courbe est incurvée, il devient plus compliqué de calculer l'aire. Nous présentons donc les méthodes d'approximation suivantes : les rectangles supérieurs et inférieurs. Ces méthodes consistent à diviser l'intervalle en plusieurs petits intervalles de même amplitude, et à construire des rectangles inférieurs qui collent la courbe par en dessous, ainsi que des rectangles supérieurs qui collent la courbe par en dessus. Lorsque le nombre de rectangles tend vers l'infini et que leur taille diminue, les rectangles inférieurs et supérieurs convergent vers la vraie valeur de l'aire. En plus de ces méthodes, nous mentionnons brièvement d'autres méthodes qui ne sont pas au programme, mais qui illustrent différentes possibilités : la méthode du point milieu et la méthode des trapèzes. La méthode du point milieu consiste à tracer des rectangles qui sont traversés par la courbe au milieu de leur côté supérieur, offrant ainsi une meilleure précision. La méthode des trapèzes permet quant à elle d'utiliser des quadrilatères non-rectangulaires, offrant ainsi plus de liberté pour se rapprocher de la courbe. En conclusion, cette vidéo explicative présente les différentes méthodes d'approximation de l'aire sous une courbe, en mettant notamment l'accent sur les rectangles supérieurs et inférieurs.

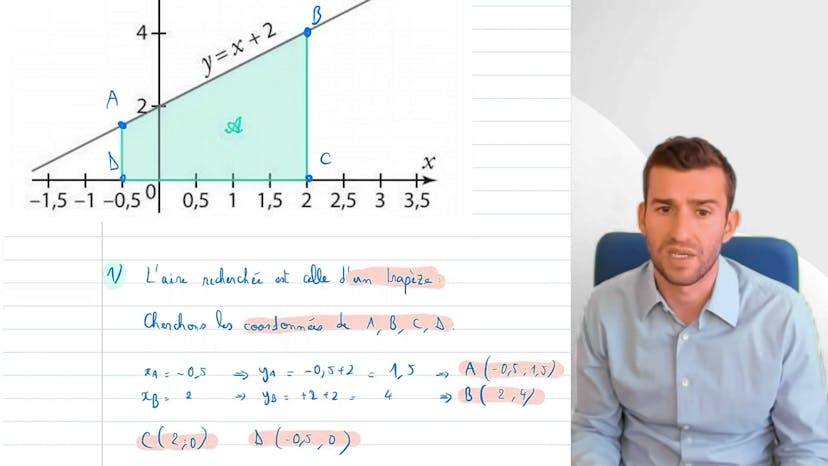
Intégrale et Aire

Lors de ce cours, nous apprenons comment calculer une intégrale de manière géométrique sans utiliser la fonction. Cela est possible lorsque la forme géométrique est simple, comme dans notre exemple avec une fonction affine. Nous nous intéressons à l'intégrale de la fonction x plus 2 entre -0,5 et 2. Pour calculer cette intégrale, nous pouvons utiliser deux méthodes : calculer la primitive de x plus 2, ce qui est relativement simple, ou utiliser une forme géométrique connue pour calculer facilement l'erreur. Dans ce cas, la forme géométrique est un trapèze, ce qui facilite le calcul. Pour cela, nous avons besoin de la hauteur, de la largeur et de la longueur des bases du trapèze. Nous trouvons les coordonnées des points a, b, c et d en utilisant les équations de la droite. Les coordonnées de a sont (-0,5, 1,5) et les coordonnées de b sont (2, 4). Les points c et d étant sur l'axe des abscisses, leurs coordonnées sont (2, 0) et (-0,5, 0) respectivement. Nous calculons ensuite les différentes longueurs du trapèze en prenant la différence entre les ordonnées des deux points correspondants. Cela donne 1,5 pour la longueur a-d, 4 pour la longueur b-c et 2,5 pour la longueur d-c. En appliquant la formule de l'aire du trapèze, qui est la moyenne des deux bases multipliée par la hauteur, nous obtenons l'aire du trapèze. Dans notre cas, cela donne 1,5 * (1,5 + 4) * 2,5, soit 6,875. Cette méthode permet de calculer une intégrale en utilisant directement l'aire géométrique du trapèze, sans avoir besoin de calculer les primitives. Il suffit de trouver les coordonnées des points et de calculer les longueurs et l'aire du trapèze. Cela conclut notre méthode de calcul d'une intégrale à l'aide d'une forme géométrique.

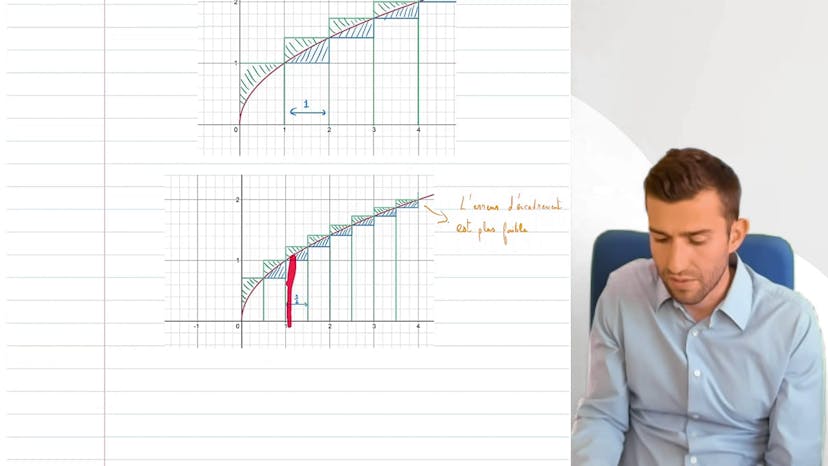
Méthode des Rectangles

Dans ce cours, nous apprenons à calculer une aire géométrique à l'aide de la méthode des rectangles. La courbe intégrée n'a pas une forme géométrique simple, donc nous ne pouvons pas calculer l'aire de manière directe. Cependant, nous pouvons encadrer cette aire en utilisant des petits rectangles en dessous de la courbe et des grands rectangles au-dessus. En diminuant la largeur des rectangles, nous affinons notre encadrement et nous tendons vers l'aire recherchée, c'est-à-dire l'intégrale. Nous cherchons donc à encadrer l'aire sous la courbe de la fonction de 0 à 4. La fonction est croissante, donc nous encadrons l'aire en utilisant les rectangles a'0, a'1, a'2 et a'3. Les a'0, a'1, a'2 et a'3 se calculent en multipliant la largeur par la hauteur de chaque rectangle. Par exemple, a'1 est égal à 1 fois 1 (largeur fois hauteur), ce qui donne 1. En utilisant ces calculs, nous obtenons l'encadrement 1 plus racine de 2 plus racine de 3 pour l'aire sous la courbe, et 3 plus racine de 2 plus racine de 3 pour l'encadrement formé par les petits rectangles. Pour augmenter la précision de l'encadrement, nous pouvons utiliser des rectangles de largeur plus petite, comme 1,5, 1,25, etc. En faisant tendre la largeur vers zéro, nous obtenons des rectangles qui collent de plus en plus à la courbe et ainsi un encadrement plus précis. En résumé, la méthode des rectangles permet d'encadrer l'intégrale lorsque nous ne pouvons pas trouver une primitive de la fonction. Il est possible d'améliorer la précision de l'encadrement en utilisant des rectangles de plus en plus petits.

Introduction

Ce cours introduit un nouveau sous-chapitre sur les intégrales et leur lien avec les primitives. Il explique que ce sous-chapitre est assez théorique et demande de la concentration. L'objectif est de trouver des méthodes exactes pour calculer les intégrales, au lieu d'utiliser des approximations. On découvre qu'il existe un lien exact entre le calcul des intégrales et les primitives. Cela permet de calculer les intégrales de manière exacte, ce qui est très intéressant. Ce lien fonctionne dans les deux sens, ce qui permet de calculer les intégrales en utilisant les primitives, mais aussi de trouver des primitives pour des fonctions qui ne sont pas calculables avec des fonctions usuelles. On mentionne également quelques propriétés générales des intégrales, qui sont utiles pour les physiciens et les mathématiciens. Le cours se termine en présentant les points clés du chapitre, notamment le théorème fondamental, la condition suffisante d'existence d'une primitive et des méthodes de calcul des intégrales. L'enseignant encourage les étudiants à poser des questions dans la FAQ et annonce la prochaine vidéo.

Théorème fondamental : énoncé

Le théorème fondamental de l'analyse établit un lien entre la notion de primitive et l'intégrale d'une fonction continue et positive sur un intervalle donné. Selon ce théorème, si f est une telle fonction, alors la fonction F définie comme l'intégrale de f entre les points a et x est dérivable, et sa dérivée est égale à f elle-même. Ainsi, F est une primitive de f. Ce lien peut être visualisé à l'aide d'un graphique représentant une fonction parabole (x²) avec un signe négatif. En calculant l'aire sous la courbe, on constate que celle-ci varie en fonction des valeurs positives et négatives de la fonction. Plus précisément, l'aire augmente lorsque la fonction est négative et diminue lorsqu'elle est positive. Si la fonction est croissante, l'aire augmente rapidement, tandis que si elle est décroissante, l'aire diminue lentement. Lorsque la fonction atteint zéro, l'aire totale est également de zéro. Grâce à cette visualisation, il apparaît que la fonction bleue tracée sur le graphique, qui ressemble à une fonction cubique, présente des caractéristiques similaires à celles de la fonction verte (la fonction dérivée). En effet, la fonction bleue décroît lorsque la fonction verte est négative et croît lorsque la fonction verte est positive. Cela suggère que la fonction bleue peut être une primitive de la fonction verte. Cette visualisation peut être utile pour comprendre le lien entre la primitive d'une fonction et l'aire sous sa courbe. La démonstration formelle de ce lien sera présentée dans une vidéo ultérieure.