Cours d'apprentissage en ligne

Autre dépendance en n

Dans cet exercice, nous devons déterminer le PGCD de deux entiers, a et b, en fonction de la valeur de n. Pour simplifier le calcul, nous souhaitons éliminer la variable n et nous concentrer uniquement sur le PGCD. Nous utilisons donc une combinaison linéaire de a et b pour éliminer n, ce qui nous donne l'équation 3a-b. Comme le PGCD de a et b divise cette combinaison linéaire, il divise également le nombre 5. Étant donné que 5 est un nombre premier, cela signifie que le PGCD ne peut être que 1 ou 5. Nous examinons ensuite ces deux cas séparément pour déterminer les valeurs possibles de n. Si le PGCD est égal à 5, cela signifie que a est divisible par 5 (congru à 0 modulo 5). En utilisant l'expression de a (n+4), nous constatons que n doit être congru à 1 modulo 5 pour satisfaire cette condition. D'autre part, si le PGCD est égal à 1, cela signifie que n n'est pas congru à 1 modulo 5. En conclusion, le PGCD de a et b est égal à 5 si et seulement si n est congru à 1 modulo 5, et il est égal à 1 si et seulement si n n'est pas congru à 1 modulo 5.

PGCD et n carré

Aucun résumé n'est disponible pour cette vidéo

PGCD et PPCM

Dans cet exercice, nous devons trouver deux nombres en utilisant le PGCD (Plus Grand Commun Diviseur) et le PPCM (Plus Petit Commun Multiple). Les informations que nous avons sont que A est plus petit que B, et que leur PGCD est égal à 6 et leur PPCM est égal à 102. Nous pouvons utiliser une formule qui relie ces nombres : le produit de deux nombres est égal au produit de leur PGCD et de leur PPCM. Nous pouvons donc utiliser une propriété du PGCD pour trouver A' et B', tels que A = 6*A' et B = 6*B', et A' et B' sont premiers entre eux. En écrivant cette formule avec les valeurs de A et B, nous obtenons 6*A'*6*B' = 6*102. Nous simplifions en divisant par 6 et en remarquant que 102 = 6*17, nous obtenons A'*B' = 17. Nous savons que A' et B' sont premiers entre eux et que leur produit vaut 17, qui est un nombre premier. Sachant que A' est plus petit que B', nous pouvons conclure que A' = 1 et B' = 17. Maintenant, nous pouvons trouver A et B en utilisant les équations A = 6*A' et B = 6*B'. Donc, A = 6*1 = 6 et B = 6*17 = 102. Ainsi, A = 6 et B = 102 sont les deux nombres recherchés.

PGCD et congruences

Dans cet exercice, nous devons montrer une équivalence entre deux systèmes de congruence. Le premier système stipule que 'n' est congruent à 1 modulo 5 et congruent à 5 modulo 7. Pour prouver cela, nous examinons les deux lignes du système. Dans la première ligne, nous remarquons que si 'n' est congruent à 1 modulo 5, alors 4n + 1 est congruent à 0 modulo 5. Dans la deuxième ligne, si 'n' est congruent à 5 modulo 7, alors 4n + 1 est congruent à 0 modulo 7. En utilisant le corollaire du théorème de Gauss, qui stipule que si deux nombres A et B sont premiers entre eux et divisent un nombre C, leur produit AB divise également C, nous concluons que 5 et 7 étant premiers entre eux, leur produit divise 4n + 1. Ainsi, nous obtenons que 4n + 1 est congruent à 0 modulo 35. Pour résoudre ce système, nous cherchons à isoler 'n'. En utilisant une méthode spécifique pour résoudre des équations de la forme AX congruent à B modulo n, nous trouvons un entier k tel que 4k est congruent à 1 modulo 35. En multipliant les deux côtés de l'équation par k, nous obtenons que 'n' est congruent à 26 modulo 35. Les solutions de ce système sont donc tous les nombres de la forme 26 + 35k, avec k appartenant à Z.

PGCD et Suite

Dans cet exercice, nous étudions une suite définie par récurrence et nous cherchons à montrer qu'elle est une suite géométrique. La première suite, notée un, est donnée par u0=0, u1=1, et un+2=3un+1-2un. La deuxième suite, notée vn, est définie comme vn=un+1-un. Nous devons déterminer la raison et le premier terme de la suite géométrique vn. Pour montrer que vn est une suite géométrique, nous calculons vn+1 et essayons de l'écrire sous la forme d'un multiple de vn. En utilisant la relation de récurrence pour un, nous obtenons vn+1=2vn. Ainsi, nous avons démontré que vn est une suite géométrique de raison 2 et que le premier terme v0 est égal à 1. Ensuite, nous devons déduire que pour tout entier n, un+1=2(un+1). Cette question peut sembler étrange car elle concerne la suite vn dont nous venons de montrer qu'elle est géométrique. Cependant, il faut remarquer que vn est construite de manière particulière. En fait, vn est la différence entre deux termes consécutifs de la suite un. Nous pouvons alors utiliser une somme télescopique pour trouver une relation entre un et un+1. En effectuant cette somme, nous obtenons un+1=2(un+1). Ainsi, nous avons prouvé que pour tout entier n, un+1 est égal à 2(un+1). Enfin, nous devons déduire que deux termes consécutifs de la suite un sont premiers entre eux. Pour cela, nous utilisons le théorème de Bézout, qui stipule qu'une combinaison linéaire de deux entiers est égale à leur PGCD (Plus Grand Commun Diviseur). En utilisant l'égalité un+1=un+1-2un, nous obtenons que le PGCD de un et un+1 est égal à un. Par conséquent, deux termes consécutifs de la suite un sont bien premiers entre eux.

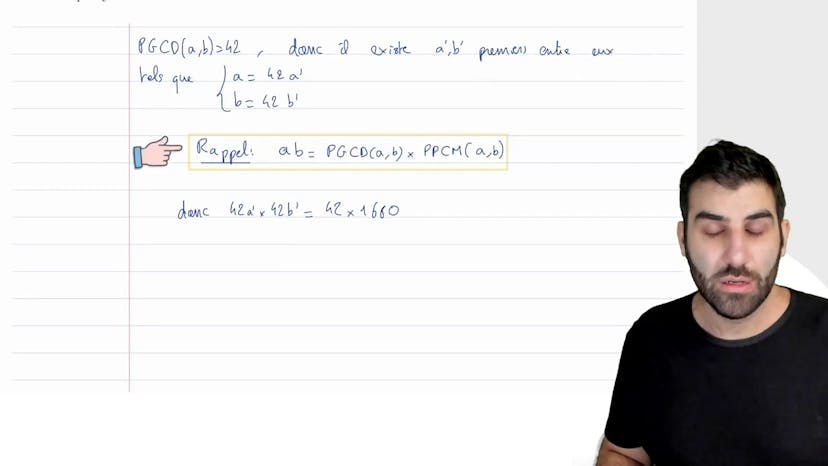
PGCD+PPCM

Dans cet exercice, nous cherchons un couple A et B dont le PGCD est égal à 42 et le PPCM est égal à 1680. Pour résoudre ce problème, nous utilisons la méthode d'extraction des diviseurs premiers de A et de B. Étant donné que le PGCD des deux nombres est égal à 42, nous pouvons les représenter comme suit : A = 42A' et B = 42B', où A' et B' sont premiers entre eux. En utilisant la formule selon laquelle le produit de deux nombres est égal au produit de leur PGCD et de leur PPCM, nous pouvons simplifier l'expression. Ainsi, nous obtenons A' B' = 40. En excluant les diviseurs de 40 qui ne sont pas premiers entre eux, nous identifions les seules possibilités pour A' et B', qui sont 1 et 40, ainsi que 5 et 8. En supposant que A est plus petit que B, nous en déduisons les possibilités pour A et B, qui sont A = 42 et B = 1680, ou A = 210 et B = 336. Ce sont donc toutes les solutions possibles de ce système d'équations basé sur le PGCD et le PPCM.

test

Aucun résumé n'est disponible pour cette vidéo

Nombres premiers entre eux

Dans cet exercice, nous voulons déterminer si 59 et 27 sont premiers entre eux. Deux nombres sont premiers entre eux s'ils n'ont aucun diviseur en commun. Pour vérifier cela, nous pouvons décomposer chaque nombre en facteurs premiers et vérifier s'il y a un nombre premier commun dans cette décomposition. Pour commencer, nous décomposons 27 en facteurs premiers et obtenons 3 puissance 3, ce qui signifie que le seul nombre premier dans sa décomposition est 3. Cela signifie que s'ils ont un diviseur commun différent de 1, ce sera un multiple de 3. Cependant, 3 ne divise pas 59. Pour confirmer cela, nous utilisons un critère de divisibilité qui consiste à additionner les chiffres d'un nombre et vérifier si le résultat est divisible par 3. Lorsque nous additionnons 5 et 9, nous obtenons 14, qui n'est pas divisible par 3. Par conséquent, 59 n'est pas divisible par 3. En conclusion, le plus grand commun diviseur (PGCD) de 59 et 27 est égal à 1, ce qui signifie que ces deux nombres sont premiers entre eux.

Équation diophantienne

Dans cet exercice, nous cherchons à résoudre l'équation diophantienne 13x + 9y = 2. Pour résoudre ce type d'équation, nous devons trouver une solution particulière et ensuite généraliser les solutions en utilisant les coefficients. Afin de trouver une solution particulière, nous utilisons l'algorithme de Clyde pour trouver le PGCD. Ici, le PGCD de 9 et 13 est 1, ce qui divise bien le nombre 2. Donc l'équation admet des solutions entières. Ensuite, nous trouvons une solution particulière en utilisant la relation de Bézout, qui est 1 = 13 (-4) + 9 (6). Pour obtenir une solution correspondant à 2, nous multiplions simplement cette équation par 2, ce qui nous donne 2 = 13 (-8) + 9 (12). Ainsi, nous avons une solution particulière qui est (-8, 12). Maintenant, nous déterminons l'ensemble des solutions en utilisant les coefficients. Pour x, nous ajoutons le coefficient devant y (9) et le multiplions par un paramètre k, ce qui donne x = -8 + 9k. Pour y, nous soustrayons le coefficient devant x (13) et le multiplions également par un paramètre k, ce qui donne y = 12 - 13k. Donc, l'ensemble des solutions de cette équation est donné par les paires de valeurs (x, y) telles que x = -8 + 9k et y = 12 - 13k.

Fraction irréductible

Dans cet exercice, nous souhaitons démontrer que la fraction (9n + 1) / (6n + 1) est irréductible pour tout entier n. Pour commencer, rappelons que pour qu'une fraction soit irréductible, il faut que le PGCD (Plus Grand Commun Diviseur) du numérateur et du dénominateur soit égal à 1. Nous rappelons également le théorème de Bézout, qui énonce que le PGCD de deux nombres est égal à 1 si et seulement si il existe des entiers u et v tels que a*u + b*v = 1. En utilisant ces rappels, nous pouvons dire que la fraction est irréductible si et seulement si il existe des entiers u et v tels que (9n + 1)*u + (6n + 1)*v = 1. En développant cette équation, nous obtenons n*(9u + 6v) + u + v = 1. Pour que cette équation soit vraie pour tout n, il faut nécessairement que n*(9u + 6v) + u + v = 0. En résolvant les deux équations simultanément, nous trouvons u = -2 et v = 3. Donc nous avons trouvé des entiers u et v qui vérifient l'équation, et ils sont premiers entre eux. Ainsi, nous pouvons conclure que (9n + 1) / (6n + 1) est une fraction irréductible pour tout entier n, selon le théorème de Bézout.

Système congruences et Bezout

Cet exercice consiste à résoudre un système de congruences en utilisant les équations de Dioff-Ancienne. Le système à résoudre est le suivant : x congru à 1 modulo 11, et x congru à 3 modulo 4. Pour montrer que ce système revient à résoudre l'équation 11u + 4v = 2, où u et v sont des entiers relatifs, on écrit les équations de congruence en notation algebrique. On obtient x = 1 + 11u et x = 3 + 4v. En simplifiant, on obtient l'équation 11u - 4v = 2, ce qui est l'équation diophantienne recherchée. On vérifie si cette équation a des solutions en utilisant le PGCD de 11 et 4, qui est égal à 1. Comme 1 divise 2, l'équation a des solutions. On trouve une solution particulière en observant que 11 et 4 ont des multiples qui se comportent bien ensemble, comme 12. On obtient les coefficients de Bézout en prenant -1 pour u et -3 pour v. En multipliant ces coefficients par 2, on obtient une solution particulière de l'équation, soit u = -2 et v = -6. On généralise ensuite les solutions en ajoutant un coefficient k à la solution particulière. Finalement, on simplifie en remplaçant les coefficients négatifs par des coefficients positifs, et on obtient que u = 2 + 4k et v = 5 + 11k sont les solutions de l'équation diophantienne. Pour trouver les solutions du système initial, on remplace u et v dans les équations de congruence. On obtient x = 23 + 44k, ce qui signifie que les solutions du système sont congrues à 23 modulo 44.