 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc

Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Maths SM&SP
Analyse
2BAC SM Maroc

Introduction Limites
Lorsqu'on étudie les limites de fonctions, on peut s'inspirer de ce qu'on a vu sur les suites. Les suites sont des fonctions qui portent uniquement sur les entiers, tandis que les fonctions sont plus génériques et se portent sur l'ensemble des réels. Ainsi, on peut parler de limites en l'infini et en un réel. Il y a aussi des cas où il n'y a pas de limite, par exemple lorsque la fonction oscille à l'infini. Dans le cas où la limite existe, la fonction peut se rapprocher d'une valeur réelle ou tendre vers plus ou moins l'infini. On peut illustrer ces cas avec des graphes. Dans cette vidéo d'introduction, nous aborderons ces différents cas et introduirons la notion d'asymptote. En résumé, il faut connaître les définitions et les exemples de limites, ainsi que les méthodes d'analyse graphique et de calcul des limites. N'hésitez pas à poser des questions et interagir avec les autres membres dans la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

En l'infini, limites finies et infinies
Il est important de comprendre les concepts de limites pour x tendant vers l'infini en mathématiques. Pour cela, nous devons connaître deux définitions : lorsque x tend vers l'infini et lorsque x tend vers un réel L.
Lorsque x tend vers l'infini, cela signifie que peu importe le plateau Y que nous choisissons, la fonction finira toujours par dépasser complètement ce plateau.
Lorsque x tend vers un réel L, cela signifie que toutes les valeurs de la fonction finiront toujours par être dans un couloir autour de la limite L. Peu importe la largeur du couloir, la fonction sera toujours comprise à l'intérieur.
Il est important de préciser si x tend vers l'infini ou vers un réel L dans la notation mathématique.
Ces concepts de limites pour x tendant vers l'infini sont similaires à ceux que nous avons vus dans les suites en mathématiques.
Il est conseillé de bien comprendre ces définitions et de les utiliser correctement dans les exercices, car cela peut être un point facile à perdre ou à gagner.
N'hésitez pas à poser des questions si vous avez des doutes, et nous vous retrouverons dans la prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc
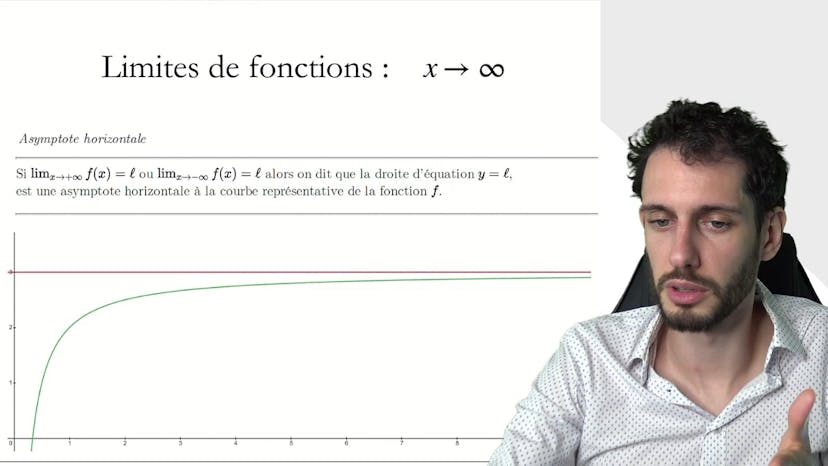
Les asymptotes horizontales
Dans cette vidéo, nous abordons le concept d'asymptote horizontale qui se produit lorsque la limite de la fonction F tend vers un nombre réel lorsque X devient extrêmement grand. Une asymptote horizontale est une droite vers laquelle la courbe de F tend à se rapprocher. Il est important de noter que l'asymptote est une droite à laquelle la courbe de F se colle, et non pas à la fonction F elle-même. On peut donner l'exemple de la fonction 1/X où 3 est la limite de la fonction. La droite Y=3 est asymptote à la courbe de F car elle se colle à cette dernière. On peut également observer des asymptotes du côté gauche de l'axe des X lorsque nous nous approchons de moins l'infini. Un autre exemple d'asymptote intéressant est le sinus qui, lorsqu'il est comprimé, se rapproche d'une droite asymptote. La définition d'une asymptote est une droite vers laquelle la courbe de F se colle et se rapproche infiniment. Ce concept d'asymptote horizontale est intuitivement lié à la notion de limite. N'hésitez pas à poser des questions dans la FAQ et je vous retrouve pour la prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc
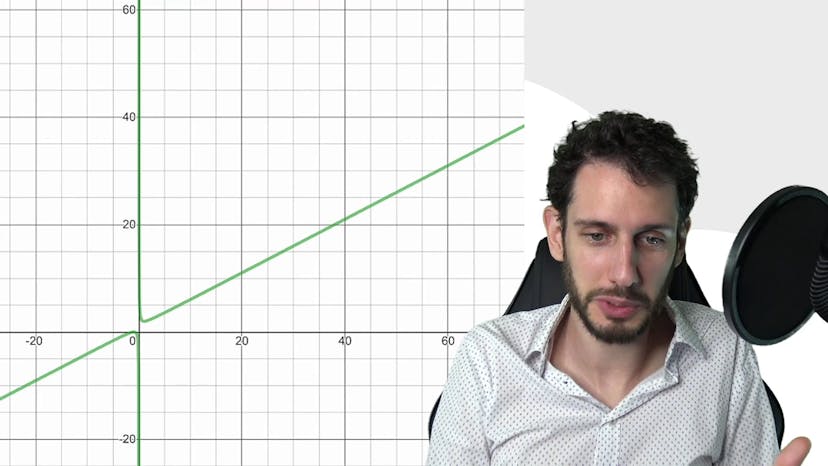
Bonus : Les asymptotes obliques
Dans cette vidéo, nous abordons le concept d'asymptote oblique, qui se produit lorsque l'asymptote n'est plus horizontale mais a une pente spécifique. Pour une fonction f définie sur un ensemble de définitions, la courbe cf est la représentation graphique de la fonction. Lorsque la différence entre f2x (la valeur de f2x) et ax plus b (une droite affine) tend vers 0 à mesure que x approche l'infini ou moins l'infini, cela signifie que la courbe se rapproche de la droite ax plus b. Ce cas se produit fréquemment dans les exercices de mathématiques, il est donc important de le comprendre et de le détecter. Un exemple simple est présenté, où la fonction verte se rapproche de plus en plus d'une droite rouge lorsque x approche l'infini. Cela est illustré graphiquement en zoomant et en observant que la fonction devient presque indiscernable de la droite affine. Cette vidéo vise à illustrer le concept d'asymptote oblique, et d'autres concepts tels que les asymptotes verticales seront abordés dans une vidéo ultérieure.
Maths SM&SP
Analyse
2BAC SM Maroc

En un point réel, limite infinie
Lorsque nous parlons des limites de fonctions avec x tendant vers un réel a, nous avons deux cas principaux. Dans le premier cas, la fonction F tend vers l'infini ou moins l'infini. Dans le deuxième cas, la fonction F converge vers une valeur finie. Nous nous concentrerons d'abord sur ce deuxième cas, qui est plus simple mais aussi un peu bizarre.
L'idée est que lorsque x se rapproche de a, la courbe de la fonction suit son cours normal et nous amène à différents points. Cela correspond à la notion de continuité, que nous étudierons plus en détail ultérieurement. Par exemple, si nous prenons la limite de x + 3 lorsque x tend vers 2, nous obtenons simplement 2 + 3, soit 5.
Cependant, il existe des cas plus complexes, comme la limite de sin(x)/x lorsque x tend vers 0. Il s'agit d'un cas bizarre car cela donne 0/0, ce qui n'est pas évident à évaluer. Pour éviter cette division par 0, nous choisissons de définir la fonction sin(x)/x sur R* (l'ensemble des réels à l'exception de 0). Dans ce cas, il est possible de démontrer que la limite vaut 1.
Sur un graphe, nous pouvons voir que la fonction sin(x)/x encadre le point (0,1) avec deux branches qui se rapprochent de ce point. Cela montre qu'il s'agit bien d'une limite où x tend vers 0 et la fonction converge vers 1.
En ce qui concerne les limites infinies, nous utilisons la notion de plateau qui bloque la fonction. Pour pouvoir dépasser n'importe quel plateau, nous utilisons la définition suivante : F tend vers plus l'infini si F est indépassable par un plateau. Par exemple, pour une hyperbole, nous constatons que peu importe la taille du plateau, la fonction finira par le dépasser. Cela définit la notion de tendeur plus infini.
Finalement, nous introduisons la notion d'asymptote verticale, qui est une droite à laquelle la fonction se colle lorsque x tend vers plus ou moins l'infini et a une limite plus l'infini en un point fini. Par exemple, lorsque la limite à gauche ou à droite de f(x) lorsque x tend vers a est infinie, nous appelons la droite x=a une asymptote verticale.
En résumé, nous avons étudié les limites de fonctions lorsque x tend vers a. Dans certains cas, les fonctions tendent vers l'infini ou converge vers une valeur finie. Nous avons également introduit la notion d'asymptote verticale pour les limites plus l'infini en un point fini. N'hésitez pas à poser des questions supplémentaires ou à discuter avec d'autres dans la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc
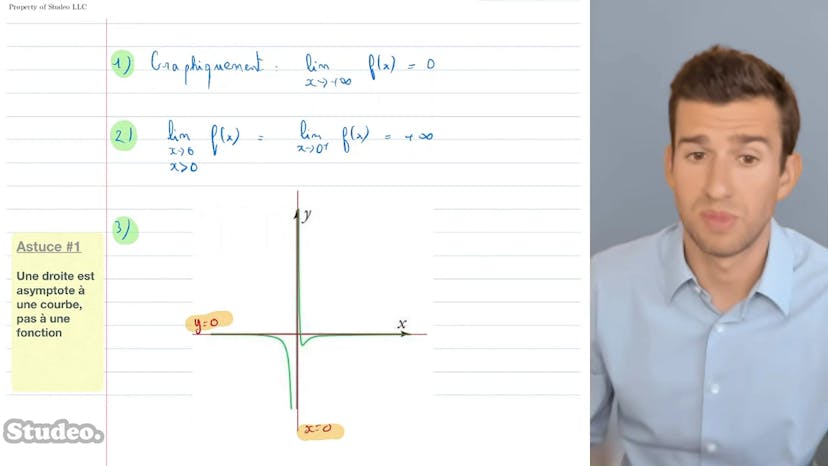
Analyse graphique
Bonjour à tous ! Aujourd'hui, nous allons aborder la notion de limite des fonctions à travers une analyse graphique. Nous observons la courbe de la fonction tracée et tentons de déterminer ses limites.
Lorsque x tend vers plus l'infini, nous constatons que la fonction tend vers 0. Ce sera donc notre première limite. Ensuite, lorsque x tend vers 0 par une valeur positive, nous remarquons que la courbe s'élève vers plus l'infini. Nous en déduisons que la fonction admet deux asymptotes : une verticale en x=0 et une horizontale pour les valeurs plus et moins l'infini.
Lorsque nous cherchons les équations des asymptotes, nous notons que les équations des droites horizontales sont toujours de la forme y=a, tandis que les droites verticales sont de la forme x=a. Dans notre cas, l'équation de l'asymptote horizontale est y=0 et l'asymptote verticale est x=0.
Il est important de préciser que l'on dit qu'une droite est asymptote à une courbe, et non à sa fonction. De plus, il est tout à fait possible qu'une droite soit asymptote en deux endroits, comme c'est le cas ici avec l'asymptote horizontale en plus et moins l'infini.
Ceci conclut notre introduction sur la limite des fonctions. Si vous avez des questions, n'hésitez pas à les poser.
Maths SM&SP
Analyse
2BAC SM Maroc

Calcul limite en un point fini par factorisation
Lors de ce cours, nous apprenons une méthode pour trouver la limite d'une fonction lorsque nous avons une forme indéterminée. Pour cela, nous pouvons souvent factoriser pour lever cette indétermination.
Dans le premier exemple, nous avons la fonction f(x) = (x²-2x)/(x-1). En utilisant l'identité remarquable (x-1)² = x²-2x+1, nous pouvons simplifier cette fonction en f(x) = (x-1). Ainsi, la limite de f(x) lorsque x tend vers 1 est 0, que ce soit de la droite ou de la gauche.
Dans le deuxième exemple, nous avons la fonction g(x) = (x²-2x+1)/(2x-2). En factorisant par 2, nous obtenons g(x) = (x-1)²/(2(x-1)). Pour trouver les racines de ce polynôme, nous calculons le discriminant qui est égal à 1. Les racines x₁ et x₂ sont donc 1 et 2. En utilisant la méthode des racines évidentes, nous pouvons directement trouver x=1 comme racine. Ainsi, nous factorisons g(x) en g(x) = 2(x-1)(x-2)/(2(x-1)). Simplifiant cette expression, nous obtenons g(x) = (x-1)/(x-1) = 1. La limite de g(x) lorsque x tend vers 1 est donc 1.
En conclusion, la méthode enseignée dans ce cours consiste à factoriser la fonction pour lever l'indétermination et trouver la limite. Cette méthode peut être très utile et il est important de s'entraîner sur ce type d'exercices pour la maîtriser.
Maths SM&SP
Analyse
2BAC SM Maroc

Determiner une asymptote + étude
Dans ce cours, nous apprenons à trouver les asymptotes d'une fonction. Les asymptotes peuvent être situées à moins l'infini, à plus l'infini, aux deux, ou sur les bords de l'ensemble de définition de la fonction. Pour trouver ces asymptotes, nous devons prendre en compte les valeurs interdites de la fonction. Dans l'exemple donné, la fonction f(x) est égale à -2/(1-x) et est définie sur R privé de 1. Nous regardons d'abord les asymptotes à moins l'infini et à plus l'infini. En utilisant le quotient, nous constatons que f(x) tend vers moins l'infini à x=0. Par conséquent, nous avons une asymptote horizontale y=0 pour les valeurs extrêmes. En analysant la fonction en x=1, nous constatons que 1-x tend vers 0 en approchant x de 1 par la gauche et par la droite. En utilisant le quotient, nous déterminons que f(x) tend vers moins l'infini en s'approchant de 1 par la gauche et vers plus l'infini en s'approchant de 1 par la droite. Ainsi, nous avons une asymptote verticale x=1 pour cette valeur interdite. En résumé, pour trouver les asymptotes, nous examinons les tendances à plus l'infini, à moins l'infini et sur les bords de l'ensemble de définition de la fonction.
Maths SM&SP
Analyse
2BAC SM Maroc

Calcul de limite infinie avec la définition (trouver un A)
Dans ce cours, nous abordons la définition formelle de la limite. Il s'agit d'un concept important en mathématiques, qui peut être difficile à comprendre au début.
La limite d'une fonction consiste à dire que lorsque la variable x tend vers l'infini, la valeur de la fonction tend également vers l'infini. En d'autres termes, peu importe la valeur à laquelle je fixe ma hauteur, il y aura toujours un moment où la fonction la dépassera et restera toujours au-dessus.
Pour illustrer cela, nous avons tracé une fonction de type racine carrée de x. Peu importe la valeur choisie pour m, il y aura toujours une valeur a à partir de laquelle la fonction sera au-dessus de cette hauteur.
Ensuite, nous appliquons cette définition à un exemple spécifique où f(x) est égal à la racine carrée de x^2 -1. Nous devons montrer l'existence d'un a pour chaque valeur de m. Pour cela, nous résolvons l'inéquation f(x) > m. En passant au carré, nous obtenons x^2 > m + 1.
En gardant à l'esprit que nous nous intéressons à la limite vers l'infini, nous prenons la solution positive et obtenons x > racine carrée de m^2 + 1. Cela nous permet de trouver la valeur a appropriée. En utilisant cette valeur dans l'autre sens, nous pouvons montrer que f(x) > m lorsque x > a. Cela confirme que la fonction tend bien vers l'infini lorsque x tend vers l'infini.
Il est important de s'exercer avec différentes fonctions pour maîtriser cette méthode de résolution d'équations et de retrouver la valeur a correspondante. Au final, il s'agit simplement d'appliquer la définition formelle de la limite.
Maths SM&SP
Analyse
2BAC SM Maroc
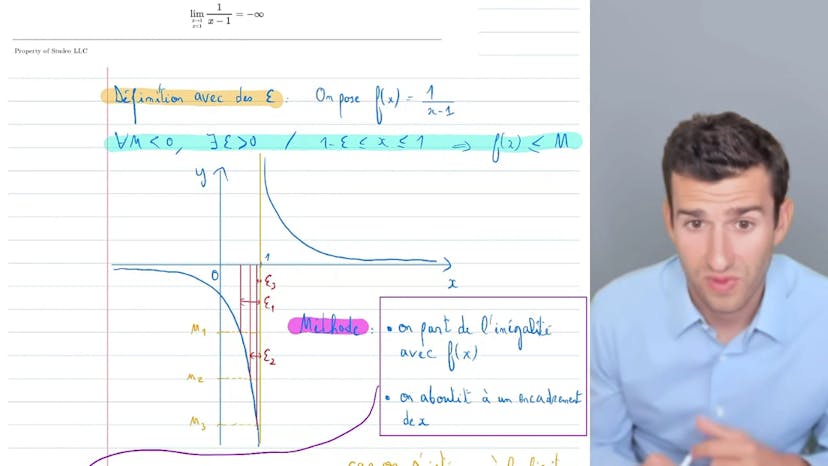
Calcul de limite finie avec la définition (trouver un epsilon)
Dans ce cours, nous étudions le calcul de la limite finie. Nous avons déjà examiné la notion de limite infinie et nous nous concentrons maintenant sur une limite spécifique fixée, utilisant la définition avec les épsilon.
Pour comprendre comment utiliser les épsilon, nous les utilisons pour montrer que la fonction tend vers moins l'infini, de manière similaire. Peu importe la limite fixée, aussi petite soit-elle, il y aura nécessairement un moment où la fonction sera inférieure dans une plage de valeurs négatives. En fait, lorsque je serai à une distance de épsilon proche de 1, je serai en dessous de cette limite. Donc, l'idée est que j'aurai un intervalle du type 1-épsilon1 où la fonction sera inférieure à M. J'ai donné quelques exemples avec la fonction 1/(x-1) pour illustrer cela.
La méthode est la même, nous partons de l'inégalité f(x) ≤ M et nous essayons de résoudre f(x) - M pour trouver l'encadrement de x qui nous permettra de déterminer le épsilon approprié.
Nous commençons avec un réel M négatif et regardons la limite en 1- pour x-1. Nous résolvons f(x) - M, ce qui donne 1/(x-1) - M. Nous examinons ensuite 1/(x-1) - M ≤ 0, et sachant que la fonction inverse est décroissante sur ℝ*, nous devons vérifier si nous sommes sur ℝ- ou ℝ+. Nous souhaitons encadrer x, nous devons donc avoir x > 1-1/M, en tenant compte du fait que 1/M est négatif. Ainsi, nous avons l'encadrement voulu : x < 1 et x > 1-1/M.
Maintenant, nous avons notre épsilon, qui est égal à 1-1/M. Si nous prenons épsilon de cette valeur, dans tout l'intervalle 1-épsilon à 1, notre fonction f(x) sera inférieure à M, ce qui correspond exactement à ce que nous voulions démontrer.
Ainsi, nous avons démontré rigoureusement, en utilisant les calculs de limites, les définitions et les épsilon, que la limite lorsque x tend vers 1- (par valeurs négatives de 1/(x-1)) est égale à moins l'infini.
Il est important de s'exercer avec des exercices équivalents pour mieux comprendre la méthode.
En résumé, pour utiliser cette méthode, nous partons de l'inégalité f(x) ≤ M et nous trouvons l'épsilon approprié en utilisant 1-1/x, en déroulant progressivement.
C'est tout pour cette méthode.
Maths SM&SP
Analyse
2BAC SM Maroc
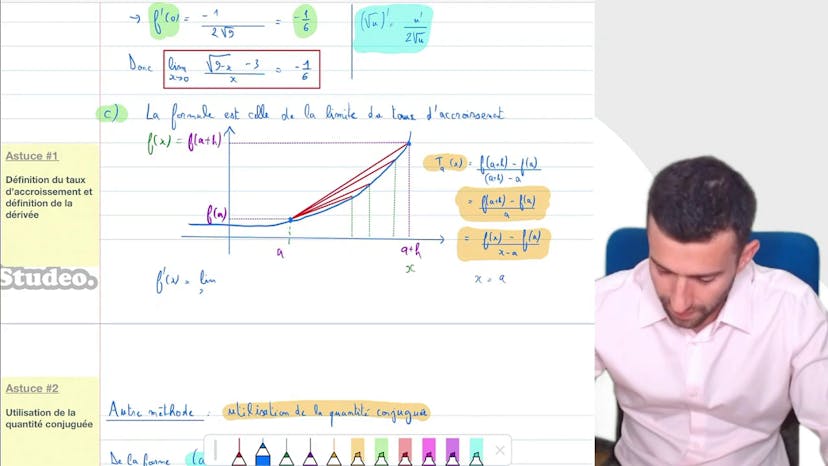
Utilisation de la dérivée
Dans ce cours, nous étudions les limites en utilisant le taux d'accroissement et la dérivée. L'exercice consiste à trouver plusieurs limites en utilisant cette méthode.
L'enseignant souligne que repérer les limites n'est pas toujours facile et nécessite de l'entraînement. Il suggère aux étudiants de poser des questions dans la section des commentaires si certains points ne sont pas clairs.
Dans le premier exemple, l'enseignant explique comment utiliser la dérivée pour trouver la limite d'une fonction donnée. Il rappelle la définition du taux d'accroissement et explique comment calculer la dérivée.
Le deuxième exemple traite d'une autre limite en utilisant la même méthode. L'enseignant montre comment choisir la fonction appropriée et calculer la dérivée.
Dans le troisième exemple, l'enseignant montre qu'il y a une erreur dans le problème initial. Il explique comment vérifier si la limite est indéterminée et comment rectifier l'erreur.
En conclusion, l'enseignant encourage les étudiants à s'entraîner davantage sur les exercices similaires et à poser des questions s'ils ont des difficultés.


