Cours d'apprentissage en ligne

Continuité et suites : Théorème du point fixe

Une application importante de l'étude de la continuité est l'étude des suites. Le théorème du point fixe est un résultat fondamental qui s'applique à une fonction continue f sur un intervalle I et à une suite un définie de manière récurrente. Si la suite un converge vers l, qui appartient à I, alors f(l) = l. Ce théorème repose sur la continuité de la fonction f. La démonstration utilise la définition de la continuité et montre que f(un) converge également vers f(l), ce qui implique que l = f(l). Il est important de noter que ce résultat ne s'applique que si la fonction est continue. Ensuite, le cours rappelle que les convergences de suites définies de manière récurrente peuvent avoir des comportements différents en fonction de la forme de la fonction f. On peut observer une convergence en escalier ou une convergence en escargot, en fonction des variations de la fonction et de la suite.

TVI : LE théorème

Le théorème des valeurs intermédiaires est un concept fondamental en mathématiques, notamment pour l'étude des fonctions et la résolution d'équations. Ce théorème stipule que si f' est une fonction continue sur un intervalle [a, b] et si k est un nombre réel compris entre f(a) et f(b), alors l'équation f(x) = k admet au moins une solution c dans l'intervalle [a, b]. Pour illustrer ce théorème, considérons une courbe représentant une fonction cubique. L'intervalle [a, b] est défini comme la portion de la courbe entre deux points spécifiques. En traçant la fonction, nous voyons que celle-ci fluctue entre ces deux points de manière continue, sans lever le stylo. En conséquence, si nous traçons une droite horizontale pour une valeur k entre f(a) et f(b), il est inévitable que la courbe de la fonction croise cette droite quelque part entre les points a et b. Ainsi, l'équation f(x) = k a toujours au moins une solution. Dans certaines situations, où la fonction est strictement croissante ou décroissante, il n'y aura qu'un seul point d'intersection entre la courbe et une droite horizontale. Cela est dû à l'absence de fluctuations dans la direction de la courbe. Il est important de souligner que l'utilisation de ce théorème repose sur la continuité de la fonction. Ainsi, il convient de mentionner explicitement le théorème des valeurs intermédiaires lors de sa justification. En conclusion, le théorème des valeurs intermédiaires, également appelé théorème de la bijection dans les cas de stricte croissance ou décroissance, permet de garantir l'existence d'au moins une solution à une équation donnée sur un intervalle spécifié.

Continuité en un Point

Dans ce cours, nous étudions comment trouver la dérivée d'une fonction avec plusieurs expressions sur différents intervalles. Nous constatons que la fonction peut être continue mais pas dérivable. Par exemple, pour la fonction f qui est définie par trois expressions sur trois intervalles, nous vérifions si elle est parfaitement continue. Pour qu'une fonction soit continue, il faut d'abord qu'elle soit définie. Dans notre exemple, la fonction est bien définie sur les intervalles donnés. En dehors des limites entre les intervalles, la fonction est continue de façon satisfaisante. Nous nous concentrons alors sur la continuité aux points 3 et 5, qui correspondent aux extrémités des intervalles. Comme il y a deux expressions différentes à gauche et à droite de 3, nous examinons la limite lorsque x tend vers 3 avec x inférieur à 3, et lorsque x tend vers 3 avec x supérieur à 3. Il est essentiel que ces limites soient égales et égales à f(3) pour que la continuité soit satisfaite. Dans notre cas, les limites et f(3) remplissent ces conditions, donc la fonction est continue en 3. Nous répétons ensuite le même processus pour le point 5. Cependant, nous constatons que les expressions ne sont pas les mêmes pour les limites à gauche et à droite de 5. Par conséquent, la fonction n'est pas continue en 5. Dans les prochaines étapes, nous examinerons également la dérivabilité de la fonction.

Dérivabilité en un Point

La fonction étudiée est f(x) = |x|^2 + 2x - 3. On constate graphiquement que cette fonction n'est pas dérivable en x = -3 et x = 1, car il y a une discontinuité de la pente à ces points. Cependant, la fonction est dérivable sur l'ensemble des autres points de R, à l'exception de -3 et 1. Ceci est dû au fait que la valeur absolue n'est pas dérivable en 0, mais reste continue. Donc, par composition avec un polynôme continu, la fonction globale reste continue et dérivable à l'exception de -3 et 1.

Prolongement par Continuité

Dans ce cours, nous abordons le concept de prolongement par continuité en mathématiques. Dans certains cas, une fonction peut ne pas être définie en un certain point, mais si la limite de cette fonction existe et est finie, il est possible de prolonger cette fonction par continuité en ce point. Pour ce faire, on pose la valeur de la fonction en ce point égal à la limite de la fonction quand x se rapproche de ce point. Ainsi, on crée une fonction qui est définie et continue en ce point. Par exemple, si nous considérons la fonction f(x) = x/x, cette fonction n'est pas définie en 0 à cause du dénominateur, mais on peut prolonger cette fonction par continuité en posant f(0) = 1. Ainsi, la fonction est définie et continue en 0. Dans un autre exemple, on nous propose une fonction f(x) = {x sin(1/x) si x ≠ 0, 0 si x = 0}. Cette fonction n'est pas définie en 0 à cause du terme 1/x, mais on peut conjecturer que cette fonction est continue en 0 en observant son graphique. Pour prouver cela, nous utilisons le théorème d'encadrement en utilisant la valeur absolue pour encadrer le sinus. Nous montrons alors que la fonction tend vers 0 en utilisant le théorème d'encadrement, ce qui prouve que la fonction est bien continuée en 0. En utilisant cette méthode de prolongement par continuité, nous pouvons donc étendre la définition d'une fonction et l'assurer continues en des points où elle n'était pas initialement définie.

TVI et Fonction Auxiliaire

Le cours aborde le théorème des valeurs intermédiaires en utilisant l'étude d'une fonction spécifique. La fonction f(x) est définie comme étant égale à 10x sur e^x plus 1. L'ensemble de définition de la fonction est [0, +∞) car le dénominateur, e^x plus 1, est strictement positif pour toutes les valeurs de x dans cet intervalle. La première étape consiste à vérifier que la fonction est bien définie et dérivable sur son ensemble de définition. Comme e^x plus 1 ne s'annule jamais à cause de l'exponentiel et du plus 1, il n'y a aucun problème et la fonction est donc bien définie et dérivable. En calculant la dérivée de la fonction f(x), on obtient f'(x) = (1 - x)e^x. On utilise ensuite cette dérivée pour déterminer les variations de la fonction f. En étudiant le signe de chaque facteur de la dérivée, on trouve que f'(x) est strictement négatif pour tout x dans l'intervalle [0, +∞), ce qui implique que la fonction f est strictement décroissante sur cet intervalle. Selon le théorème des valeurs intermédiaires, on démontre qu'il existe un unique réel alpha tel que f(alpha) = 0. Cette démonstration s'appuie sur la continuité de la fonction f sur son ensemble de définition, ainsi que sur le fait que la fonction est strictement décroissante. Pour trouver une estimation de la valeur de alpha, on peut utiliser une calculatrice pour encadrer la valeur de alpha entre deux réels donnés. Dans cet exemple, on trouve que alpha est compris entre 1,28 et 1,29. En étudiant le signe de la fonction f selon les valeurs de x, on constate que f est positive sur l'intervalle [0, alpha] et négative sur l'intervalle [alpha, +∞). Cette information permet de dresser le tableau de variations de la fonction f. Les limites de la fonction f sont également étudiées. On trouve que f(0) = 0 et que la limite de f(x) lorsque x tend vers l'infini est 0. Cela signifie que la fonction f a une asymptote horizontale y = 0. En conclusion, le cours explique comment appliquer le théorème des valeurs intermédiaires en utilisant une fonction auxiliaire pour étudier une fonction plus complexe. Il souligne également l'importance de la stricte monotonie dans l'unicité des solutions.

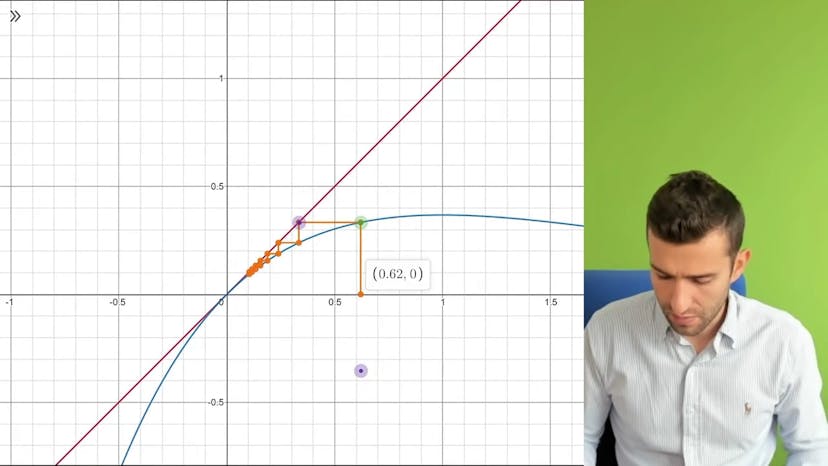
Continuité et suites 1

Ce cours porte sur le calcul d'une limite d'une suite définie par récurrence. La méthode consiste à trouver les points fixes de la fonction de récurrence et à vérifier si la suite converge vers l'un de ces points. Si la fonction est continue, alors la limite de la suite est un point fixe. Si la fonction n'est pas continue, cette méthode ne fonctionne pas. Il est important de justifier la continuité de la fonction pour appliquer cette méthode. Le premier terme de la suite peut également avoir une influence sur sa convergence, il est donc essentiel de le prendre en compte. Si la suite ne converge pas vers un point fixe, alors elle n'a pas de limite. Dans l'exemple donné, la fonction de récurrence est f(x) = x * (e^2 - x), et le point fixe est x = 0. La limite de la suite est donc 0 si le premier terme est positif. Dans un autre exemple où la fonction n'est pas continue, la suite ne converge pas vers le point fixe. Il est donc nécessaire de prendre en compte la continuité de la fonction pour utiliser cette méthode.

Continuité et Suites 2

Dans ce cours, nous étudions les suites définies par récurrence et comment trouver leur limite. Tout d'abord, nous associons une fonction f à la suite et définissons la suite de manière à ce que u(n+1) = f(u(n)). Nous commençons par étudier la fonction f et sa continuité est essentielle. Ensuite, nous résolvons l'équation f(x) = x pour trouver les solutions possibles pour la limite de la suite. Ensuite, nous étudions la dérivabilité de la fonction f et utilisons la méthode de dérivation pour déterminer si elle est croissante. Il est important de noter que la fonction f peut ne pas être définie pour certains points, ce qui affecte sa croissance. Ensuite, nous démontrons par récurrence que la suite est strictement croissante et bornée. Cela nous permet de conclure que la suite converge vers une limite. En utilisant la continuité de f et les propriétés de la suite, nous pouvons déterminer la limite en trouvant la valeur qui satisfait f(x) = x. La continuité de f est cruciale car elle garantit que la limite recherchée est bien une solution. Une autre fonction f qui n'est pas continue envoie la suite vers une limite différente, ce qui souligne l'importance de la continuité pour appliquer le théorème. En conclusion, ce cours explique la méthode pour trouver la limite des suites définies par récurrence en utilisant la continuité de la fonction f et la propriété de récurrence.

Saut de continuité

Le cours aborde la notion de continuité d'une fonction et propose des exercices pratiques pour illustrer cette notion. Le premier exercice consiste à déterminer si une fonction donnée est continue en utilisant la méthode de la quantité conjuguée. La deuxième méthode utilisée est celle de la dérivabilité pour déterminer si la fonction est continue. La question suivante demande quelle valeur de m permet à la fonction d'être continue en 0, en utilisant la définition fondamentale de la continuité. La réponse est que m doit être égal à 0.

TVI et expo

Dans ce cours, nous étudions graphiquement le nombre de solutions de l'équation E-x² = E2x-1. Nous observons les courbes des deux fonctions E-x² et E2x-1. La courbe de E-x² est une courbe en cloche de probabilité. Nous remarquons que la fonction noire est au-dessus de la fonction rouge pour les nombres négatifs, mais qu'il y a un changement de comportement aux nombres positifs où les deux fonctions s'intersectent. Nous séparons ensuite l'étude en deux parties : R- (les nombres négatifs) et R+ (les nombres positifs). Sur R-, nous démontrons que la fonction en cloche E-x² est strictement supérieure à l'autre fonction, ce qui prouve qu'il n'y a pas de solutions à l'équation dans cette plage de nombres. Sur R+, nous posons f2x = E-x² - E2x-1 et étudions sa décroissance. En utilisant les propriétés de l'exponentielle, nous montrons que f2x est strictement décroissante sur 0 plus l'infini. En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe une unique solution à l'équation sur R+. Finalement, nous concluons qu'il n'y a pas de solutions sur R- et une unique solution sur R, ce qui confirme notre intuition graphique. En résumé, l'équation E-x² = E2x-1 a une unique solution sur l'ensemble des réels.

TVI et calculs costauds !

La fonction f(x) = 2/(e^x + e^(-x)) représente une somme d'exponentielles positives strictes, ce qui exclut la possibilité d'obtenir une valeur égale à zéro. En regardant graphiquement le nombre de solutions de l'équation f(x) = x, il est clair qu'il n'y a qu'une seule solution unique. Pour montrer que la fonction g(x) = f(x) - x est décroissante, nous commençons par dériver la fonction f(x) et simplifier. La dérivée de f(x) est -2(e^x - e^(-x))/(e^x + e^(-x))^2. Après des calculs plus avancés, nous obtenons que la dérivée de g(x) est égale à -2(e^(2x) + 1)(e^(-2x) - 1)/(e^(2x) + e^(-2x))^2, ce qui est toujours négatif. Par conséquent, nous pouvons conclure que g(x) est décroissante. En utilisant le Théorème des Valeurs Intermédiaires, nous pouvons affirmer qu'il existe un unique nombre alpha tel que f(alpha) = alpha. Ainsi, l'équation f(x) = x admet une seule solution.