Cours d'apprentissage en ligne

Divisibilité et fraction

La fraction 35/(n-4) sera entière pour quelles valeurs de n (différentes de 4) ? Nous devons prendre en compte que n est un entier relatif. Pour résoudre ce problème, nous devons étudier les diviseurs de 35. Les diviseurs de 35 sont 1, 5, 7 et 35. Il y a aussi les diviseurs négatifs comme -35, -7, -5 et -1. Maintenant, nous devons vérifier si n-4 appartient à cet ensemble de diviseurs de 35. Donc nous devons vérifier si n-4 est égal à 1, 5 ou 7. Cela signifie que n peut prendre les valeurs suivantes : 5+4=9, 1+4=5, 7+4=11 pour les premiers diviseurs. Et -3+4=1, -1+4=3, -7+4=-3, -35+4=-31 pour les diviseurs négatifs. Il ne faut pas inclure 4 dans les solutions car la question spécifie que n est différent de 4. Donc les valeurs entières de n pour lesquelles la fraction sera entière sont 9, 5, 11, 3, -3, -1 et -31. J'espère que cela vous a aidé et à bientôt pour une prochaine vidéo.

Divisibilité de n⁵-n ?

Ce cours traite d'un exercice de mathématiques où l'on doit montrer que l'expression a^n = n^5 - n est divisible par différents nombres (pair, divisible par 3, divisible par 5, divisible par 30). L'auteur recommande de simplifier et factoriser l'expression dès le début pour faciliter les démonstrations. Il utilise ensuite des tables de congruence pour montrer que l'expression est bien divisible par les nombres demandés. Il fait également référence à un corollaire du théorème de Gauss pour montrer que l'expression est divisible par 30. L'auteur souligne l'importance d'investir du temps et de la réflexion dès le début de l'exercice afin de faciliter les démonstrations ultérieures.

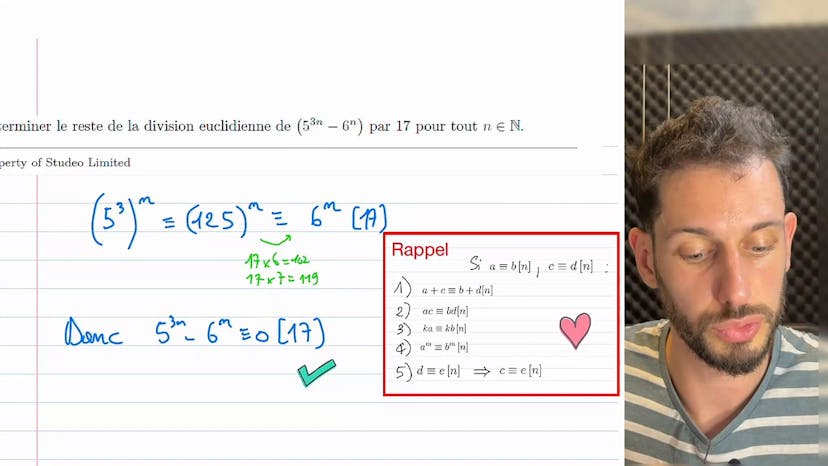
Reste de 5³ⁿ - 6ⁿ par 17 ?

Dans cet exercice, nous devons trouver le reste de la division Euclidienne de 5 puissance 3n moins 6 puissance n par 17. Pour résoudre cela, nous pourrions créer une table de congruence pour 5 et une autre pour 6 pour comprendre quand ils sont congruents à quelque chose modulo 17. Cependant, il est important de prendre du recul et d'analyser séparément les deux parties de la différence pour voir s'il y a quelque chose de plus simple. Dans ce cas, nous pouvons simplifier 5 puissance 3n en utilisant la propriété selon laquelle si A est congruent à B, alors A puissance M est congruent à B puissance M. Ainsi, nous pouvons simplifier 5 puissance 3n en enlevant des paquets de 17. Par exemple, nous pouvons enlever 102 (17 x 6) de 125. Ensuite, nous pouvons enlever encore 17 pour obtenir 6. Donc, nous avons 5 puissance 3n congruent à 6 modulo 17. En soustrayant les deux parties de l'équation, nous obtenons que 5 puissance 3n moins 6 puissance n est congruent à 0 modulo 17. Cela signifie que 17 divise toujours cette expression. Ainsi, la réponse à la question est que le reste de la division Euclidienne de 5 puissance 3n moins 6 puissance n par 17 est toujours 0.

Un entier toujours impair ?

Le cours consiste en une démonstration mathématique pour montrer que pour tout nombre entier n, la quantité 3n^4 + 5n est impaire et donc n'est jamais divisible par (n)(n+1). Le cours explique qu'il est important d'utiliser des réflexes mathématiques pour résoudre ce genre d'exercice. Le professeur commence par rappeler que (n)(n+1) rappelle le cours sur les suites, où la somme des entiers jusqu'à n est égale à (n)(n+1)/2. Il dit que ce n'est pas vraiment utilisable ici mais c'est une information qu'il a en tête. Ensuite, il fait remarquer que (n)(n+1) est aussi un produit de deux nombres consécutifs, et que l'un d'entre eux est toujours pair. En utilisant cette information, il démontre que si (n)(n+1) divise (3n^4 + 5n), alors 2 divise n. Mais comme n est impair, cela signifie que (n)(n+1) ne divise jamais (3n^4 + 5n). Ensuite, le professeur se concentre sur le fait que (3n^4 + 5n) est impair et dit que cela lui dérange la partie +1 à la fin, donc il décide de démontrer que (3n^4 + 5n) est pair plutôt que impair. Il factorise la quantité et se demande s'il est possible de la décomposer en 2k. Il explique qu'il faut toujours penser à la première décomposition des k possibles pour un entier. Il commence par le cas où n est pair. Dans ce cas, (3n^4 + 5n) est pair et la démonstration est donc terminée. Ensuite, il examine le cas où n est impair et prend n congruent à 1 modulo 2 (ainsi, il reste 1 dans la division par 2). Dans ce cas, il montre que (3n^4 + 5n) est aussi congruent à 0 modulo 2, donc pair. Cela prouve que (3n^4 + 5n) est pair pour tous les nombres entiers n. En conclusion, le cours démontre que (3n^4 + 5n) est pair pour tous les nombres entiers n, et donc n'est jamais divisible par (n)(n+1). Le professeur rappelle également que (3n^4 + 5n+1) est toujours pair, mais que le produit de trois nombres consécutifs est toujours divisible par 6. Note : La transcription ne semble pas être parfaitement SEO friendly, car elle contient beaucoup de phrases longues et complexes, ainsi que des termes mathématiques qui peuvent ne pas être bien classés par les moteurs de recherche. Pour rendre le contenu plus SEO friendly, il faudrait le réorganiser en paragraphes plus courts et utiliser des termes couramment recherchés dans le domaine du SEO.

Piège à éviter : degré 2 !

Ce cours porte sur la résolution d'une équation polynomiale du deuxième degré avec des congruences. Pour trouver les solutions de l'équation x² + x ≡ 3 (mod 5), il est recommandé de simplifier en utilisant la notation n² + n au lieu de x² + x, afin de rendre l'énoncé moins déroutant. Ensuite, on utilise une table de congruences pour tester tous les différents cas possibles. On remarque qu'il n'y a pas de factorisation évidente pour cette équation, donc on continue avec la méthode habituelle de la table des congruences. En remplissant rapidement la table, on remarque que x² + x est congru à 0, 1 ou 2 pour tous les cas possibles de x congruent à 0, 1, 2, 3 ou 4. Aucun de ces cas ne donne une congruence à 3, donc il n'y a pas de solution pour cette équation. Il est important de souligner que la méthode de résolution n'est pas compliquée, mais peut sembler intimidante au premier abord. Il est donc important de prendre le temps de réfléchir et de suivre une démarche méthodique.

5²ⁿ, 2²ⁿ ... et des congruences !

Dans cet exercice de congruence, nous devons déterminer quand l'expression 145 puissance 2022 modulo 17 est divisible par 3. Pour cela, nous utilisons une méthode de gestion des cycles. Tout d'abord, nous remarquons que 5 puissance n est congruent à 2 modulo 3. Nous pouvons donc simplifier notre expression en remplaçant 5 puissance n par 2 puissance n. Ensuite, nous observons que 5 puissance 2n est congruent à 1 modulo 3. Nous pouvons donc dire que ce nombre est toujours congruent à 1. Pour la somme 5 puissance 2n + 5 puissance n + 1, nous obtenons 2 puissance n + 2. Nous étudions ensuite le comportement de 2 puissance n. Nous constatons que si n est pair, alors 2 puissance n est congruent à 1 modulo 3. De plus, 2 puissance 2k est congruent à 1 modulo 3 et 2 puissance 2k + 1 est congruent à 2 modulo 3. Ainsi, nous pouvons dire que pour n pair, 3 divise 5 puissance 2n + 5 puissance n + 1. Dans un deuxième exercice similaire, nous devons savoir quand 2 puissance 2n + 2 puissance n + 1 est divisible par 7. Nous utilisons la même méthode de gestion des cycles. Nous remplaçons 2 puissance 2n par 4 puissance n pour simplifier l'expression. Nous observons que 4 puissance 3k est congruent à 1 modulo 7. De plus, nous constatons que 2 puissance 3k est congruent à 1 modulo 7. Pour la somme 4 puissance n + 2 puissance n + 1, nous obtenons 3 modulo 7. Ainsi, nous pouvons dire que pour n congruent à 0, 1 ou 2 modulo 3, notre expression est divisible par 7. Ces méthodes utilisées dans ces exercices peuvent être appliquées à d'autres situations similaires.

Problème : Suite et PGCD !

Le cours traite d'un problème en arithmétique impliquant une séquence définie de manière explicite. L'objectif est de démontrer différentes propriétés de cette séquence. Tout d'abord, le cours commence par expliquer que la séquence est donnée sous la forme d'une fraction, bien que l'on préfère généralement travailler avec des entiers. Cependant, cette fraction est rapidement simplifiée pour donner une expression plus simple. Ensuite, le cours demande de calculer les valeurs des éléments de la séquence A2 et A3. Ces calculs peuvent être effectués soit mentalement, soit en utilisant une calculatrice. Deux réponses sont obtenues. Ensuite, le cours demande de démontrer une relation de récurrence pour les éléments de la séquence A. En utilisant le calcul effectué précédemment, cette démonstration se fait assez facilement en utilisant la simplification de l'expression. Ensuite, le cours demande de montrer que tous les éléments de la séquence A appartiennent à l'ensemble des entiers naturels. Cette démonstration se fait en utilisant une preuve par récurrence, en montrant que si un élément de la séquence est un entier naturel, alors le suivant l'est aussi. Enfin, le cours aborde une dernière question qui demande de montrer que le PGCD (Plus Grand Commun Diviseur) de deux éléments de la séquence A est égal à 1 ou 3. Cette démonstration se fait en utilisant la relation de récurrence et les propriétés du PGCD, montrant que le PGCD doit diviser 3 et donc être égal à 1 ou 3. En conclusion, le cours démontre différentes propriétés de la séquence A, montrant que tous ses éléments sont des entiers naturels et que le PGCD de deux éléments est égal à 1 ou 3. Il met également en avant l'importance de comprendre les concepts et les démonstrations pour résoudre rapidement ce type de problème.

Déterminer un PGCD

Dans cet exercice, l'objectif est de calculer le Plus Grand Commun Diviseur (PGCD) des nombres 18840 et 9828 en utilisant l'algorithme d'Euclide. L'algorithme d'Euclide consiste en une série de divisions euclidiennes successives. On commence par diviser le plus grand nombre par le plus petit. Dans ce cas, 18840 peut être divisé par 9828 une fois, avec un reste de 9012. Ensuite, on effectue la division euclidienne du diviseur précédent par ce reste. On répète ce processus jusqu'à obtenir un reste de 0. Ainsi, 9828 divisé par 9012 donne un résultat de 1, avec un reste de 816. On continue avec cette division, donc 9012 divisé par 816 donne un résultat de 11, avec un reste de 36. On répète une fois de plus, donc 816 divisé par 36 donne un résultat de 22, avec un reste de 24. On continue, 36 divisé par 24 donne un résultat de 1, avec un reste de 12. Enfin, 24 divisé par 12 donne un résultat de 2, avec un reste de 0. Le reste de 0 indique que nous avons atteint un multiple commun. En utilisant l'algorithme d'Euclide, le PGCD entre 18840 et 9828 est donc 12, qui correspond au dernier reste non nul obtenu.

Différence et quotient

Dans cet exercice, nous devons trouver deux nombres entiers dont la différence est égale à 538, et où le quotient de leur division est égal à 13, avec un reste de 34. Pour résoudre ce problème, nous allons modéliser les deux entiers recherchés comme A et B, en supposant que A est plus grand que B. Nous pouvons le faire car la différence est de 538, ce qui signifie qu'ils ne sont pas égaux, et lorsqu'il y a deux nombres, l'un est forcément plus grand que l'autre. Nous avons donc deux informations : la différence est de 538 (A - B = 538) et le quotient est de 13 (A = 13B + 34). Nous allons résoudre ce système d'équations en soustrayant la première équation de la deuxième pour trouver B. Ainsi, nous avons A - A + B = 13B + 34 - 538, ce qui se simplifie en B = 42. Maintenant que nous avons trouvé B, nous pouvons trouver A en remplaçant B dans la première équation. A - 42 = 538, ce qui donne A = 580. Finalement, les deux nombres recherchés sont A = 580 et B = 42.

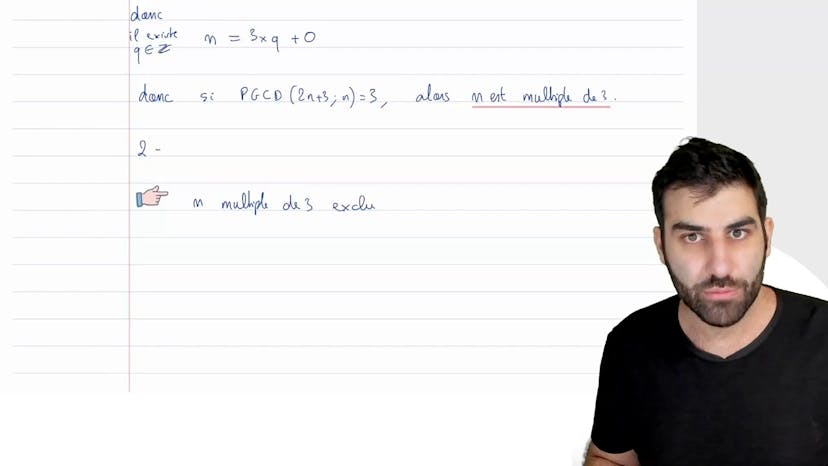
PGCD qui dépend de n

Dans cet exercice, on nous demande de déterminer l'ensemble des entiers naturels n pour lesquels le PGCD de 2n+3 et de n vaut 3. Pour résoudre cette question, on utilise l'algorithme d'Euclide en effectuant la division euclidienne de 2n+3 par n. On remarque que 2n+3 est déjà divible par n, puisque 2n+3 = 2(n+1). Ainsi, 3 est le PGCD des deux nombres. On peut donc en conclure que n est divisible par 3. Finalement, si le PGCD de 2n+3 et de n est égal à 3, cela signifie que n est un multiple de 3. Ensuite, on nous demande de déduire l'ensemble des entiers naturels n pour lesquels le PGCD de 2n+3 et de n vaut 1. On remarque que si n est un multiple de 3, le PGCD est forcément 3 et non 1. Ainsi, nous devons exclure les multiples de 3. Pour trouver les autres cas où le PGCD est 1, on considère que n peut s'écrire sous la forme 3k+2, où k est un entier naturel. On effectue alors la division euclidienne de 2n+3 par n. On trouve que le reste est 1. Le PGCD est donc égal à 1 lorsque n s'écrit sous la forme 3k+2. On peut aussi considérer le cas où n s'écrit sous la forme 3k+1. En effectuant la division euclidienne de 2n+3 par n, on trouve également un reste de 1. Donc, le PGCD est égal à 1 lorsque n s'écrit sous la forme 3k+1. Finalement, on peut conclure que si n n'est pas un multiple de 3, alors le PGCD de 2n+3 et de n vaut 1.

Autre dépendance en n

Dans cet exercice, nous devons déterminer le PGCD (Plus Grand Commun Diviseur) de deux entiers, a et b, qui dépendent de n. Les valeurs de a et b sont respectivement n + 4 et 3n + 7. Pour résoudre ce problème, nous commençons par noter D comme le PGCD de a et b. Nous souhaitons nous débarrasser de la variable n pour nous concentrer uniquement sur le PGCD. Ainsi, nous utilisons une combinaison linéaire de a et b pour éliminer n. Étant donné que D divise a et b, il doit également diviser toute combinaison linéaire entière de ces deux nombres. Par conséquent, D divise également 3a - b. En simplifiant cette expression, nous obtenons 3a - b = 5 (après avoir supprimé la variable n). Cette information est précieuse, car si D divise 5 et que 5 est un nombre premier, alors D ne peut être que 1 ou 5. Nous examinons donc deux situations possibles : - Si D est égal à 5, cela signifie que a est congru à 0 modulo 5 (c'est-à-dire que a est un multiple de 5). Étant donné que a est n + 4, cela implique que n est congru à 1 modulo 5. - Si D est égal à 1, cela signifie que n n'est pas congru à 1 modulo 5. Finalement, le PGCD de a et b est égal à 5 si et seulement si n est congru à 1 modulo 5, et il est égal à 1 si et seulement si n n'est pas congru à 1 modulo 5.