Cours d'apprentissage en ligne

Racine rationnelle de polynôme

Dans cet exercice, nous devons montrer qu'un polynôme admet une racine rationnelle. Pour cela, nous devons prouver que si P/Q est une racine de F, alors P divise 3 et Q divise 2. Nous commençons par écrire F(P/Q) de manière simplifiée en évitant les fractions. Après quelques simplifications, nous obtenons l'équation 2P^3 + 5P^2Q + 5PQ^2 + 3Q^3 = 0 (équation 1). Pour montrer que P divise 3, nous factorisons l'équation 1 par P et observons que P divise -3Q^2. Étant donné que le PGCD de P et Q vaut 1, nous pouvons conclure que P divise 3, conformément à ce qui était demandé. De même, en factorisant l'équation 1 par Q, nous montrons que Q divise 2P^3, et nous pouvons conclure que Q divise 2. Ainsi, nous avons répondu à la première question. Dans la deuxième question, nous devons déduire que F admet une racine rationnelle. Pour cela, nous savons que si une racine rationnelle existe, le numérateur doit diviser 3 et le dénominateur doit diviser 2. En utilisant les possibilités trouvées précédemment pour P et Q, nous testons les 8 combinaisons possibles. Après calculs, nous trouvons que la seule racine rationnelle est -3/2. Cela conclut l'exercice.

Décomposition en facteurs premiers

Dans cet exercice, nous cherchons les couples d'entiers (A, B) qui satisfont l'équation 3 * (21^A) = 14 * (9^B). Pour résoudre ce problème, nous utilisons la décomposition en facteurs premiers. En effet, afin d'identifier les puissances dans le produit, nous devons décomposer l'équation en facteurs premiers. La décomposition en facteurs premiers d'un nombre est unique, donc la décomposition de 3 * (21^A) est identique à celle de 14 * (9^B). Nous commençons par la partie gauche de l'équation, en décomposant 3 et en nous concentrant sur (21^A). Nous décomposons ainsi (21^A) en 3 * (7^A). Puis, nous utilisons les règles de calcul des puissances pour obtenir (3^A) * (7^A) à partir de (3 * (7^A)). En réorganisant le calcul de base, nous obtenons (3^(A+1)) * (7^A) pour 3 * (21^A). Ainsi, nous avons décomposé 3 * (21^A) de manière unique en (3^(A+1)) * (7^A). Nous faisons la même décomposition pour la partie droite de l'équation. En décomposant 14, nous obtenons 2 * 7. Et en décomposant 9, nous obtenons 3^2. Utilisant ensuite la règle de calcul des puissances, nous obtenons 2 * (3^(2B)) * 7^B pour 14 * (9^B). Pour que les deux produits soient identiques, nous devons trouver des valeurs de A et B qui satisfont cette équation. Cependant, le problème est que le facteur 2 apparaît dans la décomposition de 14 * (9^B), mais n'apparaît pas dans la décomposition de 3 * (21^A). Étant donné qu'A et B concernent le 3 (éventuellement le 7 aussi), mais pas le 2, nous ne pouvons pas compenser le facteur 2 avec A ou B. Par conséquent, il n'y a aucune valeur de A et B qui vérifie cette équation. Ainsi, nous concluons que l'équation n'a pas de solution.

Critère d'arrêt : n est premier ?

Dans cet exercice, nous utilisons le critère d'arrêt pour déterminer si un nombre est premier ou non. Le critère d'arrêt stipule que si un nombre n'est pas premier, il a un diviseur premier P compris entre 2 et la racine carrée de ce nombre. Nous n'avons pas besoin de tester tous les nombres premiers jusqu'au nombre que nous voulons tester pour savoir s'ils le divisent ou non. Nous devons simplement les tester jusqu'à la racine carrée de n. Dans cet exercice, nous calculons la racine carrée de 349, ce qui donne environ 18,7. Par conséquent, nous devons tester tous les nombres premiers inférieurs ou égaux à 18,7. Nous nous arrêtons à 17, ce qui signifie que nous devons tester si 2, 3, 5, 7, 11, 13 et 17 divisent 349. Ces nombres premiers doivent être connus, puisqu'ils sont utilisés régulièrement dans les exercices. En testant ces nombres, nous constatons rapidement qu'aucun d'entre eux ne divise 349. Par conséquent, nous concluons que 349 est un nombre premier. Cela conclut l'exercice sur l'utilisation du critère d'arrêt.

Démo infinité des premiers

Dans cet exercice, nous allons montrer qu'il existe une infinité de nombres premiers. Pour cela, nous supposons que l'ensemble des nombres premiers est fini, et nous allons parvenir à une contradiction. Nous commençons par noter P comme étant l'ensemble des nombres premiers, et nous supposons qu'il contient N nombres, notés P1, P2, P3... jusqu'à PN. Nous construisons ensuite un nouveau nombre appelé P étoile, qui est le produit de tous les nombres premiers de l'ensemble P, auquel nous ajoutons 1. La première étape consiste à montrer que pour chaque indice i appartenant à N, le nombre Pi ne divise pas P étoile. Nous utilisons une démonstration par l'absurde et supposons qu'il existe un indice i pour lequel Pi divise P étoile. Cependant, P étoile est congru à 1 modulo Pi, ce qui contredit le fait que Pi divise P étoile. Ainsi, aucun nombre premier de l'ensemble P ne divise P étoile. Ensuite, nous montrons que P étoile est strictement plus grand que le plus grand des nombres premiers de l'ensemble P. Par conséquent, P étoile ne peut pas être un nombre premier. Cependant, selon le critère d'arrêt, il existe un nombre premier Pi dans l'ensemble P qui divise P étoile. Cela contredit ce que nous avons prouvé dans la première étape, où nous avons montré qu'aucun nombre premier de l'ensemble P ne divise P étoile. Cette contradiction prouve que notre supposition selon laquelle l'ensemble des nombres premiers est fini est fausse. Par conséquent, il existe une infinité de nombres premiers. Cela conclut l'exercice.

Décomposition et équation

Dans cet exercice, nous devons résoudre l'équation x(x+1)(2x+1) = 84 pour trouver les solutions entières. Pour cela, nous commençons par décomposer 84 en facteurs premiers, ce qui nous donne 2^2 * 3 * 7. Ensuite, nous examinons toutes les possibilités d'écrire 84 comme un produit de 3 facteurs distincts, en tenant compte du fait que x, x+1 et 2x+1 doivent tous être différents. Nous constatons que 2*6*7 n'est pas une option car 2x+1 serait plus petit que x+1. En revanche, 2*3*14 et 3*4*7 sont des options valides. En analysant chaque possibilité, nous trouvons que seule la deuxième option fonctionne, avec x=3. Ainsi, la solution de l'équation dans ce cas est x=3.

Nombre de diviseurs

Dans cet exercice, nous devons compter le nombre de diviseurs du nombre 300 puissance 300. Pour cela, nous devons décomposer 300 puissance 300 en facteurs premiers, puis conclure avec le nombre de diviseurs de ce nombre. Nous commençons par remarquer que 300 est égal à 3 fois 10, ce qui est équivalent à 3 fois 2 au carré fois 5 au carré. En élevant cela à la puissance 300, nous obtenons 3 puissance 300 fois 2 au carré fois 5 au carré puissance 300. En distribuant la puissance dans le produit, nous obtenons 3 puissance 300, 2 au carré fois 300 et 5 au carré fois 300. Il s'agit de puissances de puissance, donc nous multiplions les exposants, ce qui donne 2 puissance 600 et 5 puissance 600. Maintenant, pour déterminer le nombre de diviseurs, nous utilisons une formule : si nous avons la décomposition en facteurs premiers d'un nombre n égale à p1 puissance alpha 1 fois p2 puissance alpha 2, etc., alors le nombre de diviseurs est égal à (alpha 1 + 1) fois (alpha 2 + 1), etc. En utilisant cette formule, nous prenons toutes les puissances et nous leur ajoutons 1, puis nous multiplions tout cela. Dans le cas de 300 puissance 300, nous avons 301 fois 601 fois 601 diviseurs, ce qui donne un total de 108 721 501 diviseurs. Maintenant, pour la deuxième question qui demande de trouver un nombre ayant plus d'un milliard de diviseurs, nous remarquons que nous sommes déjà très proches avec 108 721 501 diviseurs. Nous devons juste trouver un moyen de multiplier ce nombre par 10 pour atteindre le milliard. En prenant par exemple la puissance 9, cela ajoute 10 diviseurs (puisque 9 + 1 = 10). En multipliant tous les diviseurs par 10 dans la formule, nous atteignons le milliard de diviseurs pour 300 puissance 300 fois 7 puissance 9.

Utiliser Fermat 1/2

Dans cet exercice, nous devons démontrer que, pour tout nombre premier P différent de 3 et tout nombre naturel n, l'expression 3^n + P - 3^(n+1) est divisible par P. Nous allons utiliser le théorème de Fermat pour résoudre cet exercice. Le théorème de Fermat stipule que, si A est un nombre entier et P est un nombre premier qui ne divise pas A, alors A^P - 1 est congru à 1 modulo P. Nous voulons montrer que 3^n + P - 3^(n+1) est congru à 0 modulo P. Pour cela, nous allons voir si nous pouvons utiliser le théorème de Fermat. Dans l'énoncé, il est précisé que nous avons un nombre premier différent de 3. Étant donné que P est premier et différent de 3, cela signifie simplement que P ne divise pas 3. Par conséquent, nous pouvons appliquer le théorème de Fermat avec 3 et P. D'après le petit théorème de Fermat, nous avons 3^P - 1 est congru à 1 modulo P. Maintenant, nous allons utiliser ce résultat. Nous voulons faire apparaître les puissances 3^(n+P) et 3^(n+1). Nous allons donc multiplier cette congruence par 3^(n+1). Avant cela, nous allons tout passer d'un côté pour obtenir 0. Donc, en multipliant par 3^(n+1), nous obtenons 3^(n+1) * (3^P - 1) - 3^(n+1). Maintenant, nous avons obtenu la puissance que nous recherchions, à savoir 3^(n+1). Et comme nous avons deux puissances de 3 différentes en produit, nous additionnons les exposants. Donc, cela devient (n+1) + (P-1) = n + P. Finalement, nous avons démontré que 3^n + P - 3^(n+1) est congru à 0 modulo P.

Utiliser Fermat 2/2

Le petit théorème de Fermat est utilisé pour montrer que pour tout nombre premier P et nombre entier A qui n'est pas divisé par P, A puissance P moins 1 est divisible par P. Dans le premier exercice, on montre que 4 puissance 28 moins 1 est divisible par 29 en appliquant le petit théorème de Fermat. Dans le deuxième exercice, on montre que pour tout n, 4 puissance n moins 1 est divisible par 3 en utilisant les congruences et en remarquant que 4 est congru à 1 modulo 3. Dans le troisième exercice, on montre que pour tout k, 4 puissance 4k moins 1 est divisible par 5 et par 17, en utilisant les congruences et en remarquant que 4 puissance 4 est congru à 1 modulo 5 et modulo 17. Enfin, dans la dernière question, on déduit que 4 puissance 28 moins 1 a quatre diviseurs premiers, à savoir 3, 5, 17 et 29, en utilisant les résultats précédents.

Vers la sup : racine puissance n

Dans cet exercice, nous utilisons le théorème de Bézout pour calculer différentes expressions. Nous commençons par calculer 1 plus la racine carrée de 6 au carré, 1 plus la racine carrée de 6 puissance 4 et puissance 6, en utilisant les identités remarquables et les calculs simples. Ensuite, nous décomposons en facteurs premiers les nombres obtenus et observons qu'ils sont premiers entre eux, car ils n'ont aucun diviseur commun. Ensuite, nous généralisons ces calculs en utilisant n au lieu de carré, 4 ou 6, et nous trouvons les valeurs de an et bn correspondantes. Nous calculons également an plus 1 et bn plus 1 en fonction de an et bn, en appliquant les règles de calcul des puissances. Enfin, nous démontrons que si 5 ne divise pas an plus bn, alors 5 ne divise pas non plus an plus 1 et bn plus 1, en utilisant la contraposée. Nous utilisons les propriétés de la somme de deux nombres divisibles par 5 pour montrer que si 5 divise an plus 1 et bn plus 1, alors il divise également an plus bn. En conclusion, nous démontrons que si an et bn sont premiers entre eux, alors an plus 1 et bn plus 1 sont également premiers entre eux. Nous concluons également que les valeurs de an et bn trouvées précédemment sont toujours premières entre elles. L'exercice se termine en expliquant que ces résultats sont généralisables et en prouvant qu'ils sont vrais pour tous les n.

Congruence : équation degré 2

Dans cet exercice, nous devons résoudre l'équation x²-2x+2≡0 (mod 17) en utilisant l'équation du second degré en congruence. Tout d'abord, nous devons montrer que α=5 est une solution de l'équation E. En remplaçant x par 5, nous obtenons 25-10+2=17, qui est congruent à 0 modulo 17. Donc, α est bien une solution de E. Ensuite, nous posons x̄=x-α pour trouver toutes les solutions de E. En remplaçant x par x̄+α dans l'équation E, nous obtenons (x̄+α)²-2(x̄+α)+2≡0 (mod 17). En développant l'équation, nous obtenons x̄²+8x̄≡0 (mod 17). Nous factorisons l'équation en utilisant la congruence à 0 modulo 17, ce qui nous donne x̄(x̄+8)≡0 (mod 17). Selon le lemme de Gauss, puisque 17 est premier et qu'il divise le produit, il divise soit x̄ soit (x̄+8). Nous avons donc deux possibilités à étudier : 1) Si 17 divise x̄, cela signifie que x≡5 (mod 17). 2) Si 17 divise (x̄+8), cela signifie que x≡14 (mod 17). Ainsi, toutes les solutions de E sont x≡5 (mod 17) ou x≡14 (mod 17).

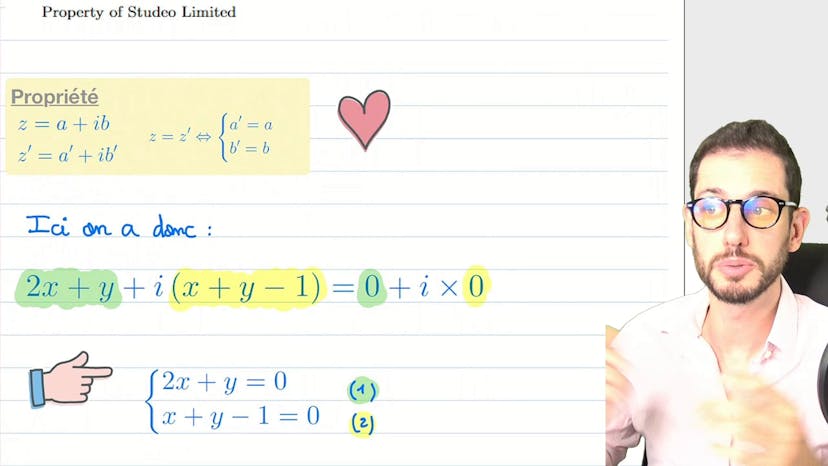
Partie réelle et imaginaire

Un nombre complexe est composé d'une partie réelle et d'une partie imaginaire, et s'écrit généralement sous la forme Z = A + iB. Pour résoudre une équation avec des nombres complexes, on peut utiliser une méthode classique en identifiant les deux complexes. Les complexes ont deux dimensions, la partie réelle et la partie imaginaire. L'équation donne 2X + Y comme partie réelle et X + Y - 1 comme partie imaginaire. On peut écrire cette équation sous forme de système en mettant les deux parties égales à 0. Après avoir résolu le système, on trouve X = -1 et Y = 2. Cette méthode permet d'identifier les solutions d'une équation complexe.