Cours d'apprentissage en ligne

Savoir-faire : les médiatrices

En géométrie, on peut repérer un point de deux manières. La première consiste à utiliser ses coordonnées (abscisse et ordonnée), ce qui correspond au complexe A + B. La deuxième manière est d'utiliser sa distance par rapport à l'origine et l'angle qu'il forme avec l'axe des abscisses. Cette méthode permet de trouver un point unique. La norme du vecteur OM est équivalente au module du complexe Z associé et l'angle entre le vecteur OM et l'axe OX est appelé l'argument de Z. On peut représenter une distance AB comme la différence entre deux nombres complexes (ZB - ZA). Un concept important à retenir est que lorsque vous devez trouver l'ensemble des points vérifiant une relation, il est possible de traduire cela en termes de distances et d'utiliser des complexes pour trouver la médiatrice ou le cercle correspondant. Si vous avez une relation du type Z - ZA = Z - ZB, vous savez que les points correspondants sont sur la médiatrice de AB. Cette technique est très courante et doit être maîtrisée. Il est important de reconnaître ces situations dès le départ et de ne pas les redécouvrir à chaque fois.

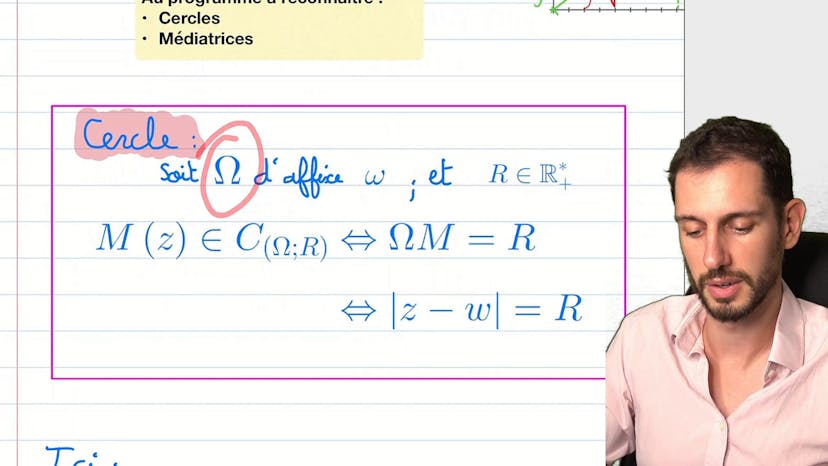
Savoir-faire : les cercles

Dans ce cours, nous avons discuté de la représentation des points dans le plan en utilisant des coordonnées polaires. On a vu qu'un point peut être défini à la fois par sa distance à l'origine et son angle avec l'axe des abscisses. Cette représentation peut être traduite en utilisant des nombres complexes, où la norme correspond à la distance du point à l'origine et l'argument correspond à l'angle avec l'axe des abscisses. Nous avons également abordé la notion de cercle et sa définition mathématique. Un cercle est l'ensemble des points équidistants d'un point fixe, appelé centre du cercle. On peut traduire cette définition en utilisant des nombres complexes en exprimant la distance entre un point du cercle et le centre en tant que module du nombre complexe correspondant. Ensuite, nous avons discuté de la manière de reconnaître des équations qui décrivent des cercles dans le plan. Une équation de la forme module de z plus d'autres termes égal à une constante peut être associée à un cercle, où z est un nombre complexe représentant un point du cercle. Finalement, nous avons vu un exemple où une équation module de z plus d'autres termes égal à 4 était donnée. En réarrangeant l'équation et en choisissant un point arbitraire comme centre du cercle, on a pu conclure que les points satisfaisant cette équation appartenaient au cercle de centre -7-2i et de rayon 4. J'espère que cela a été clair. N'hésitez pas à poser des questions si nécessaire, et à bientôt dans une prochaine vidéo.

Forme expo 1 : méthode type

Dans cette vidéo, nous cherchons à trouver la forme exponentielle de 2-2i en utilisant la méthode classique. Nous commençons par trouver z, puis nous factorisons pour faire apparaître cosθ plus i sinθ. Le module de z est calculé en utilisant la formule √a2 plus b2, ce qui nous donne 2√2. Ensuite, nous factorisons 2-2i par 2√2, ce qui donne 1 sur √2 moins i fois 1 sur √2. Pour éliminer les racines au dénominateur, nous multiplions en haut et en bas par √2, ce qui nous donne √2 sur 2 moins i√2 sur 2. Nous remarquons que cette forme correspond à un angle classique, π sur 4. Cependant, nous remarquons également un signe négatif, ce qui indique que l'angle est en réalité -π sur 4. Nous pouvons donc réécrire 2-2i sous la forme cos -π sur 4 plus i sin -π sur 4. En conclusion, la forme exponentielle de 2-2i est cos -π sur 4 plus i sin -π sur 4. Dans la prochaine vidéo, nous verrons une méthode plus astucieuse pour résoudre ce problème.

Forme expo 2 : + rapide

Dans cette transcription vidéo, l'enseignant aborde deux méthodes pour résoudre des exercices sur les nombres complexes. La première méthode est la méthode classique, où l'on calcule le module de l'élément complexe et on factorise le nombre pour trouver la forme cosθ plus sinθ. La deuxième méthode, plus astucieuse, consiste à utiliser des valeurs d'angles classiques très couramment utilisées dans les exercices de lycée et de mathématiques supérieures. Ces angles courants sont π sur 6, π sur 4 et π sur 3. L'enseignant conseille de les apprendre par cœur, ainsi que la forme algébrique et trigonométrique exponentielle correspondante. En utilisant cette méthode astucieuse, l'enseignant explique comment résoudre rapidement des exercices en reconnaissant les nombres complexes courants et leur forme trigonométrique exponentielle. L'enseignant encourage également les élèves à bien maîtriser les formules et à savoir les reconnaître, car une fois cela acquis, cela permet de résoudre les exercices plus rapidement. Il précise toutefois que dans les premières séances ou les premiers contrôles, il est préférable de suivre la méthode classique pour bien comprendre le processus. En conclusion, l'enseignant souligne l'importance d'apprendre et de reconnaître les nombres complexes courants en forme trigonométrique exponentielle pour résoudre les exercices plus efficacement. Note: Le résumé a été rédigé en gardant à l'esprit les bonnes pratiques de référencement pour les moteurs de recherche (SEO friendly).

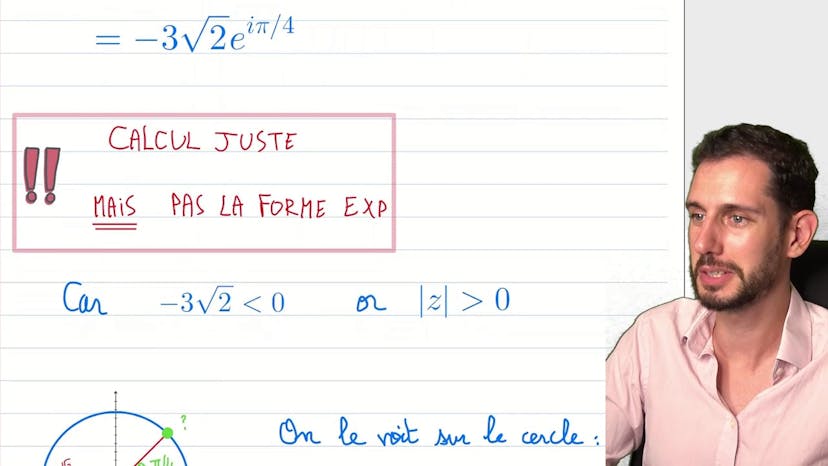
Forme expo 3 : erreur type !

Dans ce cours, il est expliqué comment résoudre des exercices sur les nombres complexes. L'auteur met en garde contre les pièges et les erreurs fréquentes, notamment en ce qui concerne la forme exponentielle d'un nombre complexe. Il explique qu'il faut faire attention à utiliser la bonne formule, qui est le module du nombre complexe multiplié par l'exponentielle de l'argument, et non pas simplement l'exponentielle de l'argument. L'auteur utilise un exemple pour illustrer son propos. Il présente un nombre complexe de la forme -3 + 3i et explique comment le calculer en utilisant la forme exponentielle. Il montre que la forme correcte est en réalité 3√2 * e^(iπ/4). Pour éviter les erreurs, l'auteur propose une astuce : lorsqu'il y a un moins devant un nombre complexe, il peut être remplacé par l'exponentielle de l'angle pi. Cela permet d'obtenir la bonne forme exponentielle sans perdre de points lors d'un contrôle. En conclusion, l'auteur recommande de faire attention aux erreurs fréquentes dans les exercices sur les nombres complexes et propose une astuce pour éviter de perdre des points en utilisant la bonne forme exponentielle.

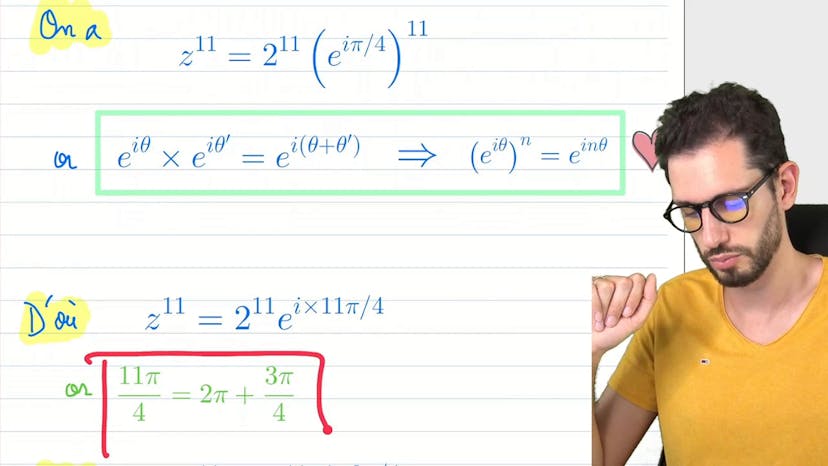
Forme expo → algébrique

Dans cette vidéo, on utilise la forme exponentielle pour trouver la forme algébrique de z puissance 11. On pose z égale à 2EI pi sur 4. On écrit z puissance 11 en forme exponentielle en utilisant les formules de l'exponentielle complexe. On utilise la propriété de l'exponentielle complexe qui dit que E2Iθ puissance n est égal à E2Inθ. On fait rentrer le 11 dans le Ipi sur 4 pour obtenir z puissance 11 égale à 2 puissance 11 fois E2I11pi sur 4. On remarque que les puissances de l'exponentielle complexe ajoutent des angles et parfois font des tours complets autour du cercle. On remarque que 11pi sur 4 est proche de 12pi sur 4 qui est égal à 3pi. On exprime 11pi sur 4 comme 8pi sur 4 plus 3pi sur 4. On peut alors remplacer 11pi sur 4 par 2pi sur 11 cos 3pi sur 4 plus i sin 3pi sur 4. On simplifie cette expression et on obtient la forme algébrique de z puissance 11 égale à 2 puissance 10 racine de 2 fois moins 1 plus i. La partie réelle est 2 puissance 10 racine de 2 fois moins 1 et la partie imaginaire est 2 puissance 10 racine de 2. On utilise les propriétés de l'exponentielle complexe pour trouver le bon angle et les différentes rotations nécessaires pour obtenir les valeurs du cosinus et du sinus.

Classique : trouver un cos

Ce cours aborde le sujet des nombres complexes et la manière de les exprimer sous différentes formes, à savoir la forme algébrique et la forme exponentielle. L'objectif est de trouver une expression algébrique de cos(pi/12), en utilisant les propriétés des complexes. Pour y parvenir, on utilise les relations connues entre les angles tels que pi/2, pi/3, pi/4, etc. On fait alors une remarque cruciale : pi/12 peut être exprimé comme (pi/3) - (pi/4). Grâce aux propriétés de l'exponentielle, on peut exprimer E^(2i(pi/12)) comme E^(2i(pi/3)) * E^(-2i(pi/4)), ce qui permet ensuite de l'exprimer en forme algébrique. En effectuant les calculs nécessaires, on obtient les valeurs de la partie réelle et de la partie imaginaire de E^(2i(pi/12)), qui correspondent respectivement à cos(pi/12) et sin(pi/12). Ainsi, on peut exprimer cos(pi/12) en forme algébrique.

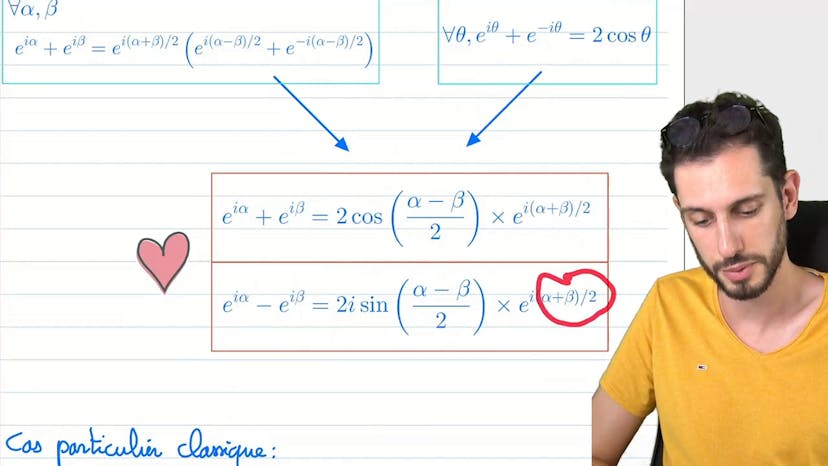
Astuce : angle moitié

Ce cours présente une méthode pour résoudre un exercice de mathématiques qui implique des nombres complexes. L'objectif est de trouver une forme exponentielle pour l'expression Z + Z' et Z - Z'. Pour cela, il est recommandé de factoriser les expressions en utilisant une astuce appelée "factorisation par l'angle moitié". Cette astuce consiste à créer une expression contenant un nombre et son conjugué, ce qui permet d'obtenir une forme plus simple. Ensuite, il est possible d'utiliser cette forme factorisée pour résoudre des équations ou résoudre des problèmes. Il est important de vérifier la positivité des angles pour trouver la forme exponentielle correcte. En résumé, il s'agit de factoriser les expressions, utiliser la formule de la somme ou de la différence des exponentielles, et vérifier la positivité des angles pour obtenir la forme exponentielle correcte.

Linéariser cos³ !

Dans ce cours, l'objectif est de trouver une expression pour cos3θ en fonction de cos2θ. Pour cela, on utilise la formule de Moivre : E2iθ³ = cos3θ + isin3θ. On sait que la partie réelle de E2iθ³ est cos3θ, ce qui nous intéresse. On utilise ensuite la formule du binôme de Newton pour développer (cosθ + isinθ)³ et identifier les termes ayant une partie réelle intéressante. On obtient ainsi cos3θ = cos³θ - 3cosθsin²θ. Pour se débarrasser du sin²θ, on utilise la formule trigonométrique fondamentale cos²θ + sin²θ = 1. En remplaçant sin²θ par 1-cos²θ, on obtient finalement cos3θ = 4cos³θ - 3cosθ. Ainsi, on a isolé cos³θ en fonction de cosθ. Cette méthode d'identification et de manipulation des expressions est très courante en mathématiques.

Inégalité triangulaire, partie réelle et imaginaire d’un quotient

Dans ce cours, Paul aborde plusieurs questions sur les complexes. Pour la première question, il utilise l'inégalité triangulaire pour établir une inégalité. Pour la deuxième question, il explique comment exprimer la partie réelle et la partie imaginaire de A sur B en fonction des parties réelles et imaginaires de A et B, ainsi que du module de B. Paul suggère d'utiliser les formules qui lient partie réelle, partie imaginaire, module, et le nombre et son conjugué. Ensuite, il calcule les parties réelles et imaginaires de 1+Eialpha et 1+Eibêta. Il fait également référence à la formule de l'air pour simplifier les calculs. Il note que cette formule est très utile dans les problèmes complexes et encourage à la retenir. En conclusion, Paul résume les résultats obtenus et donne quelques conseils pour mieux visualiser les angles complexes. Il termine en soulignant l'importance de comprendre les formules de l'air.

Équations polynomiales

Dans cette vidéo, Paul explique comment résoudre des équations du second degré à coefficient complexe. La technique pour résoudre ces équations est similaire à celle des équations en réel. Les solutions de l'équation AZ² + BZ + C = 0 sont Z1 = (-B - √Δ)/2A et Z2 = (-B + √Δ)/2A, où Δ = B² - 4AC. Paul résout une première équation avec A = 1, B = 1 et C = 1, et obtient les solutions Z1 = 1 + i et Z2 = 1 + 2i. Ensuite, Paul aborde une deuxième équation déguisée en équation du second degré en utilisant la substitution X = Z3. Il résout l'équation du second degré en X et trouve Δ = -15 - 8i. Pour trouver la racine carrée de Δ, il pose Δ = a + ib et utilise l'équation Δ² = Δ, ce qui donne les équations sur la partie réelle et la partie imaginaire de Δ. En résolvant ces équations, il obtient A = 1 et B = -4, ou A = -1 et B = 4. Les solutions de cette deuxième équation sont x1 = 1 - i et x2 = 3i. Cependant, Paul souhaite maintenant trouver les solutions pour l'équation originale. Il résout l'équation E1 en écrivant Z3 = 1 - i ou Z3 = 3i, sous forme exponentielle. Il utilise la racine 1ère de l'unité pour résoudre cette équation et obtient six solutions au total. Il conclut en disant que cela est cohérent avec le fait que le polynôme de départ était de degré 6. Ce résumé explique comment résoudre des équations du second degré à coefficient complexe et décrit les étapes suivies par Paul pour résoudre deux exemples spécifiques.