Cours d'apprentissage en ligne

Cardinal de l’univers

Dans cet exercice de Proba, on considère un univers fini ω avec n événements indépendants a1, a2, ..., an. Ces événements sont liés à de nouveaux événements b1, b2, ..., bn, qui appartiennent aux partitions de l'univers et satisfont la condition que chaque bk est soit égal à ak, soit au complémentaire de ak. On commence par montrer que l'intersection de tous les bn est non vide. Les événements bk étant indépendants, la probabilité de leur intersection est le produit de leurs probabilités. Comme les probabilités des bk sont différentes de zéro, le produit des n nombres non nuls est non nul. Donc, l'intersection est non vide. Ensuite, on démontre que si on prend deux éléments bn et bn' avec nk différent de nk', alors leur intersection est l'ensemble vide. Comme les probabilités des bn sont différentes de zéro, il existe un k tel que bk est différent de bk'. Et comme bk est soit ak, soit le complémentaire de ak, on a donc une intersection vide entre bn et bn'. Finalement, on utilise ces résultats pour montrer que le cardinal de l'univers Omega est supérieur ou égal à 2^n. On a montré que pour chaque élément bn, il existe un élément x dans bn. De plus, les éléments xb dans les différents bn sont tous différents. Comme pour chaque bn, il y a deux possibilités (ak ou complémentaire de ak), le nombre total d'éléments xb est au moins 2^n. Donc, le cardinal de Omega est supérieur ou égal à 2^n.

Indicatrice d’Euler

Dans cet exercice de mathématiques portant sur les probabilités, nous avons un entier N strictement supérieur à 1. On choisit de manière équiprobable un entier X parmi les entiers compris entre 1 et N. Les AM sont les événements où M est inférieur ou égal à N et divise X. B est l'événement où X est premier avec N. Pour la première question, nous devons exprimer B en fonction des APK. Si X est premier avec N, cela signifie qu'aucun PK ne divise X. Ainsi, B est l'intersection de tous les complémentaires de AP1, AP2, ..., APR. Ensuite, pour tout entier naturel M qui divise N, nous devons calculer la probabilité de AM. P de AM est égal au nombre de multiples de M plus petits que N, divisé par le nombre total d'entiers entre 1 et N. Nous devons également montrer que les événements AP1, AP2, ..., APR sont mutuellement indépendants. Pour cela, nous prenons K entiers distincts parmi les nombres premiers de N. Le produit des probabilités de ces événements est égal à la probabilité de leur intersection, car les PIJ sont premiers entre eux. En déduire la probabilité de B est simple puisque les événements sont indépendants. La probabilité de B est le produit des complémentaires des probabilités de chaque AP. Enfin, nous notons Phi de N comme l'indicatrice d'air, c'est-à-dire le nombre d'entiers compris entre 1 et N qui sont premiers avec N. Nous voulons montrer que Phi de N est égal à N fois le produit de 1 moins chaque PK, pour K allant de 1 à R. Nous utilisons l'équiprobabilité et la probabilité de B pour montrer cela. Voilà pour le résumé SEO friendly de cet exercice sur les probabilités !

Schéma de Bernoulli

La loi binomiale permet de calculer les probabilités dans des situations où il y a répétition indépendante d'une expérience avec deux résultats possibles : succès ou échec. Pour utiliser cette loi, il faut suivre quelques étapes. Tout d'abord, repérer un chemin de Bernoulli, c'est-à-dire une expérience répétée plusieurs fois indépendamment. Ensuite, attribuer une variable aléatoire x qui représente le nombre de succès. Cette variable suit une loi binomiale de paramètres n et p, où n est le nombre de répétitions et p est la probabilité de succès. Pour calculer la probabilité que x soit égal à k, on utilise la formule suivante : k parmi n fois p à la puissance k, multiplié par 1 moins p à la puissance n moins k. Appliquons ces étapes à un exemple concret. Supposons que nous effectuons des tirages successifs et indépendants de boules, et que notre succès est de tirer une boule noire. Le paramètre de la loi binomiale est alors de 3 boules noires sur 8 boules, ce qui équivaut à une probabilité de réussite de 3/8. En appelant x le nombre de boules noires obtenues, x suit une loi binomiale de paramètres n égal à 5 (car nous faisons 5 tirages) et p égal à 3/8. En utilisant la formule, nous pouvons calculer la probabilité que x soit égal à 3 : 3 parmi 5 fois (3/8) à la puissance 3, multiplié par 1 moins (3/8) à la puissance 5 moins 3. Les calculs nous donnent une probabilité de 20%. C'est ainsi que l'on reconnaît et utilise la loi binomiale pour effectuer des calculs de probabilité. Si vous avez des questions supplémentaires, consultez la FAQ.

Calcul brut de probabilités

Dans ce cours, nous allons effectuer les premiers calculs avec la loi binomiale. Pour cela, nous avons besoin d'une calculatrice. Nous avons une loi binomiale avec un grand X qui suit la loi de paramètre n égal à 50 et p égal à 0,23. Nous devons calculer trois probabilités. La première probabilité consiste à trouver la probabilité que p soit strictement inférieur à 12, ce qui est équivalent à la probabilité que x soit inférieur ou égal à 11. Ce résultat peut être obtenu sur toutes les calculatrices graphiques du lycée. En utilisant la calculatrice, nous obtenons le résultat de 0,512. Si vous n'avez pas de calculatrice, nous ne vous poserions pas cette question ici. Cependant, dans l'absolu, vous devriez faire la somme des p de x égal à 1, plus p de x égal à 2, etc. jusqu'à p de x égal à 11, ce qui serait fastidieux. La deuxième probabilité demande de trouver la probabilité que x soit supérieur ou égal à 4. Nous pouvons considérer l'événement contraire, c'est-à-dire l'événement où x est inférieur ou égal à 3. En utilisant la calculatrice, nous obtenons le résultat de 0,999. Enfin, la troisième probabilité consiste à trouver la probabilité que x soit compris entre 5 et 8. Cela équivaut à la différence entre la probabilité que x soit inférieur ou égal à 8 et la probabilité que x soit inférieur ou égal à 5. En utilisant la calculatrice, nous obtenons le résultat de 0,14. Une autre méthode qui fonctionnerait également serait d'additionner les probabilités de x égal à 6 et de x égal à 7, qui donne également 0,14. Il est important de s'assurer que vous connaissez la bonne fonction sur votre calculatrice. Vous pouvez demander à vos camarades, consulter la FAQ de votre modèle de calculatrice ou rechercher sur Google pour trouver cette information. Les trois méthodes fonctionnent.

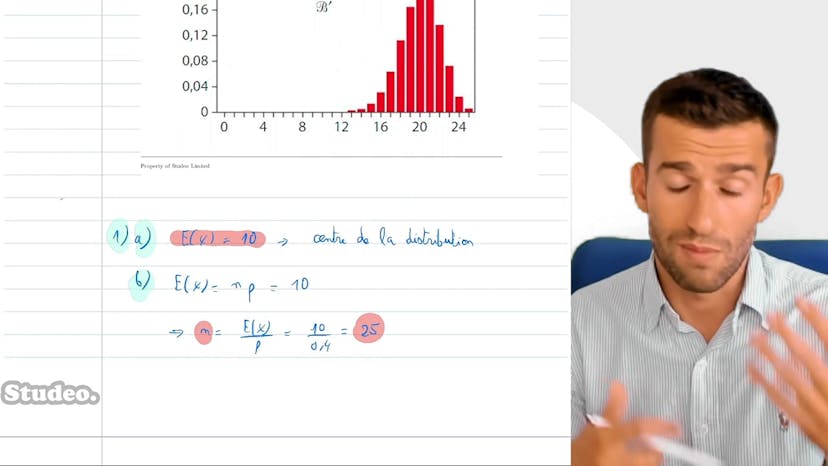
Espérance et écart-type : graphique

Dans ce cours, nous étudions l'utilisation des diagrammes en barres pour les lois binomiales. Nous commençons par un exemple où la probabilité de succès (P) est connue à 0,4, mais nous ne connaissons pas la valeur de N. Pour estimer l'espérance, nous devons prendre en compte que la loi binomiale n'est symétrique que lorsque P est égal à 0,5. Cependant, nous pouvons estimer que N est centré autour de 10, en supposant qu'il s'agit d'une valeur entière. Donc, l'espérance (E2x) serait d'environ 10. En utilisant cette information, nous pouvons calculer une valeur possible pour N en utilisant la formule N = E2x/P, ce qui donne 25 pour ce cas précis. Ensuite, nous étudions une deuxième loi binomiale et nous devons la comparer à la première. Nous pouvons observer que la deuxième loi est plus recentrée et moins étalée que la première. L'écart-type mesure la dispersion des valeurs par rapport à la moyenne. Une plus petite valeur d'écart-type indique une plus faible dispersion des valeurs par rapport à la moyenne. Les concepts importants à retenir sont l'espérance (NxP), la variance (NPx-P) et l'écart-type (la racine carrée de la variance). Dans le cas de la deuxième courbe, l'écart-type est plus faible, ce qui signifie que la variance (Px-P) est également plus faible. Ensuite, nous abordons un exercice supplémentaire qui consiste à trouver quelle valeur de P conduit à l'écart-type maximum. Pour cela, nous utilisons la fonction f2x = x*(1-x), qui est un problème de degré 2. En trouvant les racines de cette fonction, nous obtenons 0 et 1. L'extrême de cette fonction est atteint au milieu de ces deux racines, qui est à 1,5. En calculant la valeur de la fonction à ce point, nous obtenons 1,25. Donc, l'écart-type maximum est atteint lorsque la probabilité (P) est de 1,5. Cela s'explique par le fait que lorsque la probabilité est élevée, il y a autant de chances d'avoir des échecs que des réussites, ce qui peut entraîner des résultats très différents. Cet aparté supplémentaire nous montre comment lire des informations à partir d'un diagramme en barres. En conclusion, ce cours explique comment utiliser les diagrammes en barres pour analyser des lois binomiales, en estimant l'espérance et en comparant les différences d'écart-type entre les différentes lois.

Binomiale et tirage avec remise

La loi binomiale est utilisée pour modéliser des expériences avec une répétition de plusieurs essais indépendants, ayant deux résultats possibles. Pour reconnaître et utiliser cette loi, il faut identifier un schéma de Bernoulli, qui consiste en une répétition d'une même expérience, de façon indépendante et avec deux résultats possibles (échec ou réussite). Ensuite, il faut attribuer une variable aléatoire x pour représenter le nombre de succès. Cette variable suit une loi binomiale avec les paramètres n (nombre de répétitions) et p (probabilité de succès). La formule utilisée pour calculer la probabilité que x soit égal à k est donnée par "k parmi n" multiplié par p élevé à la puissance k, multiplié par (1 moins p) élevé à la puissance (n moins k). Dans l'exemple donné, il s'agit de tirages successifs et indépendants où le succès est de tirer une boule noire parmi huit boules, avec trois boules noires au total. Cela correspond à une épreuve de Bernoulli avec un paramètre de p égal à 3/8. La variable x, représentant le nombre de boules noires obtenues, suit donc une loi binomiale avec les paramètres n égal à 5 et p égal à 3/8. En appliquant la formule, on peut calculer la probabilité que x soit égal à 3, ce qui donne 20%. Pour plus d'informations, vous pouvez consulter la FAQ.

Classique : produit défectueux en usine

Ce cours concerne les produits défectueux en usine et leurs tests. On a une usine avec deux tests indépendants. La probabilité qu'un produit défectueux passe le premier test est de 0.12 et de 0.08 pour le deuxième test. Pour qu'un produit défectueux soit mis en vente, il doit passer les deux tests. La probabilité de vente est donc de 0.12 * 0.08 = 0.0096 (soit moins de 1%). Ensuite, on nous demande la probabilité qu'au moins trois produits défectueux soient mis en vente sur 100 produits indépendants. On utilise la loi binomiale avec comme paramètre 100 et une probabilité de vente de 0.0096. On calcule la probabilité complémentaire de moins de trois ventes, qui est égale à 1 moins la probabilité de 0, 1 et 2 ventes. On obtient 38% de chance de ne pas avoir de produit défectueux en vente, 36% de chance d'avoir un produit en vente défectueux et 18% de chance d'en avoir deux. La probabilité d'avoir trois ou plus de produits défectueux en vente est de 7%. Les formules utilisées sont les formules classiques de la loi binomiale : K parmi N, fois la probabilité à la puissance K, fois 1 moins la probabilité à la puissance N moins K.

Déterminer le + grand entier

Dans cette vidéo, Corentin aborde le sujet des variables aléatoires suivant des lois binomiales. Il cherche à déterminer le plus grand entier k tel que la probabilité que X soit supérieur ou égal à k soit supérieur ou égal à 0,9. Il explique que lorsque k augmente, la probabilité que X soit supérieur ou égal à k diminue car l'ensemble des valeurs de X supérieur ou égal à k devient de plus en plus petit. Son objectif est donc de trouver le cas où la probabilité que X soit supérieur ou égal à k+1 est strictement inférieure à 0,9, et que la probabilité que X soit supérieur ou égal à k est supérieur ou égal à 0,9. En utilisant sa calculatrice, il calcule la probabilité que X soit supérieur ou égal à 22 et obtient 0,80, ce qui ne correspond pas à sa recherche. En revanche, il remarque que la probabilité que X soit supérieur ou égal à 21 est de 0,89, et que la probabilité que X soit supérieur ou égal à 20 est de 0,95. Il conclut alors que le plus grand entier k tel que la probabilité que X soit supérieur ou égal à k soit supérieur ou égal à 0,9 est 20.

Déterminer le + petit entier

Dans cette vidéo, nous abordons la troisième méthode pour résoudre un problème de loi binomiale. L'énoncé nous demande de trouver le plus petit entier k tel que la probabilité que X soit inférieur ou égal à k soit supérieure ou égale à 0,5. La méthode utilisée est similaire à la méthode 2, mais cette fois-ci on raisonne à l'inverse. En effet, la probabilité que X soit inférieur ou égal à k augmente lorsque k augmente. Pour trouver la valeur de k, nous utilisons une calculatrice pour calculer les probabilités que X soit inférieur ou égal à un nombre décroissant jusqu'à trouver la probabilité souhaitée. Dans cet exemple, nous commençons avec k = 40 et trouvons que la probabilité que X soit inférieur ou égal à 40 est de 0,99, ce qui est trop élevé. Nous continuons à diminuer k et trouvons que la probabilité que X soit inférieur ou égal à 37 est de 0,96, ce qui se rapproche de notre objectif de 0,95. Finalement, nous trouvons que la probabilité que X soit inférieur ou égal à 36 est de 0,93, ce qui est inférieur à 0,95. Donc, nous concluons que la valeur de k est égale à 37.

Utiliser un arbre pondéré

Dans ce cours, nous utilisons un arbre pondéré pour calculer des probabilités d'événements. Nous avons des informations sur les probabilités et nous essayons d'en déduire d'autres. Nous savons que Naomi se rend au lycée en vélo ou en bus. Lorsqu'il fait beau, elle prend le vélo 8 fois sur 10, et quand il fait moche, elle prend le vélo 5 fois sur 10. De plus, il y a 75% de journées ensoleillées dans sa ville. Nous prenons une journée au hasard sans savoir s'il fait beau ou non, et nous voulons déterminer la probabilité que Naomi se rende en vélo (P de V) et la probabilité qu'elle se rende en vélo sachant qu'il fait beau (P de E inter V). Pour cela, nous construisons un arbre pondéré avec les branches "ensoleillé" ou "pas ensoleillé" et "vélo" ou "pas vélo". Nous déterminons les probabilités associées à chaque nœud en utilisant les informations données. Ensuite, nous calculons P de E inter V en utilisant la formule P de E x P de V sachant E (où E représente ensoleillé). Dans ce cas, il y a 60% de chance qu'il fasse beau et qu'elle prenne le vélo. Enfin, nous calculons P de V en utilisant la formule des probabilités totales, en considérant les chemins où Naomi prend le vélo. Dans ce cas, il y a 72.5% de chance qu'elle prenne le vélo. Cela résume les calculs de probabilités effectués à l'aide d'un arbre pondéré dans ce cours.

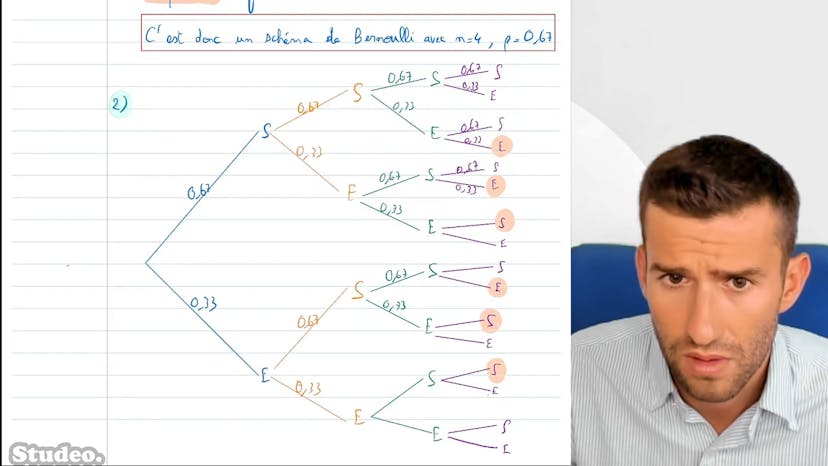
Représenter un schéma de Bernoulli

Dans ce cours, nous examinons le premier schéma de Bernoulli, qui concerne les probabilités d'achat de livres par les clients d'une librairie. On observe qu'il y a une probabilité de 67% pour qu'un client achète un livre lorsqu'il entre dans la librairie. Cette expérience est répétée avec quatre clients indépendants. Pour justifier que nous avons un schéma de Bernoulli, il faut vérifier certaines conditions : une même expérience répétée (achat ou non d'un livre), deux issues possibles (achat ou pas d'achat) et une indépendance entre les clients. Dans ce cas, nous avons bien un schéma de Bernoulli avec n égal à 4 (le nombre de clients) et p égal à 0,67 (la probabilité d'achat). Ensuite, nous devons construire un arbre pour représenter toutes les possibilités. Chaque branche de l'arbre représente soit un succès (achat d'un livre), soit un échec (pas d'achat). Chaque nœud de l'arbre a une probabilité de 67% de succès et 33% d'échec. Nous nous intéressons particulièrement au cas où deux clients sur les quatre achètent un livre. Grâce à l'arbre, nous pouvons repérer tous les chemins où il y a deux succès. Dans cet exemple, nous trouvons six chemins possibles. La probabilité que chaque chemin se produise est la même, car nous avons deux succès et deux échecs répartis de différentes manières. Donc, la probabilité que deux personnes achètent des livres est de 29%, calculée en utilisant les probabilités de succès et d'échec pour chaque chemin et en multipliant par le nombre de chemins possibles (6). Cette méthode permet de trouver directement les probabilités en lisant l'arbre. Cependant, nous verrons plus tard qu'il existe une formule plus systématique pour généraliser ce calcul avec la loi binomiale.

Analyse