Cours d'apprentissage en ligne

Encadrer sin(n)

Dans cette vidéo, nous allons étudier deux exemples de suites en utilisant les théorèmes de convergence. Le premier exemple concerne la suite u_n = n + 2 * sin(n). Nous devons montrer que pour tout entier n, u_n est supérieur à n - 2. Pour encadrer la fonction sinus, nous savons que le sinus est toujours compris entre -1 et 1. En multipliant par 2, nous obtenons une valeur positive. En ajoutant n, nous obtenons finalement que u_n est supérieur à n - 2. Bien que cette partie de l'inéquation ne soit pas importante, elle est vraie. Ce qui nous intéresse vraiment est le fait que u_n est supérieur à n - 2. Comme n - 2 tend vers plus l'infini, et que u_n est plus grand qu'une suite telle que n - 2, nous pouvons conclure que u_n tend vers l'infini. Le deuxième exemple concerne la suite v_n = -n^2 + (-1)^n. Encore une fois, nous devons encadrer la puissance (-1)^n, qui est toujours entre -1 et 1. Le terme (-1)^n n'aura pas beaucoup d'importance, car il va alterner entre -1 et 1. Le terme dominant est n^2, qui tend vers moins l'infini. En encadrant la suite, nous obtenons que v_n est inférieur à une suite qui tend vers moins l'infini. En factorisant le terme dominant, nous obtenons v_n = n^2 * (-(1/n) + 1/n^2). La partie à droite tend vers 1, et la partie à gauche tend vers moins 1. Donc v_n tend vers moins l'infini. En utilisant l'encadrement, nous avons montré que les deux suites étudiées tendent toutes les deux vers l'infini et moins l'infini, respectivement.

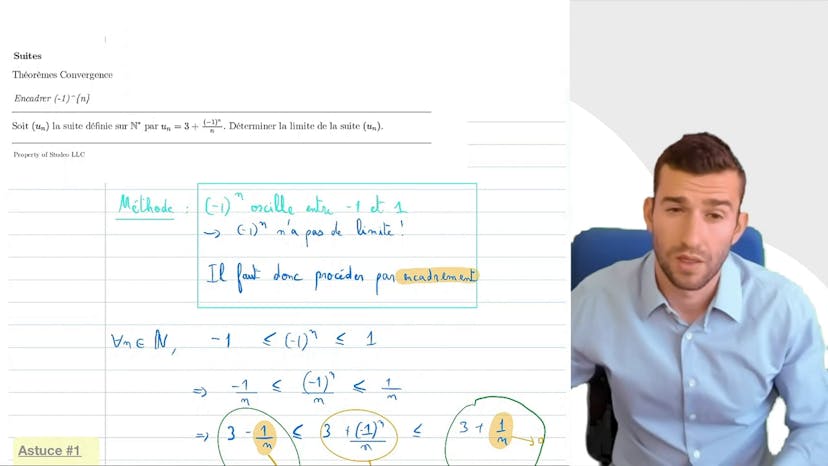
Encadrer (-1)^n

Dans ce cours, on étudie une suite qui contient des termes de la forme "-1 puissance n sur n". Grâce à une analyse asymptotique, on peut voir que cette suite tend vers 3. Pour prouver cela, on utilise la méthode de l'encadrement en multipliant l'expression par un nombre positif, et en ajoutant 3. On arrive à obtenir une expression qui encadre la suite entre 3 moins un sur n et 3 plus un sur n. En utilisant le théorème d'encadrement, on peut prouver que la suite converge vers 3. Cette méthode est très puissante car elle permet non seulement de prouver la convergence, mais aussi de trouver la limite.

Exo TRÈS classique

Dans cette méthode de convergence de suites, on étudie des suites sous forme de fonctions rationnelles, où le degré du numérateur est égal au degré du dénominateur. La limite est le quotient des coefficients dominants de chacun des polynômes. On s'intéresse aux résultats préliminaires comme la majoration, la croissance, et on en déduit la convergence avec les théorèmes de convergence. Pour étudier la monotonie d'une suite, on peut utiliser la méthode du quotient U n+1/U n. On ajoute ensuite les résultats préliminaires pour montrer la convergence. Les exemples présentés montrent comment majorer une suite et déduire la convergence en étudiant la croissance de U n, mais la limite ne sera pas toujours le majorant.

Introduction Trigo

Aucun résumé n'est disponible pour cette vidéo

Dérivabilité de sin et cos

Le cours porte sur les fonctions trigonométriques et leur dérivabilité. Les fonctions sinx et cosx sont dérivables et leur dérivée a une formule simple: sin' x = cosx et cos' x = -sinx. Il est important de se rappeler la courbe de ces fonctions pour éviter de confondre leur dérivée, comme par exemple entre la dérivée de 1/x et celle de la racine carrée de x.Il est conseillé de se souvenir que si une courbe décroit, sa dérivée est négative et si elle croît, sa dérivée est positive. De plus, on peut utiliser les courbes de sinx et cosx pour se rappeler de leur dérivée en sachant que les deux fonctions sont positives au début, sinus est croissante et cosinus est décroissante mais les deux sont positives.En termes de composition, il est important de se rappeler que la formule de la dérivée de la composition s'applique parfaitement pour les fonctions trigonométriques et leur dérivée.

Résolution d'équations

Le cours porte sur la résolution d'équations trigonométriques en utilisant un cercle trigonométrique. Il explique que pour trouver les solutions, il est important de visualiser les angles sur le cercle et de ne pas oublier de considérer les solutions qui pourraient être faciles à voir sur le cercle, mais qui sont souvent négligées. Les solutions pour l'équation cos x sont cos A et sin A, et pour l'équation sin x, ce sont sin A. Les solutions sont soit A ou moins A, soit A ou pi moins A, à deux cas pi près. Le cours illustre également la méthode en utilisant un logiciel de dessin, montrant comment trouver les angles qui partagent le même cosinus ou sinus en traçant des droites verticales ou horizontales sur le cercle trigonométrique. Il explique également la symétrie des angles par rapport aux axes OX et OY, ce qui permet de trouver d'autres solutions en ajoutant 2kpi ou en utilisant des formules spécifiques. Le résumé met l'accent sur l'importance de tracer les droites correctes pour trouver les angles correspondants et donne un aperçu de l'approche visuelle utilisée dans le cours.

Résolution d'inéquations

Cette transcription de la vidéo explique comment résoudre des inéquations simples trigonométriques. Pour cela, il faut déterminer quand cos x est plus petit ou plus grand que cos a, ainsi que le raisonnement symétrique pour sin x et sin a. La méthode consiste à utiliser le cercle trigonométrique et à identifier les points où les abscisses et ordonnées sont plus grandes ou plus petites que d'autres points de référence. Par exemple, pour les points où cos est plus élevé, il s'agit de tous les points sur la partie droite du cercle. Pour les points où cos est plus petit, il s'agit de tous les points sur la partie gauche du cercle. Les résultats peuvent être exprimés en termes d'angles x compris entre a et 2pi moins a. Il est possible d'appliquer le même raisonnement pour le sinus. Il est important de savoir si le professeur colorie les points qui répondent à l'équation ou ceux qu'on veut éviter, pour éviter des erreurs.

Étudier une fonction trigo

Lorsqu'on étudie les fonctions trigonométriques, il est important de prendre en compte certains réflexes. Les étapes classiques pour étudier une fonction visuellement sont: 1. Déterminer le domaine de définition. 2. Vérifier la parité de la fonction. La parité d'une fonction permet de déterminer si la fonction est symétrique par rapport à l'axe OY. Si une fonction est paire, cela signifie que pour tout x, f(-x) = f(x). Si une fonction est impaire, cela signifie qu'elle présente une symétrie par rapport à 0. La parité permet de restreindre l'étude de la fonction à une partie de l'ensemble des réels, ce qui simplifie l'analyse. Ensuite, il est nécessaire de faire une étude des variations en utilisant la dérivée et de représenter la fonction graphiquement. Pour les fonctions trigonométriques, on ajoute une étape supplémentaire: la périodicité. La fonction sinus et cosinus sont des fonctions périodiques, ce qui signifie qu'elles peuvent être réduites à un motif basique qui se répète. Si on trouve que la fonction est périodique, cela permet de réduire encore plus l'étude en se concentrant sur un intervalle, grâce à la période de la fonction. Il faut prendre en compte que la recherche de la périodicité peut ajouter une charge mentale supplémentaire, mais c'est une étape attendue par les professeurs et correcteurs. Un exemple est donné pour illustrer ces concepts de parité et de périodicité, mais l'étude complète n'est pas réalisée dans ce résumé. Il est important d'avoir une structure en tête lorsqu'on résout des exercices, afin de comprendre les questions posées et savoir où elles mènent. Cela permet de se sentir plus en confiance et de mieux maîtriser l'exercice. Ces concepts seront plus développés dans les vidéos de méthode.

Dérivation Composition

Dans cette vidéo, l'enseignant corrige un exercice de dérivation sur des fonctions trigonométriques. Il traite deux questions indépendantes avec les fonctions f qui utilisent des fonctions trigonométriques, en particulier sin et cos. Pour la première question, l'enseignant se rend compte que la fonction f(x) est un quotient, donc il vérifie d'abord l'ensemble de dérivabilité en résolvant l'équation 1+cos(x)=0. Il trouve que cos(x)=-1, ce qui correspond à x=pi+2kpi (avec k appartenant à Z). La fonction est demandée à être étudiée sur l'intervalle ouvert 0pi, donc il n'y a pas de problème d'annulation du dénominateur dans cet intervalle. Appliquant la formule habituelle pour le quotient u/v, qui est u'v-uv'/v^2, il calcule la dérivée en utilisant les dérivées connues de sin et cos. Après avoir développé les termes, il obtient l'expression de la dérivée, f'(x)=(1+cos(x)-sin(x))/(1+cos(x))^2. Pour la deuxième question, il a un produit de deux fonctions trigonométriques, donc il applique la formule du produit (u'v+uv'). Il remarque que les dérivées de cos(2x-1) et sin(5x+3) sont des composées, donc il les calcule en utilisant la règle de dérivation pour les composées. Après avoir substitué les dérivées dans la formule du produit, il obtient f'(x)=-2sin(2x)sin(5x+3)+5cos(2x-1)cos(5x+3). Il remarque que cette expression ressemble à cos(A+B) ou sin(A+B), mais les coefficients -2 et 5 le limitent dans les simplifications possibles. Il conclut en suggérant de pratiquer plus d'exercices similaires pour s'assurer de comprendre les techniques de dérivation, et il recommande de consulter les flashcards pour vérifier les formules de dérivation.

(in)équation trigo

Dans cette vidéo, nous apprenons comment résoudre une équation trigonométrique en utilisant le cercle trigonométrique comme aide visuelle. Nous devons également nous rappeler qu'il peut y avoir deux solutions dans une équation trigonométrique en raison de la périodicité des fonctions trigonométriques. Nous commençons par résoudre l'équation sin(2x + π/4) = √3/2. Nous identifions que √3/2 correspond à sin(π/3) et nous utilisons les valeurs remarquables des fonctions trigonométriques pour trouver les solutions. En utilisant la relation sin A = sin B, nous obtenons deux solutions possibles : 2x + π/4 = π/3 + 2kπ ou 2x + π/4 = π - π/3 + 2kπ. En résolvant ces équations, nous trouvons deux ensembles de solutions : x = π/4 + kπ et x = 5π/24 + kπ. Nous continuons avec une inéquation cos(4x - π/3) < 1,5. Nous identifions que 1,5 correspond à cos(π/3) et nous utilisons le cercle trigonométrique pour trouver les angles ayant un cosinus inférieur à π/3. Nous obtenons une solution comprise entre π/3 et moins π/3 ou 5π/3. Puis, nous résolvons cette équation en utilisant les mêmes étapes que précédemment, et nous trouvons que x doit être compris entre π/6 + kπ/2 et π/2 + kπ/2. Finalement, nous trouvons les valeurs de k pour lesquelles les solutions se trouvent dans l'intervalle 0,2π. Nous trouvons que k doit être compris entre -1/3 et 11/3. En vérifiant que les valeurs de k donnent des solutions qui respectent l'intervalle cherché, nous trouvons les intervalles de solutions suivants : [π/6, π/2] ∪ [2π/3, 7π/6] ∪ [3π/2, 5π/3]. Il est important de poser correctement les équations, de prendre en compte les valeurs de k et de vérifier que toutes les solutions se trouvent dans l'intervalle demandé.

Inéquation de degré 3

Bonjour ! Dans cette vidéo, on va résoudre une inéquation trigonométrique de degré 3. On nous pose une équation trigonométrique avec du cos3x et du cos2x. Pour résoudre ce type d'exercice, on pose généralement grand x égal à cos x ou sin x, selon les cas. En posant ce changement de variable, on obtient une équation en grand x que l'on peut plus facilement résoudre. On vérifie ensuite que f1 égale à 0 pour montrer que 1 est une racine de l'équation. On utilise ensuite cette racine pour factoriser f2x en utilisant la factorisation par la racine. On obtient ainsi une nouvelle équation de degré 2 que l'on peut résoudre en utilisant la méthode habituelle. On détermine ensuite les valeurs de a, b et c pour exprimer f2x sous une forme simplifiée. On étudie ensuite le signe de f en utilisant un tableau de signes. On utilise le changement de variable pour résoudre l'inéquation cos3x-3 cos²x plus 1 super à 0 dans l'intervalle 0,2pi. On retrouve les solutions en utilisant le cercle trigonométrique. On obtient les intervalles de solutions en prenant en compte le fait que grand x doit être compris entre -1 et 1. On résout ainsi l'inéquation de façon rigoureuse. N'oubliez pas d'utiliser le cercle trigonométrique pour bien visualiser les solutions lors de votre raisonnement.