Online Probabilités course by Top Instructors - Probabilités

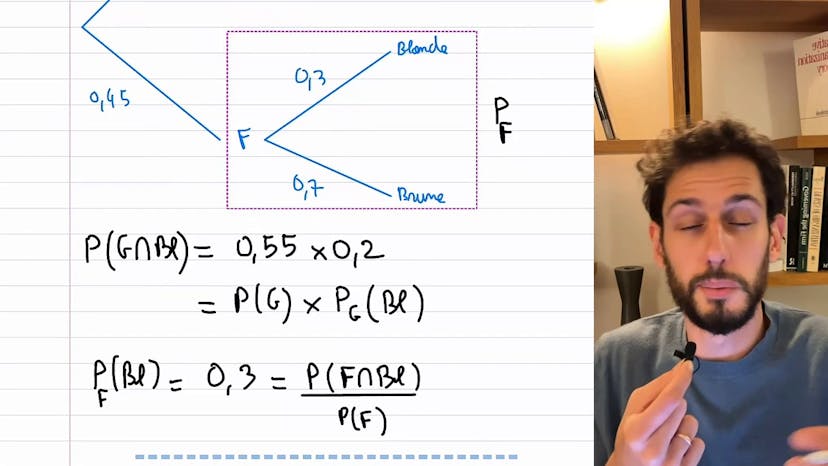
Les probabilités conditionnelles

Lors de l'introduction des probabilités, il est souvent plus facile de commencer par un exemple concret plutôt que des formules théoriques. Dans cet exemple, nous considérerons un lycée où il y a 55% de garçons et 45% de filles. Parmi les garçons, 20% sont blonds et 80% sont bruns. Parmi les filles, 30% sont blondes et 70% sont brunes. Nous pouvons définir les probabilités conditionnelles, qui sont les probabilités dans un sous-univers. Par exemple, la probabilité d'être blond est de 20% pour les garçons et de 30% pour les filles. Chaque probabilité conditionnelle est définie en fonction du sous-univers dans lequel nous nous trouvons. Nous pouvons également calculer la probabilité d'un événement donné en combinant différentes probabilités conditionnelles. Par exemple, la probabilité d'être un garçon blond est de 0,55 (probabilité d'être un garçon) multipliée par 0,2 (probabilité d'être blond parmi les garçons). De même, la probabilité d'être une fille blonde est de 0,45 (probabilité d'être une fille) multipliée par 0,3 (probabilité d'être blond parmi les filles). Nous pouvons aussi exprimer la probabilité d'un événement dans un sous-univers en utilisant la probabilité totale et la probabilité de l'événement dans cet univers. Par exemple, la probabilité d'être blonde parmi les filles est la probabilité d'être une fille blonde divisée par la probabilité d'être une fille. La formule générale pour les probabilités conditionnelles est la probabilité de l'événement B sachant l'événement A, divisée par la probabilité de l'événement A. Cette formule peut être appliquée à n'importe quel événement A et B.

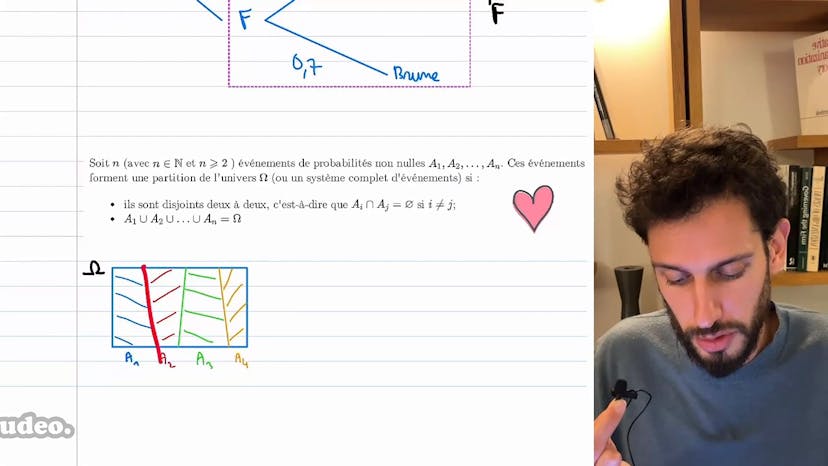
Partition de l'univers

La notion de partition de l'univers est importante en probabilités. Une partition de l'univers consiste à diviser les événements possibles en sous-événements qui n'ont rien en commun. Par exemple, on peut considérer l'univers des garçons comme un sous-univers, et les événements possibles dans ce sous-univers peuvent être les garçons blonds ou les garçons bruns. Une partition est une division de l'univers qui doit satisfaire deux conditions : tous les événements possibles doivent être couverts et il ne doit pas y avoir d'intersection entre les sous-événements. Par exemple, dans l'univers des garçons, on peut diviser en garçons blonds et garçons bruns, mais il ne peut y avoir aucune intersection entre ces deux groupes. On peut également réaliser une partition entre garçons et filles au niveau du lycée. En termes de probabilités, une partition est un ensemble d'événements disjoints qui couvrent tout l'univers. Une partition peut être représentée par des événements a1, a2, ..., an, avec des probabilités associées. Il est important que les événements soient disjoints, c'est-à-dire qu'ils n'aient rien en commun, et que leur union forme tout l'univers.

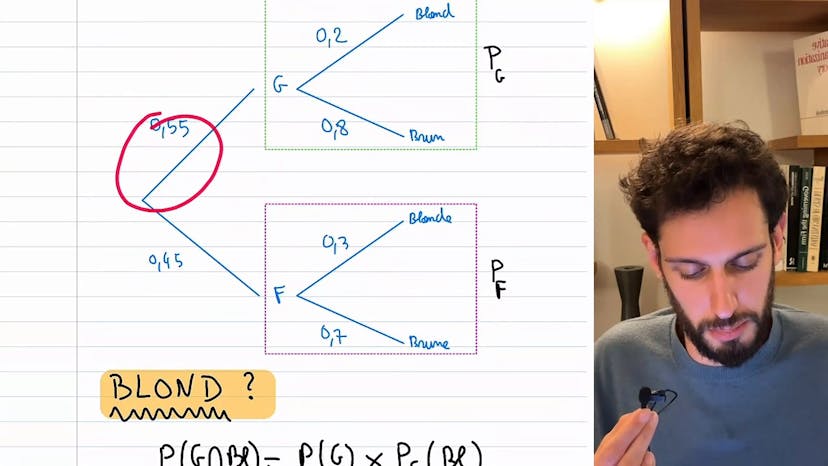
La formule des probas totales

La formule des probabilités totales est une formule très importante que l'on peut appliquer pour calculer des probabilités dans un contexte donné. Dans cet exemple, nous prenons le lycée comme univers et nous créons une partition entre garçons et filles, ainsi qu'entre les différentes couleurs de cheveux. Nous avons utilisé la formule des probabilités conditionnelles pour calculer la probabilité d'être à la fois blond et garçon, en multipliant la probabilité d'être garçon par la probabilité d'être blond parmi les garçons. Maintenant, nous pouvons nous intéresser à une probabilité plus globale, celle d'avoir les cheveux blonds. Imaginons un lycée avec 100 personnes, 55 garçons et 45 filles. Nous voulons savoir quelle est la probabilité, en tirant une personne au hasard, de tomber sur quelqu'un qui a les cheveux blonds, qu'il soit garçon ou fille. L'idée est de ne pas se focaliser uniquement sur les personnes blondes, mais de prendre en compte les deux catégories. Il y a deux chemins possibles pour tirer une personne blonde : soit on tire un garçon blond, soit on tire une fille blonde. La formule des probabilités totales consiste à sommer les probabilités de ces deux événements pour obtenir la probabilité d'être blond. En d'autres termes, la probabilité d'être blond est égale à la probabilité d'être un garçon blond plus la probabilité d'être une fille blonde. On peut aussi écrire cela en utilisant la formule des probabilités conditionnelles. Cette formule nous permet de parcourir toutes les branches de l'arbre des événements et de les sommer pour obtenir la probabilité recherchée. En théorie, si nous avons une partition de l'univers, la probabilité d'un événement B est égale à la somme des probabilités de B dans chaque branche de la partition. Cette formule peut être utilisée en remplaçant chaque probabilité par la formule des probabilités conditionnelles correspondante. Il est important de comprendre intuitivement le sens de cette formule : nous cherchons l'événement dans chaque branche et les sommons toutes. J'espère que cela était clair. N'hésitez pas à laisser des commentaires si nécessaire. À bientôt dans une prochaine vidéo !

Indépendance

L'indépendance, une notion très importante en probabilité, peut être expliquée de manière claire en utilisant des exemples. Dans cet exemple, nous avons deux variables : le sexe (garçon ou fille) et la couleur des cheveux (blond ou brun). Nous avons également des probabilités associées à chaque événement. Par exemple, la probabilité d'être blond en étant garçon est de 0,2, et la probabilité d'être blond en étant fille est de 0,3. Pour déterminer la probabilité d'être blond dans ce lycée, nous utilisons la formule des probabilités totales. Cependant, il est important de noter que la couleur des cheveux dépend du sexe. Par conséquent, la probabilité d'être blond dépend de si vous êtes un garçon ou une fille. Ces événements sont donc dépendants. Cependant, il est également possible d'avoir des événements indépendants. Par exemple, si la probabilité d'être blond est la même pour les garçons et les filles, il s'agit d'un événement indépendant. Dans ce cas, peu importe si vous êtes un garçon ou une fille, la probabilité d'être blond est de 30%. Il est important de comprendre les définitions formelles en mathématiques, mais il est également utile de les considérer avec des exemples concrets. Les formalités théoriques viennent ensuite pour renforcer la compréhension. Il est également intéressant de noter que si deux événements A et B sont indépendants, leurs complémentaires (non A et non B) le sont également. En résumé, l'indépendance en probabilité se réfère à des événements qui ne dépendent pas les uns des autres. Dans le cas de l'exemple, si la probabilité d'être blond ne dépend pas du sexe, alors ces événements sont indépendants.

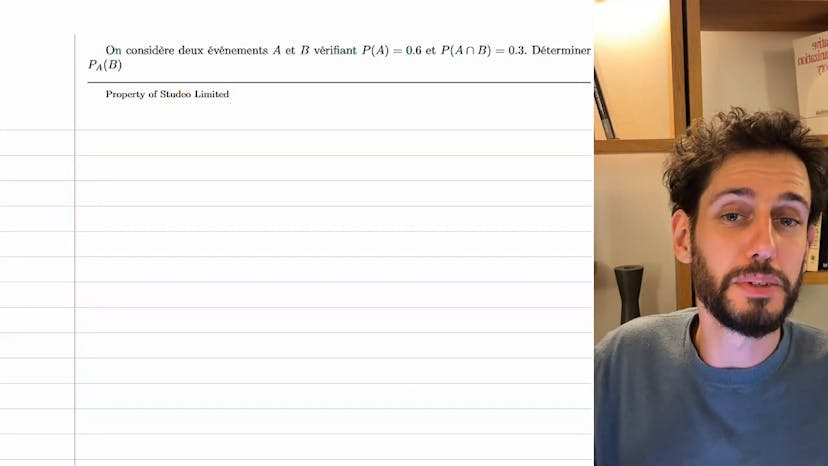
Application calculatoire

Dans ce cours, nous allons apprendre à appliquer la formule des probabilités conditionnelles. Tout d'abord, nous avons deux événements, A et B. Nous voulons trouver P2B sachant A, en utilisant la formule des probabilités conditionnelles. Cette formule est P2A inter B divisé par P2A. Nous trouvons donc que P2B sachant A est égal à 0,3 sur 0,6, ce qui est égal à 1,5. Pour mieux comprendre, il est possible de représenter ces événements dans un arbre qui montre les différentes possibilités. En résumé, ceci est une application basique de la formule des probabilités conditionnelles. N'hésitez pas à poser des questions si nécessaire. Maintenant, passons à la prochaine vidéo.

Application avec contexte

La probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de la marque A peut être calculée en utilisant la formule des probabilités conditionnelles. Pour commencer, on sait que 60% des voitures fabriquées sont des voitures hybrides. Donc la probabilité d'avoir une voiture hybride est de 0,6, tandis que la probabilité de ne pas avoir une voiture hybride est de 0,4. Ensuite, parmi les voitures hybrides, 70% d'entre elles sont de la marque A. Donc la probabilité d'avoir une voiture hybride de la marque A est de 0,6 * 0,7 = 0,42. En utilisant ces informations, nous pouvons en conclure que la probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de la marque A est de 0,42. Cette méthode utilise un arbre pour représenter les différents événements et permet de calculer la probabilité conditionnelle en utilisant la formule adéquate.

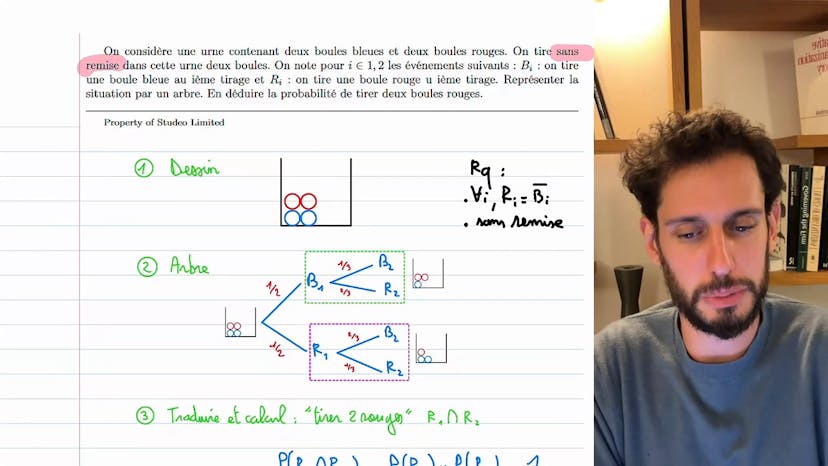
Arbre et urne sans remise

Dans ce cours, nous étudions une situation où nous tirons des boules d'une urne sans les remettre. Il est important de faire la distinction entre une situation avec remise (où l'on remet la boule après chaque tirage) et sans remise (où la boule tirée est retirée de l'urne). Cette distinction va influencer les probabilités tout au long du problème. Nous utilisons les notations "bi" pour représenter le fait de tirer une boule bleue au ième tirage et "ri" pour représenter le fait de tirer une boule rouge. Vu qu'il n'y a que des boules bleues et rouges dans l'urne, nous pouvons remarquer que "ri" est équivalent à "bi barre" (le complémentaire de "bi"). Par exemple, si "b1" représente le fait de tirer une boule bleue au premier tirage, alors "r1" représente le fait de ne pas tirer une boule bleue au premier tirage (c'est-à-dire tirer une boule rouge). L'idée ici est de représenter la situation par un arbre. Cela nous permet de visualiser plus clairement les différentes probabilités. En utilisant des dessins, nous pouvons rendre la situation plus compréhensible. Au fur et à mesure des tirages, nous modifions notre arbre pour refléter les probabilités en cours. Par exemple, si nous avons tiré une boule bleue au premier tirage, nous aurons alors une chance sur deux d'en tirer une deuxième, puis une chance sur trois d'en tirer une troisième. Pour traduire cela en calculs, nous pouvons utiliser les probabilités conditionnelles. Par exemple, pour calculer la probabilité d'avoir tiré deux boules rouges, nous pouvons écrire "proba de R1 inter R2". Cette expression équivaut à la probabilité d'avoir tiré une boule rouge au premier tirage, puis dans cet univers, la probabilité d'avoir tiré une boule rouge au deuxième tirage. En résolvant ces calculs, nous obtenons les probabilités recherchées. Dans cet exemple, la probabilité d'avoir tiré deux boules rouges est de 1/6. Il est important de bien comprendre les énoncés et de faire attention à la présence ou non de remise dans le problème. N'hésitez pas à poser des questions si quelque chose n'est pas clair et je vous retrouve dans une prochaine vidéo.

Indépendance : calculatoire

Dans cet exercice, nous avons une entreprise qui a deux rendez-vous avec deux fournisseurs différents. Nous allons essayer de faire signer un contrat au premier fournisseur avec une probabilité de 0,7 et au deuxième fournisseur avec une probabilité de 0,4. Les deux événements sont considérés comme indépendants, ce qui signifie que la signature d'un contrat avec le premier fournisseur n'exclut pas la possibilité de signer également un contrat avec le deuxième fournisseur. Maintenant, nous devons calculer la probabilité de deux événements. Tout d'abord, nous définissons les événements comme suit : S1 représente la signature d'un contrat avec le fournisseur 1, S2 représente la signature d'un contrat avec le fournisseur 2. L'événement "aucun contrat" signifie qu'aucun contrat n'est signé, ni avec le fournisseur 1 ni avec le fournisseur 2. Donc, cela correspond à S1 bar (non signé avec le fournisseur 1) intersecté avec S2 bar (non signé avec le fournisseur 2). L'événement "au moins un contrat" est le complémentaire de l'événement "aucun contrat". Donc, nous pouvons utiliser la probabilité de l'événement "aucun contrat" pour calculer la probabilité de "au moins un contrat", en utilisant la formule : P(au moins un contrat) = 1 - P(aucun contrat). En utilisant la propriété d'indépendance des événements S1 et S2, nous savons que P(S1 bar intersect S2 bar) est équivalent à P(S1 bar) * P(S2 bar). Donc, nous pouvons calculer la probabilité de "aucun contrat" en remplaçant chaque probabilité par 1 moins la probabilité de l'événement de base. Ainsi, nous avons 0,3 * 0,6 = 0,18 pour la probabilité de "aucun contrat". Par conséquent, la probabilité de "au moins un contrat" est égale à 1 - 0,18 = 0,82, soit 82%. En résumé, il y a 82% de chances que l'entreprise signe au moins un contrat avec l'un des deux fournisseurs. Cela inclut également la possibilité de signer des contrats avec les deux fournisseurs. Il est important de clarifier les événements et de tenir compte de l'indépendance entre eux lors de la résolution du problème.

Indépendance : définition

Dans cet exercice, on nous donne des informations sur la population française: 90% des personnes sont droitières et 45% sont myopes. On nous dit également que parmi les myopes, 10% ne sont pas droitières. On nous demande si les événements "être droitière" et "être myope" sont indépendants. Pour répondre à cette question, nous devons analyser les probabilités. Premièrement, nous traduisons l'énoncé en termes de probabilités. Être droitière a une probabilité de 90% pour un français, tandis que être myope a une probabilité de 45%. De plus, parmi les myopes, il y a une probabilité de 10% de ne pas être droitière. En regardant ces informations, nous remarquons que la probabilité de ne pas être droitière parmi les myopes est de 0,1. Cela implique que la probabilité d'être droitière parmi les myopes est de 0,9 (puisque la somme des probabilités doit être égale à 1). Maintenant, nous pouvons répondre à la question de savoir si les événements sont indépendants. Si être droitière est indépendant d'être myope, cela signifie que connaître si quelqu'un est myope ou pas ne change pas la probabilité d'être droitière. Dans notre cas, la probabilité d'être droitière est de 0,9, que l'on soit myope ou pas. Donc, d'après cette analyse, nous pouvons conclure que la myopie et le fait d'être droitière sont indépendants.

Écriture ensembliste

Dans cet exercice, on nous donne trois événements, A, B et C, de l'univers Omega. Le but est de traduire ces phrases en termes d'ensembles. En utilisant les symboles d'union, d'intersection et le complémentaire, on peut représenter ces phrases de la manière suivante : - Seul A se réalise : A ∩ B' ∩ C' - A et B se réalisent, mais pas C : A ∩ B ∩ C' - Les trois événements se réalisent : A ∩ B ∩ C - Au moins l'un des trois événements se réalise : A ∪ B ∪ C - Au moins deux des trois événements se réalisent : (A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C) - Aucun ne se réalise : A' ∩ B' ∩ C' - Au plus l'un des trois se réalise : Ω - (A ∪ B ∪ C) - Exactement deux des trois se réalisent : (A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C) - (A ∩ B ∩ C) Voilà pour le résumé en termes SEO-friendly de cet exercice.

Probabilité de l’intersection

Dans cet exercice, nous voulons illustrer une inégalité concernant la probabilité de l'intersection de deux événements. Plus précisément, nous voulons montrer que cette probabilité est comprise entre deux valeurs. Pour commencer, nous allons examiner la partie de droite de l'inégalité. La probabilité de l'intersection est égale à la plus petite valeur entre 0 et la somme des probabilités des deux événements moins 1, ainsi que le minimum des probabilités individuelles. Pour le démontrer, nous utilisons la formule appropriée. Une autre méthode aurait pu être utilisée, mais j'ai préféré utiliser cette approche. Nous utilisons la formule et constatons que l'événement A est inclus dans l'union, tout comme B. Par conséquent, la probabilité de l'union est plus grande que celle de A et aussi que celle de B. En conséquence, P(A∩B) est négatif par rapport à P(A) et P(B). De même, P(B∩A) est également négatif par rapport à P(B) et P(A∪B). En remplaçant ces valeurs dans l'inégalité, nous constatons que P(A∩B) est plus petit à la fois que P(A) et que P(B), ce qui signifie qu'il est plus petit que le minimum des deux probabilités. Ensuite, nous montrons l'égalité dans l'autre sens. Tout d'abord, nous devons démontrer que la probabilité de l'intersection est plus grande que le maximum des deux probabilités. Cela signifie que nous devons montrer qu'elle est plus grande que l'une et plus grande que l'autre. Nous savons que cela est supérieur à zéro car il s'agit d'une probabilité. Il nous reste à prouver qu'elle est plus grande que la valeur maximale. Comme je l'ai mentionné précédemment, P(A∪B) est plus petit que 1, donc P(A∩B), qui est égal à P(A) + P(B) - P(A∪B), est plus grand que P(A)+P(B)-1. Par conséquent, il est plus grand que zéro et que cette valeur maximale, ce qui conclut notre exercice.

Inégalité de Bonferroni

Dans cet exercice, nous souhaitons démontrer la formule de la probabilité de l'intersection de n événements, qui est supérieure ou égale à la somme des probabilités moins n moins 1. Nous allons le démontrer par récurrence pour n supérieur ou égal à 2. L'initialisation se fait pour n=2. Dans ce cas, la probabilité de l'intersection est égale à la somme des probabilités moins 1. En utilisant la formule P(A)+P(B)-P(A∪B), nous obtenons bien P(A1)+P(A2)-1. Ensuite, nous passons à l'hérédité. La probabilité de l'intersection allant jusqu'à n+1 est égale à la probabilité de l'intersection allant jusqu'à n, multipliée par la probabilité n+1, moins la probabilité de cette intersection union An+1. Nous avons utilisé la formule P(A)+P(B)-P(A∪B), où A représente l'intersection allant jusqu'à n et B représente l'événement n+1. En utilisant l'hypothèse de récurrence, qui nous dit que cette probabilité est supérieure ou égale à la somme des Pi moins n moins 1, nous pouvons réinjecter P(An+1) dans la somme et obtenir moins n plus 1, correspondant à n+1 moins 1 dans la formule. Ainsi, nous avons démontré l'hérédité, et donc la récurrence était assez rapide à faire. Nous obtenons donc la formule demandée pour la probabilité de l'intersection de n événements.

Loi de dés pipés

Dans cet exercice, il s'agit de modéliser une expérience aléatoire avec un dé pipé, où la probabilité d'obtenir une face est proportionnelle au chiffre sur cette face. La probabilité de faire 1 est notée x, donc la probabilité de faire 2 est de 2x, et ainsi de suite jusqu'à 6x, pour que cela soit proportionnel. La somme de toutes ces probabilités doit égaler 1. On obtient donc l'équation x + 2x + 3x + 4x + 5x + 6x = 1, ce qui donne 21x = 1. Donc x = 1/21, qui est notre probabilité pour faire 1. Ensuite, on cherche la probabilité d'obtenir un chiffre pair, en faisant la somme des probabilités des événements correspondants (2, 4 et 6). Les événements sont mutuellement exclusifs, donc on peut simplement additionner les probabilités. Donc on a 2/21 + 4/21 + 6/21 = 12/21, simplifié en 4/7. Dans la seconde partie de l'exercice, on refait la même chose, mais cette fois-ci avec une nouvelle distribution de probabilités. On veut que la probabilité d'obtenir une face paire soit le double de celle d'obtenir une face impaire. Donc on a x pour une face impaire, et 2x pour une face paire. La somme de toutes ces probabilités doit encore égaler 1. On a donc l'équation x + 2x + x + 2x + x + 2x = 1, soit 9x = 1. Donc x = 1/9, notre probabilité pour une face impaire. Ensuite, on cherche la probabilité d'obtenir une face paire, en additionnant les probabilités correspondantes (2x pour chaque face paire). Donc on a 2/9 + 2/9 + 2/9 = 2/3. C'est tout pour cet exercice.