 All subjects
All subjects
 All subjects
All subjects
Maths Expertes
Complexes
Terminale
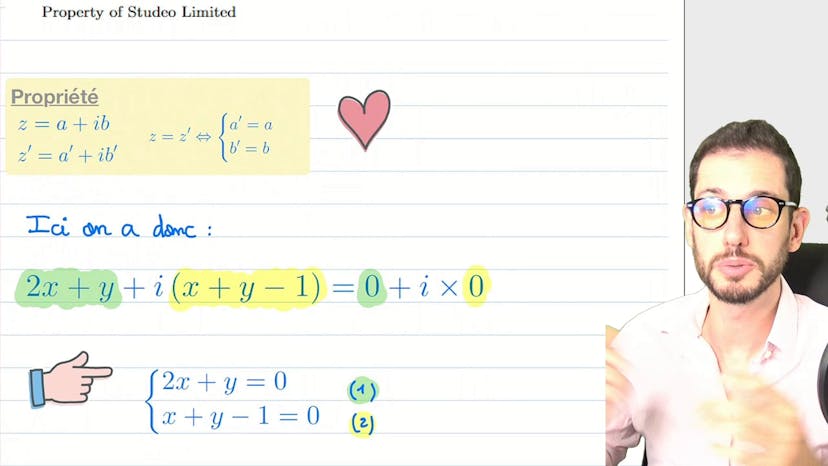
Partie réelle et imaginaire
Ce cours explique les bases des nombres complexes, qui sont des nombres ayant une partie réelle et une partie imaginaire. Lorsqu'on a une équation de complexe, on peut identifier deux complexes en utilisant la partie réelle et la partie imaginaire, ce qui donne deux équations. On peut alors résoudre le système pour trouver les solutions. L'astuce est de mettre tout à gauche égal à 0 pour obtenir les deux équations.
Maths Expertes
Complexes
Terminale

Rappel : le conjugué
Le cours parle du conjugué d'un nombre complexe, qui est défini comme la quantité a moins ib. Il explique que le conjugué a des propriétés simples, telles que la conjuguaison de la somme étant la somme des conjugués et la conjuguaison du produit étant le produit des conjugués. Ensuite, le cours montre comment résoudre une équation complexe en introduisant des variables a et b pour séparer les parties réelles et imaginaires, en utilisant la méthode basique. Le cours recommande l'utilisation de cette méthode pour résoudre ce type d'équations, en l'absence d'astuces plus avancées. Le cours se termine en invitant les étudiants à poser des questions et en leur disant au revoir.
Maths Expertes
Complexes
Terminale
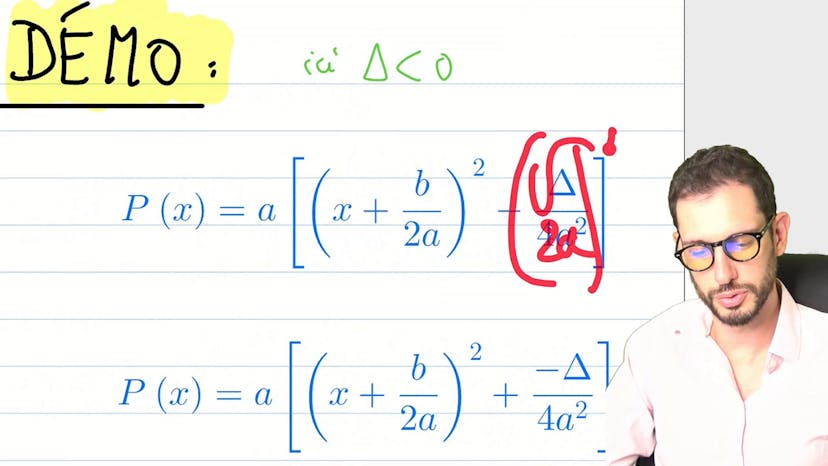
Second degré Δ<0
Ce cours traite des racines d'un polynôme de second degré. En mathématiques, lorsqu'on avait un polynôme ax²+bx+c, on pouvait utiliser le delta pour trouver les solutions, qui étaient soit deux valeurs réelles, une valeur réelle, ou deux valeurs imaginaires conjuguées. Cependant, si on inclut l'utilisation des nombres complexes, on peut trouver des racines imaginaires conjuguées même lorsque delta est négatif. Une démonstration rapide est présentée pour expliquer ce phénomène, suivie d'un exemple pour illustrer le concept. Mots-clés SEO: polynôme de second degré, delta, racines, nombres réels, nombres complexes.
Maths Expertes
Complexes
Terminale

Quantité conjuguée
Ce cours explique une méthode classique pour trouver la forme algébrique de certains nombres complexes. Il rappelle la notion de quantité conjuguée que l'on utilise pour multiplier en haut et en bas par un nombre bien choisi afin de se débarrasser des racines au dénominateur. Cette méthode s'applique également aux nombres complexes. L'exemple d'équation est présenté et expliqué pas-à-pas pour montrer comment trouver la forme algébrique. Il est important de bien connaître cette méthode pour pouvoir exprimer les nombres complexes sous forme algébrique.
Maths Expertes
Complexes
Terminale

Z est-il réel ? V1
Le cours présente une méthode classique pour résoudre un exercice de complexe. L'exercice consiste à trouver l'ensemble des z tels que grand z, petit z moins 1 divisé par petit z plus 1 soit réelle. La méthode consiste à poser a et b appartenant à R, et à utiliser la propriété selon laquelle z quelconque est un réel si et seulement si la partie imaginaire de z est nulle. Les calculs sont effectués en posant petit z égal à a plus ib et en utilisant la quantité conjuguée pour simplifier l'expression. Finalement, on trouve que z est réel uniquement si b est nul, ce qui donne l'ensemble des z réels moins l'élément moins 1.
Maths Expertes
Complexes
Terminale

Z est-il réel ? V2
Dans ce cours de mathématiques, on apprend la méthode pour déterminer si un nombre complexe est réel. Un nombre complexe est égal à son conjugué si sa partie imaginaire est opposée et sa partie réelle est la même. On peut appliquer les propriétés de la conjugaison pour simplifier l'équation. En utilisant ces propriétés, on peut arriver à la conclusion que si z est égal à son conjugué, alors z est réel. Cette méthode est élégante mais pas toujours optimale. Il faut connaître les notions de conjugué et le chapitre sur les nombres complexes pour bien comprendre cette méthode.
Maths Expertes
Complexes
Terminale
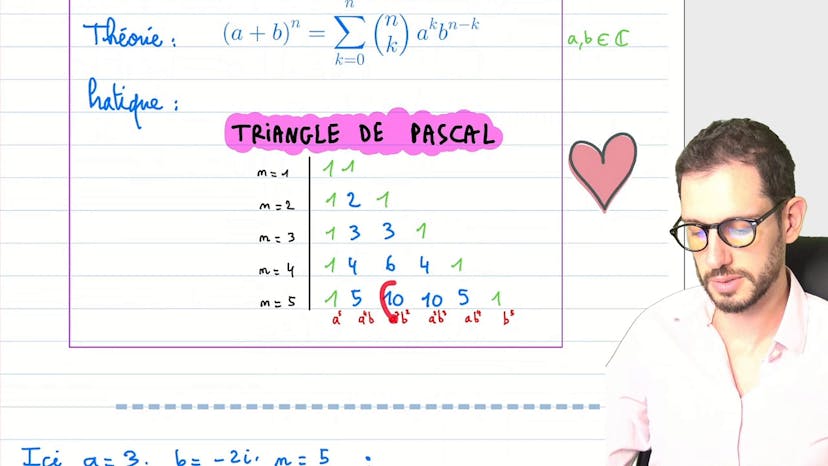
Binôme de Newton
Le cours se concentre sur la formule du binôme de Newton, qui donne la valeur de (A + B)^n pour tout complexe A et B. Le cours explique que la formule est valable pour n'importe quel nombre positif n. La formule est assez compliquée, mais elle peut être simplifiée en utilisant le triangle de Pascal. Pour utiliser le triangle de Pascal, on commence par trouver le coefficient 1 et on utilise ensuite une formule pour trouver les coefficients suivants. Le cours donne un exemple pour la valeur de (3-2i)^5 en utilisant cette méthode.
Maths Expertes
Complexes
Terminale

Equation bicarré complexe
Ce cours porte sur la résolution d'une équation bicarrée qui est une équation de degré 4 sans terme en x3 ni terme en x. On utilise un changement de variable pour se ramener à un polynôme du degré 2, que l'on peut résoudre, en complexe ou en réel. La méthode consiste à poser Z égale z2 et à résoudre pour grand Z en utilisant les racines évidentes et le produit des racines. Ensuite, on résout pour petit z en se rappelant que grand Z est égal à grand z1 ou grand z2 et en gérant la partie complexe si grand z2 est négatif. Les solutions de l'équation bicarrée sont ensuite données en fonction de racines carrées et d'imaginaires. Le fait de ne pas avoir de termes en x3 ni en x permet de se rapporter à un polynôme du degré 2 et de procéder de manière assez logique pour trouver les solutions.
Maths Expertes
Complexes
Terminale

Factoriser un cube ?!
Dans cette leçon sur les complexes, il est demandé de factoriser une expression. Avant de se lancer dans la factorisation, il est recommandé d'observer les puissances successives de i pour identifier une astuce. En remarquant que 27 = 3^3 et que 8 = 2^3, et en connaissant la formule pour la somme de deux cubes, on peut exprimer 27z³-8i comme étant égal à 3z le tout au cube plus 2i le tout au cube. En appliquant la formule pour la somme de deux cubes, on peut factoriser l'expression. Cette méthode est avancée, mais elle permet de gagner du temps dans la résolution d'exercices.
Maths Expertes
Complexes
Terminale
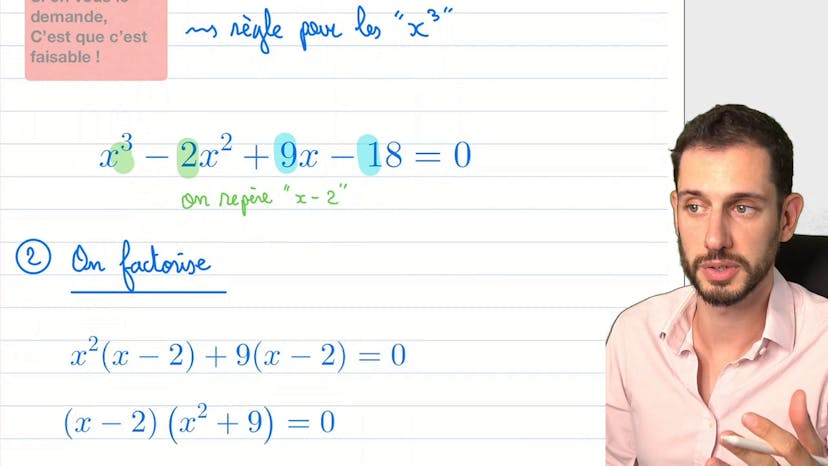
Factoriser un cube pire !!
Dans cette transcription vidéo, le professeur rappelle l'importance de bien connaître son cours pour résoudre des exercices difficiles. Pour ne pas paniquer, il conseille d'observer attentivement les éléments de l'exercice pour en trouver une astuce. Ainsi, en repérant un x-2 et des chiffres comme 9 et 18, il propose de factoriser par 9 et de trouver un facteur commun pour x² et x-2. Grâce à cette astuce, la factorisation est trouvée et il est facile ensuite de résoudre pour trouver les trois solutions: 2, 3i et -3i. Le professeur encourage les élèves à poser des questions et leur donne rendez-vous dans une prochaine vidéo.


