 All subjects
All subjects
 All subjects
All subjects
Maths Spé
Analyse
Terminale

Introduction Limites
Dans ce cours, on parle de limites de fonctions. Comparé aux limites de suites, qui portent uniquement sur les entiers, les fonctions se portent sur l'ensemble des réels, ce qui rend la tâche plus complexe. On peut parler de limites en l'infini (lorsque X tend vers l'infini), en un réel (lorsque X tend vers un réel spécifique), ou même de limite inexistante (lorsqu'il y a une oscillation infinie). On peut approcher les limites en analysant des graphes, comme celui d'une fonction qui se colle à une valeur réelle, qui tend vers l'infini, ou qui oscille très haut avant/derrière une valeur réelle. Les méthodes d'analyse comprennent une analyse graphique, le calcul de limites et la détermination d'asymptotes horizontales ou obliques. Il est important de comprendre les définitions et de savoir reconnaître les différents types de limites de fonctions.
Maths Spé
Analyse
Terminale

En l'infini, limites finies et infinies
Le cours traite de la notion de limite d'une fonction lorsque la variable x tend vers plus l'infini. Il y a deux définitions à connaître : lorsque la fonction tend vers plus l'infini et lorsque la fonction tend vers un réel L. Pour une fonction qui tend vers plus l'infini, cela signifie que pour tout plateau Y égal à un grand A choisi arbitrairement, la fonction finit toujours par dépasser complètement ce plateau. Pour une fonction qui tend vers un réel L, cela signifie que toutes les valeurs de la fonction finissent toujours par être dans un couloir, quelle que soit la largeur du couloir autour de la limite. Les définitions formelles sont ensuite données, avec des exemples graphiques pour illustrer la notion de couloir. Les définitions peuvent être utilisées pour résoudre des exercices, et il est important de les comprendre pour obtenir de bons résultats dans ce domaine.
Maths Spé
Analyse
Terminale

Les asymptotes horizontales
Découvrez dans cette vidéo les limites de fonction lorsque x converge vers l'infini et ce qu'est une asymptote. Il y aura plusieurs types d'asymptote, mais ici nous allons nous concentrer principalement sur une asymptote horizontale, qui est en fait une droite vers laquelle la courbe de f va venir se coller.Lorsque la limite de f, lorsque x tend vers l'infini, converge vers un réel, que l'on appelle L, la courbe se colle à une droite. Il est important de noter qu'il ne s'agit pas de l'asymptote de la fonction f, mais de celle de sa courbe.Il est possible de se coller à une droite de différentes manières, à la fois croissante et décroissante. Il est également possible d'avoir une asymptote horizontale avec une fonction sinus.En résumé, une asymptote horizontale est une droite vers laquelle la courbe de F se rapproche infiniment proche. C'est une notion liée à la vision assez intuitive qu'on peut avoir de la limite.
Maths Spé
Analyse
Terminale
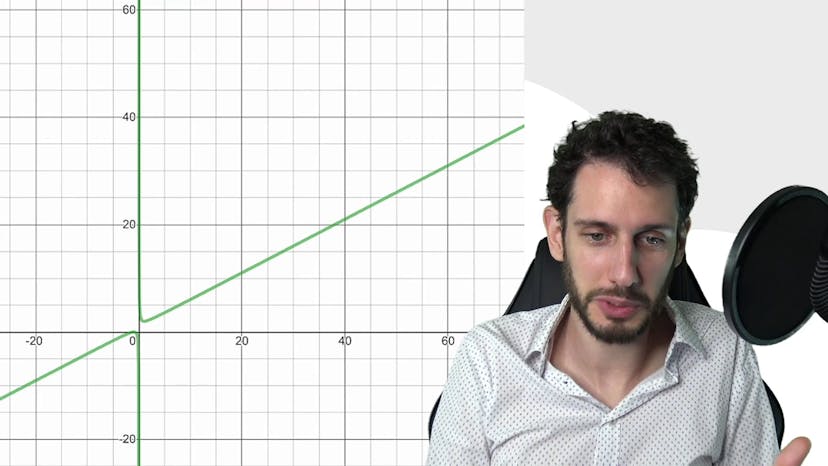
Bonus : Les asymptotes obliques
Dans cette vidéo, on parle de l'asymptote oblique, qui est une droite inclinée qui se rapproche de la courbe d'une fonction dans la direction de plus infini ou moins infini. Lorsque la différence entre la valeur de la fonction et la droite tend vers 0, on dit que la droite est une asymptote oblique à la courbe. Ce concept est important en mathématiques et est souvent utilisé dans les exercices. Une illustration simple est donnée pour montrer comment une courbe tend vers une droite affine en plus infini ou moins infini. L'asymptote horizontale est également une autre question importante qui sera traitée dans une autre vidéo.
Maths Spé
Analyse
Terminale

En un point réel, limite infinie
Le cours aborde les limites de fonction avec x tendant vers un réel a. On distingue deux cas principaux : lorsque f tend vers plus ou moins l'infini et lorsque f converge vers une valeur finie. Les limites sont définies selon la capacité de la fonction à dépasser un plateau donné. La notion de limite à gauche et limite à droite est abordée. La définition de l'asymptote verticale est présentée pour les cas où la limite infinie est atteinte en un point fini.
Maths Spé
Analyse
Terminale
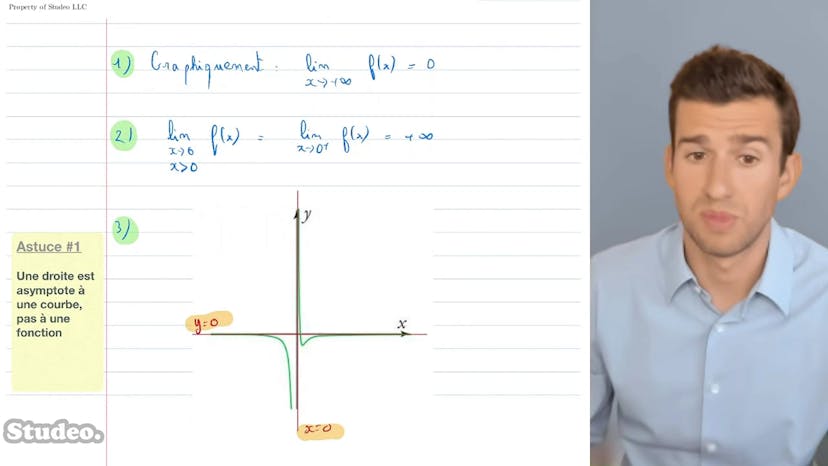
Analyse graphique
Dans ce cours, nous examinons les limites de fonctions en utilisant une analyse graphique. Nous examinons une fonction tracée et déterminons ses limites en examinant son comportement lorsque x tend vers plus ou moins l'infini. En utilisant cette méthode, nous pouvons identifier les asymptotes verticales et horizontales de la courbe. Les équations des asymptotes sont de la forme y = a pour une droite horizontale et x = a pour une droite verticale. Nous faisons également deux remarques: premièrement, une droite est l'asymptote à une courbe, pas à une fonction. Deuxièmement, une droite peut être l'asymptote en deux endroits.
Maths Spé
Analyse
Terminale

Calcul limite en un point fini par factorisation
Dans ce cours, nous apprenons comment trouver une limite en 1 pour une fonction avec une forme indéterminée. Pour cela, nous pouvons factoriser la fonction pour lever l'indétermination. Le premier exemple est facile à factoriser à l'aide de l'identité remarquable, ce qui nous donne une limite de 0. Le deuxième exemple nécessite la factorisation d'un polynôme à l'aide de la méthode classique pour trouver les racines. Nous trouvons ainsi 2 racines, que nous pouvons utiliser pour factoriser la fonction et trouver une limite de 1/2. Nous notons que la fonction tend vers 0 à gauche et à droite de 1, et précisons ses limites en 1+, 1- et leur influence sur le quotient avec une autre fonction. Cette méthode est utile lorsque nous pouvons factoriser la fonction pour simplifier le calcul des limites.
Maths Spé
Analyse
Terminale

Determiner une asymptote + étude
Pour trouver les asymptotes d'une fonction, il faut regarder en plus l'infini, en moins l'infini et les bords de l'ensemble de définition de la fonction. Par exemple, pour la fonction f(x) = -2/(1-x) définie sur R privé de 1, il faut regarder en moins et plus l'infini, ainsi qu'en 1. En moins et plus l'infini, on a une asymptote horizontale d'équation y = 0. En 1, il y a une asymptote verticale d'équation x=1. Pour déterminer si on tend vers plus ou moins à un point donné, il faut prendre des valeurs autour pour être sûr.
Maths Spé
Analyse
Terminale
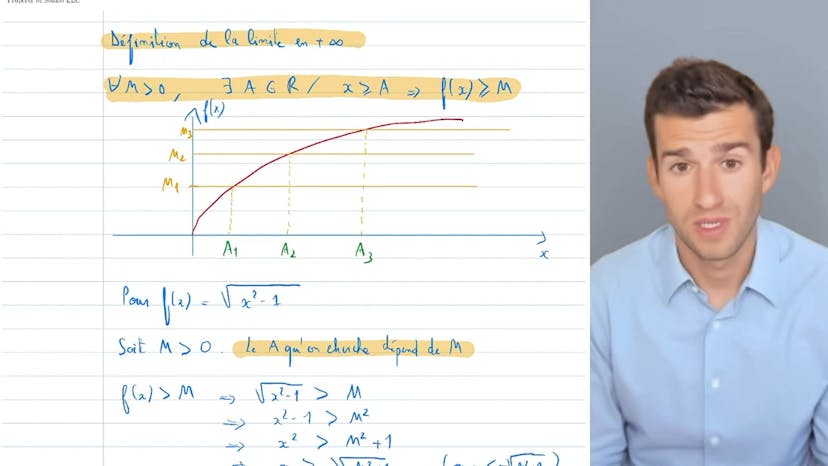
Calcul de limite infinie avec la définition (trouver un A)
Dans ce cours, nous avons abordé la définition formelle de la limite, qui peut sembler difficile à comprendre pour certains élèves. Nous avons expliqué que la limite est atteinte lorsque la fonction tend vers une valeur infinie, ce qui signifie qu'à un certain moment, la fonction dépassera toujours un certain point. Nous avons utilisé l'exemple d'une fonction racine carrée pour illustrer cette idée. Ensuite, nous avons examiné une autre fonction, racine de x au carré moins un, et avons expliqué comment trouver la valeur de a qui convient à un certain point m. Cela implique de résoudre une inéquation. Nous avons montré comment cette approche peut être utilisée pour démontrer que la fonction tend vers l'infini lorsque x tend vers l'infini.En somme, la résolution d'équations est la méthode clé utilisée pour résoudre les problèmes concrets et pour pratiquer la définition formelle de la limite.
Maths Spé
Analyse
Terminale
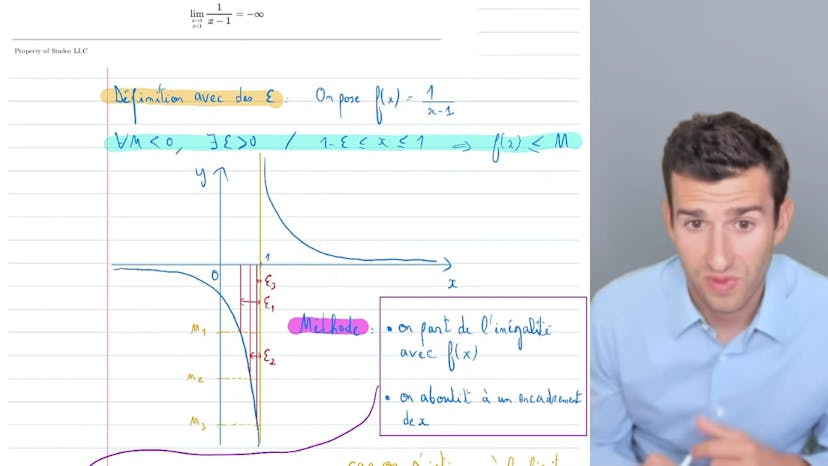
Calcul de limite finie avec la définition (trouver un epsilon)
Dans ce cours, on apprend à calculer la limite infinie en utilisant la définition avec les epsilon. Le but est de montrer que la fonction tend vers moins l'infini en un réel fixé. Pour cela, on prend un réel négatif m et on cherche à résoudre f2x inférieur à m. On trouve alors un encadrement de x qui permet de déterminer un intervalle où la fonction est inférieure à m. On utilise l'inverse de la fonction pour vérifier que l'on est sur le bon intervalle. Le but est de trouver le y qui convient en déroulant les calculs petit à petit. L'exercice demande de la pratique, mais avec de l'exercice, on peut y arriver.
Maths Spé
Analyse
Terminale
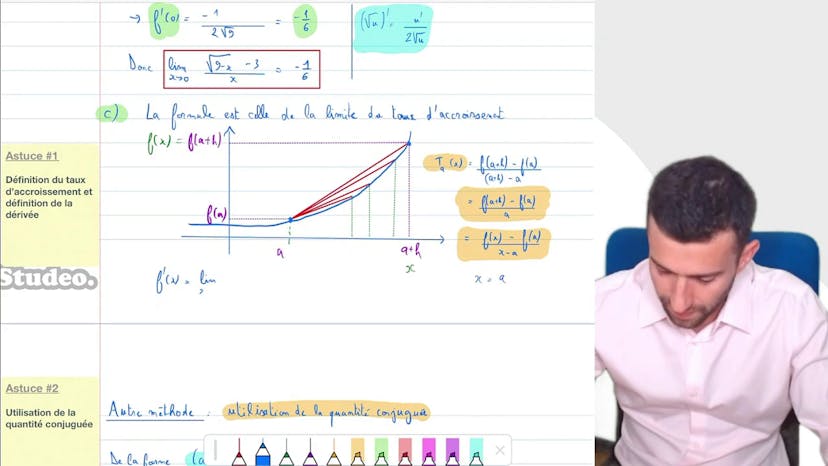
Utilisation de la dérivée
Dans ce cours, nous corrigeons un exercice sur les limites utilisant le taux d'accroissement et la dérivée. L'objectif est de se familiariser avec les limites qui sont un peu plus compliquées en utilisant la dérivée.
La première question demande d'utiliser la dérivée pour trouver la limite de la fonction f(x) = √(9 - x) quand x tend vers 0. Pour cela, nous utilisons la définition du taux d'accroissement et nous réécrivons la formule de la limite en utilisant la dérivée. En utilisant la définition de la dérivée, nous trouvons que la dérivée de f(x) est -1/(6√(9 - x)). Nous calculons ensuite la dérivée en x = 0 et trouvons que f'(0) = -1/6. Ainsi, la limite de √(9x) - 3/x quand x tend vers 0 est -1/6.
La deuxième question nous demande de trouver la limite de la fonction f(x) = √(2x - 1)/x en utilisant le même raisonnement. Nous posons f(x) = √(2x - 1) et trouvons que f'(x) = 1/(√(2x - 1)). En calculant f'(1.5), nous trouvons f'(1.5) = 1. Donc, la limite de √(2x - 1)/x quand x tend vers 0 est 1.
Enfin, la troisième question demande initialement de calculer la limite de e^x - 1 / x quand x tend vers 1. Cependant, il y a une erreur dans l'énoncé, car il devrait être e^(2x) - 1 / x. Ainsi, en
Maths Spé
Analyse
Terminale
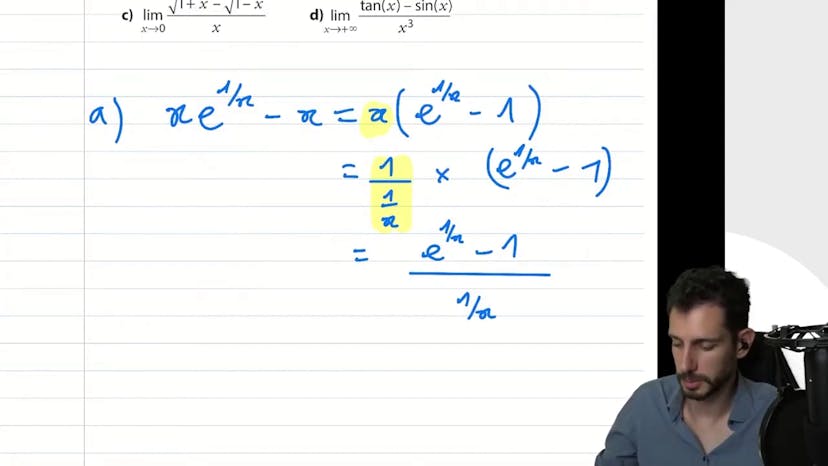
Encore un taux d'accroissement de exp
Dans cette vidéo, le professeur résout un problème de limite mathématique. Il étudie la fonction x exponentiel 1 sur x, moins x, en plus infini. En utilisant des techniques de factoring et de taux d'accroissement, il parvient à simplifier la fonction et à trouver sa limite quand x tend vers plus infini, qui s'avère être 1. Le professeur souligne que des problèmes similaires peuvent être encore plus compliqués et nécessiteront de solides connaissances en mathématiques pour être résolus.


