 All subjects
All subjects
 All subjects
All subjects
Maths Spé
Analyse
Terminale

Introduction Limites
Dans ce cours, on parle de limites de fonctions. Comparé aux limites de suites, qui portent uniquement sur les entiers, les fonctions se portent sur l'ensemble des réels, ce qui rend la tâche plus complexe. On peut parler de limites en l'infini (lorsque X tend vers l'infini), en un réel (lorsque X tend vers un réel spécifique), ou même de limite inexistante (lorsqu'il y a une oscillation infinie). On peut approcher les limites en analysant des graphes, comme celui d'une fonction qui se colle à une valeur réelle, qui tend vers l'infini, ou qui oscille très haut avant/derrière une valeur réelle. Les méthodes d'analyse comprennent une analyse graphique, le calcul de limites et la détermination d'asymptotes horizontales ou obliques. Il est important de comprendre les définitions et de savoir reconnaître les différents types de limites de fonctions.
Maths Spé
Analyse
Terminale

En l'infini, limites finies et infinies
Le cours traite de la notion de limite d'une fonction lorsque la variable x tend vers plus l'infini. Il y a deux définitions à connaître : lorsque la fonction tend vers plus l'infini et lorsque la fonction tend vers un réel L. Pour une fonction qui tend vers plus l'infini, cela signifie que pour tout plateau Y égal à un grand A choisi arbitrairement, la fonction finit toujours par dépasser complètement ce plateau. Pour une fonction qui tend vers un réel L, cela signifie que toutes les valeurs de la fonction finissent toujours par être dans un couloir, quelle que soit la largeur du couloir autour de la limite. Les définitions formelles sont ensuite données, avec des exemples graphiques pour illustrer la notion de couloir. Les définitions peuvent être utilisées pour résoudre des exercices, et il est important de les comprendre pour obtenir de bons résultats dans ce domaine.
Maths Spé
Analyse
Terminale

Les asymptotes horizontales
Découvrez dans cette vidéo les limites de fonction lorsque x converge vers l'infini et ce qu'est une asymptote. Il y aura plusieurs types d'asymptote, mais ici nous allons nous concentrer principalement sur une asymptote horizontale, qui est en fait une droite vers laquelle la courbe de f va venir se coller.Lorsque la limite de f, lorsque x tend vers l'infini, converge vers un réel, que l'on appelle L, la courbe se colle à une droite. Il est important de noter qu'il ne s'agit pas de l'asymptote de la fonction f, mais de celle de sa courbe.Il est possible de se coller à une droite de différentes manières, à la fois croissante et décroissante. Il est également possible d'avoir une asymptote horizontale avec une fonction sinus.En résumé, une asymptote horizontale est une droite vers laquelle la courbe de F se rapproche infiniment proche. C'est une notion liée à la vision assez intuitive qu'on peut avoir de la limite.
Maths Spé
Analyse
Terminale
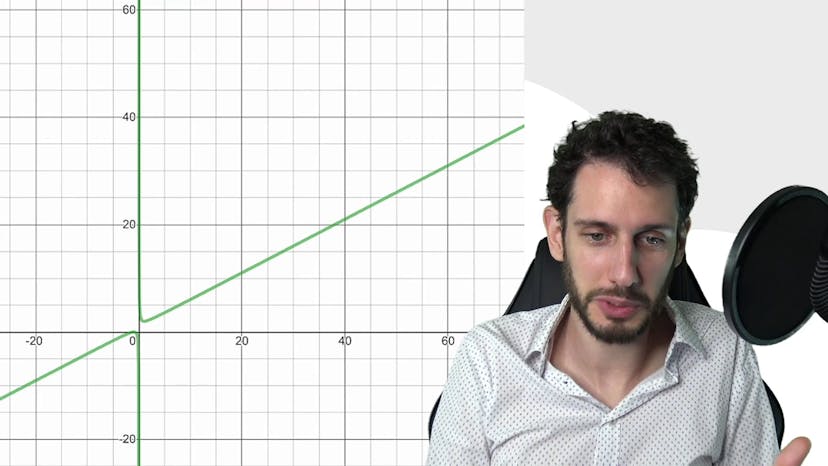
Bonus : Les asymptotes obliques
Dans cette vidéo, on parle de l'asymptote oblique, qui est une droite inclinée qui se rapproche de la courbe d'une fonction dans la direction de plus infini ou moins infini. Lorsque la différence entre la valeur de la fonction et la droite tend vers 0, on dit que la droite est une asymptote oblique à la courbe. Ce concept est important en mathématiques et est souvent utilisé dans les exercices. Une illustration simple est donnée pour montrer comment une courbe tend vers une droite affine en plus infini ou moins infini. L'asymptote horizontale est également une autre question importante qui sera traitée dans une autre vidéo.
Maths Spé
Analyse
Terminale

En un point réel, limite infinie
Le cours aborde les limites de fonction avec x tendant vers un réel a. On distingue deux cas principaux : lorsque f tend vers plus ou moins l'infini et lorsque f converge vers une valeur finie. Les limites sont définies selon la capacité de la fonction à dépasser un plateau donné. La notion de limite à gauche et limite à droite est abordée. La définition de l'asymptote verticale est présentée pour les cas où la limite infinie est atteinte en un point fini.
Maths Spé
Analyse
Terminale

Introduction Convergence
Dans ce nouveau sous-chapitre sur les limites de fonctions, on va aborder des concepts pratiques. Il sera important de connaître par cœur certains tableaux de fonctions de référence, notamment la limite de 1 sur x en plus infini. On étudiera également comment combiner des limites, par exemple, si la fonction f tend vers 1 et la fonction g tend vers 2, quelle est la limite de f plus g ? Il y aura des règles générales à connaître ainsi que des cas particuliers appelés les formes indéterminées, pour lesquels il n'y aura pas de règles préétablies.
On étudiera aussi des théorèmes de convergence, similaires à ceux déjà vus pour les suites. Le théorème des gendarmes, par exemple, où deux fonctions encadrent une troisième fonction et la conduisent vers la même limite. Il y aura également le théorème de comparaison pour les limites infinies, qui permet de déterminer si une fonction est plus grande qu'une autre en se basant sur leurs limites respectives.
On abordera également la croissance comparée, en se concentrant principalement sur l'exponentiel et sa comparaison avec des polynômes. On verra aussi comment gérer les limites des fonctions composées, en décomposant les fonctions complexes en sous-blocs.
En résumé, il sera nécessaire de connaître les tableaux de référence pour les fonctions, les opérations sur les limites, les formes indéterminées, les théorèmes de comparaison, de convergence et de croissance comparée, ainsi que la méthode pour gérer les formes indéterminées. Si on maîtrise ces points, on sera prêt à aborder les problèmes de limites de fonctions.
Maths Spé
Analyse
Terminale

Tableaux : fonctions de référence
Dans cette vidéo, le cours aborde les notions de limites et de règles de combinaison des fonctions de référence. Il commence par évoquer la fonction 1/x, dont la limite est plus l'infini lorsque x tend vers 0 du côté positif, et moins l'infini lorsque x tend vers 0 du côté négatif. Ensuite, les limites des fonctions x^n, où n est un nombre entier positif, sont abordées. On observe que ces fonctions tendent toutes vers plus l'infini lorsque x devient très grand. Cependant, si n est impair, la fonction tend vers moins l'infini lorsque x devient très petit. Ensuite, l'exponentielle et la racine sont étudiées. L'exponentielle de x tend vers plus l'infini lorsque x tend vers plus l'infini, et vers 0 lorsque x tend vers moins l'infini. La racine de x tend vers 0 lorsque x tend vers 0, et 1/racine de x tend vers 0 lorsque x tend vers plus l'infini et moins l'infini. Ces notions sont illustrées à l'aide de graphiques, facilitant leur compréhension. Il est important de retenir ces différentes limites lors de résolutions d'exercices, afin de ne pas se tromper dans les calculs. Le cours se termine en invitant les spectateurs à poser leurs questions dans la FAQ.
Maths Spé
Analyse
Terminale

Tableaux : combiner des limites
Ce cours aborde les limites de Fonctions. Lorsque deux fonctions, f et g, tendent vers les limites L et L', le produit de ces limites est L*L'. Si L est fini alors que la limite de g est soit +infini ou -infini, la limite de la multiplication est soit +infini ou -infini selon le signe de L. Pour les formes indéterminées, il n'y a pas de règle qui s'applique tout le temps. Les deux formes indéterminées à retenir sont 0 fois l'infini et plus l'infini plus moins l'infini. Les fonctions peuvent être combinées en quotient, f/g, et si les deux fonctions tendent vers des limites L et L', la limite du quotient est L/L'. Lorsque le quotient est 0 sur 0, toutes les réponses sont possibles. Lorsque le quotient est plus l'infini sur plus l'infini, toutes les réponses sont possibles également.
Maths Spé
Analyse
Terminale
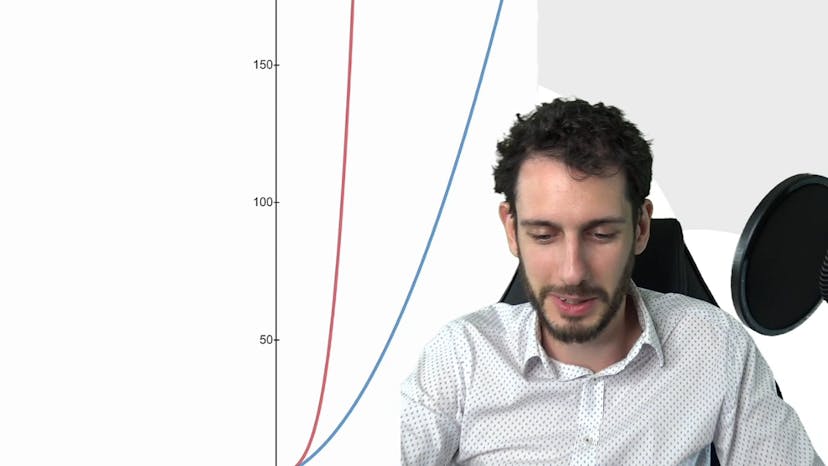
Comparaison et encadrement
Ce cours traite de deux théorèmes qui permettent de comparer et d'étudier des fonctions de manière efficace, sans les étudier en détail. Le premier théorème est celui de la comparaison, qui dit que si une fonction f tend vers l'infini et qu'une autre fonction g est plus grande que f, alors f va pousser g vers l'infini. Le théorème d'encadrement, également appelé "théorème des gendarmes", est le second théorème présenté. Il stipule que si deux fonctions f et h encadrent une fonction g et tendent toutes deux vers la même limite, alors g tend également vers cette même limite. Le cours utilise des exemples pour illustrer ces théorèmes, notamment avec des graphiques pour mieux visualiser les concepts. Ces théorèmes sont particulièrement utiles pour résoudre des exercices de mathématiques impliquant des limites de fonctions.
Maths Spé
Analyse
Terminale
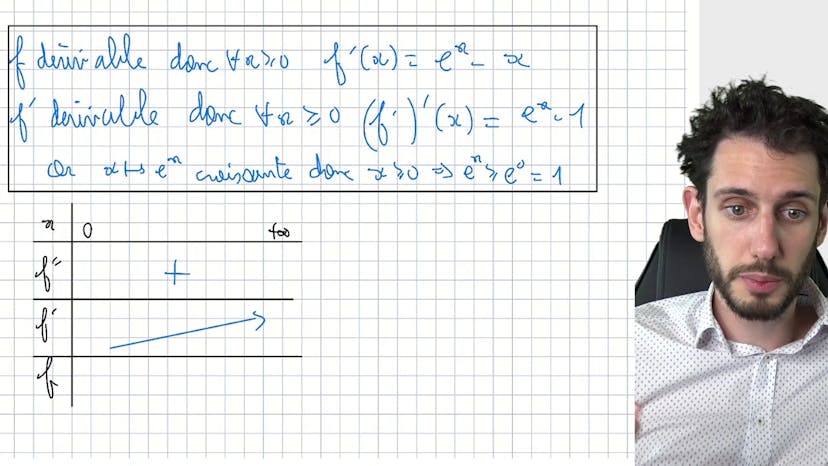
Croissance comparée exp et ln
La croissance comparée est la théorie selon laquelle l'exponentielle l'emporte sur n'importe quelle puissance de x. En d'autres termes, si vous divisez E2x par x puissance n, la limite est toujours l'infini. L'exponentielle domine complètement sur les x puissances n. La propriété des puissances est utilisée pour appliquer cette théorie à l'exponentielle. On utilise également un changement de variable pour démontrer que la quantité tend vers 0 lorsque x tend vers moins l'infini. Cette méthode peut également être utilisée pour trouver des solutions simples à certains calculs de limites.
Maths Spé
Analyse
Terminale

Limite des fonctions composées
Ce cours parle des limites de fonction, plus précisément de la composition de fonctions. L'exemple donné est celui de la limite de la racine de 1+ex lorsque x tend vers l'infini. Pour trouver cette limite, on décompose la fonction en deux parties: 1+ex et la racine de cette fonction. On utilise ensuite un théorème mathématique qui nous autorise à faire cette composition. La limité de la racine est prouvée en utilisant le comportement de la fonction racine envers la limite de 1+ex. Le théorème stipule que si la limite de f(x) tend vers b et que la limite de g(x) tend vers 1 quand f(x) tend vers b, alors la limite de g(f(x)) tend vers 1. En résumé, ce cours explique comment utiliser la composition de fonctions pour trouver des limites, en utilisant un théorème mathématique.
Maths Spé
Analyse
Terminale
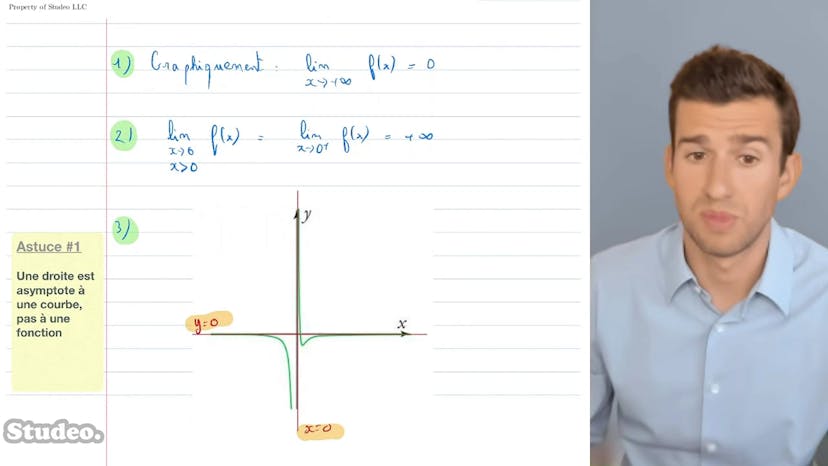
Analyse graphique
Dans ce cours, nous examinons les limites de fonctions en utilisant une analyse graphique. Nous examinons une fonction tracée et déterminons ses limites en examinant son comportement lorsque x tend vers plus ou moins l'infini. En utilisant cette méthode, nous pouvons identifier les asymptotes verticales et horizontales de la courbe. Les équations des asymptotes sont de la forme y = a pour une droite horizontale et x = a pour une droite verticale. Nous faisons également deux remarques: premièrement, une droite est l'asymptote à une courbe, pas à une fonction. Deuxièmement, une droite peut être l'asymptote en deux endroits.


