Online Fonctions : dérivabilité (2) course by Top Instructors - Fonctions : dérivabilité (2)

En construction !

Aucun résumé n'est disponible pour cette vidéo

En construction !

Aucun résumé n'est disponible pour cette vidéo

En construction !

Ce cours est une transcription d'une vidéo sur le chapitre à venir. La patience est de mise car le chapitre sera bientôt disponible.

Définition du nombre dérivé

Aucun résumé n'est disponible pour cette vidéo

Dans ce cours, nous nous intéressons à la dérivabilité en un point lorsque les fonctions ont différentes expressions sur leur ensemble de définition. Nous commençons par l'exemple classique de la fonction sin(x)/x, qui n'est pas définie en zéro car on ne peut pas diviser par zéro. Cependant, cette fonction tend vers 1 lorsque x tend vers zéro, donc nous pouvons "prolonger" la fonction en zéro en posant f(0)=1. Ensuite, nous nous demandons si cette fonction est dérivable en zéro. Pour répondre à cette question, nous utilisons la définition de la dérivabilité et calculons le taux d'accroissement, qui s'avère être 1. Ainsi, la fonction est bien dérivable en zéro. Ensuite, nous étudions deux autres exemples de fonctions avec des expressions différentes sur leur ensemble de définition. Dans le premier exemple, la fonction est x/(1+|x|). Nous remarquons que cette fonction est continue partout sauf en zéro, où |x| n'est pas dérivable. Pour savoir si la fonction est dérivable en zéro, nous devons utiliser la définition et calculer le taux d'accroissement, qui tend vers 1. Par conséquent, la fonction est bien dérivable en zéro. Dans le deuxième exemple, la fonction est xsin(x)sin(1/x), avec g(0)=0. Nous constatons que cette fonction est continue, mais nous devons utiliser la définition de la dérivabilité pour savoir si elle est dérivable en zéro. En calculant le taux d'accroissement, nous obtenons sin(x)sin(x), qui tend vers zéro. Cependant, sin(x) n'a pas de limite, ce que nous prouvons en montrant qu'il existe des valeurs de x pour lesquelles sin(1/x) = 1 ou -1. Par conséquent, nous concluons que la fonction g n'est pas dérivable en zéro. Enfin, nous examinons un dernier exemple, la fonction |x|sin(x). Cette fonction est parfaitement définie, mais |x| n'est pas dérivable en zéro. En utilisant la définition de la dérivabilité, nous calculons le taux d'accroissement, qui tend vers zéro. Par conséquent, la fonction h est dérivable en zéro et h'(0)=0. En résumé, pour déterminer si une fonction est dérivable en un point lorsque les fonctions ont différentes expressions sur leur ensemble de définition, nous devons recalculer le taux d'accroissement en utilisant la définition de la dérivabilité. C'est ainsi que nous pouvons dire si la fonction est dérivable ou non. La question de savoir si la dérivée est continue sera abordée dans d'autres méthodes.

Dérivée n-ième

Dans ce cours, nous apprenons comment appliquer la formule de Leibniz pour calculer les dérivées d'ordre supérieur. Nous prenons comme exemple une fonction produit composée d'un polynôme et d'une exponentielle. Tout d'abord, il est important de justifier que cette fonction est dérivable à l'ordre n. Ensuite, nous appliquons la formule de Leibniz qui dit que la dérivée d'ordre n est égale à la somme des combinaisons possibles entre les dérivées km du polynôme et les dérivées n-km de l'exponentielle. Il faut noter que les dérivées d'ordre supérieur du polynôme sont toutes nulles à partir de la dérivée troisième. Donc, il est plus simple de choisir de dériver n-km fois le polynôme. Finalement, nous simplifions l'expression en factorisant par e^-x et en effectuant les calculs. Il est important de repérer les cas où les dérivées d'une des fonctions deviennent nulles, car cela simplifiera grandement l'expression finale. C'est ainsi que nous maîtrisons et utilisons la formule de Leibniz pour calculer les dérivées d'ordre supérieur.

Utiliser la définition formelle de limite

Le cours porte sur les dérivés et explique la définition formelle de la dérivée comme étant la limite du taux d'accroissement. On applique cette définition à une méthode de base pour calculer la dérivée. Ensuite, on se demande si une limite parfaitement définie implique nécessairement la dérivabilité de la fonction. On utilise une astuce de décomposition du taux d'accroissement pour montrer que la réciproque est fausse. On prend l'exemple de la valeur absolue qui n'est pas dérivable en 0, malgré une limite parfaitement définie qui vaut 0. Ainsi, on montre comment utiliser la définition formelle de la dérivée.

Sens de variation

Aucun résumé n'est disponible pour cette vidéo

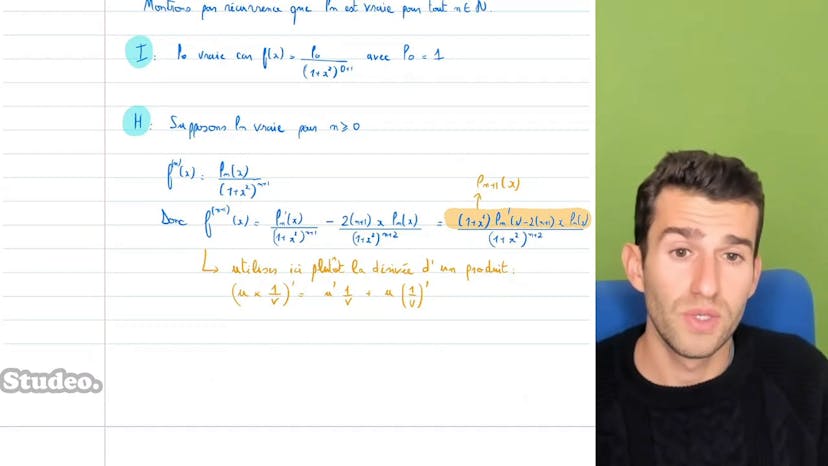
Dérivée n-ième difficile

Dans ce cours, nous étudions la dérivée n-ième d'une fonction en utilisant la formule de Leibniz. Nous cherchons à trouver des relations récursives entre les dérivées n-ièmes successives. La question principale est de savoir à quoi ressemble la dérivée n-ième de la fonction f(x) = e^x + x^2. Nous voulons montrer que cette dérivée peut être exprimée sous la forme d'un polynôme Pn(x) = 1 + x^2)^n+1. Pour cela, nous utilisons une récurrence et nous essayons de trouver une relation entre Pn+1(x) et Pn(x) en utilisant la dérivée de Pn(x). Il s'avère que trouver directement Pn(x) est fastidieux, mais nous trouvons une relation en dérivant n fois la fonction f(x) et en simplifiant les termes. En utilisant la formule de Leibniz, nous trouvons une expression plus simple pour Pn'(x) en fonction de Pn-1(x). Après avoir initialisé la récurrence et montré l'hérédité, nous dérivons l'expression de Pn+1(x) et simplifions les termes. Finalement, nous obtenons une expression pour Pn'(x) en utilisant la formule de Leibniz. En dérivant l'expression n fois, nous trouvons que la dérivée n-ième de f(x) est égale à une somme de termes impliquant Pn(x), Pn-1(x) et Pn-2(x). En remplaçant les expressions de Pn+1(x), Pn(x) et Pn-1(x), nous obtenons une relation finale entre Pn'(x) et Pn-1(x). Bien que les calculs puissent paraître complexes, la formule de Leibniz avec des polynômes nous permet de simplifier les termes jusqu'à obtenir des relations claires entre les dérivées n-ièmes successives.

Tangente commune

Ce cours traite des tangentes et de l'utilisation de la dérivée. L'exercice présenté concerne deux courbes, y égal x carré et y égal 1 sur x, et l'objectif est de montrer qu'elles ont une tangente commune. Il est important de noter que tangente commune ne signifie pas qu'elles sont tangentes au même point, mais plutôt qu'elles partagent une droite commune, avec le même coefficient directeur et la même ordonnée à l'origine. Pour cela, il est nécessaire d'obtenir l'expression générale des tangentes pour chacune des courbes. En utilisant la dérivée, on obtient les équations des tangentes. En résolvant les équations, on trouve qu'il y a une seule tangente commune avec une abscisse de -2 et une ordonnée de -1,5. L'équation de cette droite est y égal moins 4x moins 4. Ce cours met en évidence l'importance de bien comprendre et maîtriser les notions de tangentes et de dérivées.

Théorème de Rolle

Dans ce cours, nous allons voir comment utiliser le théorème de Rolle de manière efficace. Le théorème de Rolle se présente sous forme d'exercices, notamment avec une petite astuce pas facile à comprendre. Pour commencer, nous considérons une fonction f définie sur un intervalle i, de classe Cn, qui s'annule en n plus un point distinct de i. Nous voulons montrer que la dérivée n s'annule au moins une fois sur i, puis que la dérivée n-1 de f'αf s'annule également au moins une fois sur i. La première méthode consiste à utiliser la récurrence. Nous démontrons la propriété suivante pk : la dérivée km s'annule n plus une moins k fois au moins sur i. Pour l'initialisation, nous n'avons pas de problème. Par hypothèse, fk s'annule n plus une moins k fois. Nous voulons montrer que la dérivée k plus unième s'annule n moins k fois au moins. Nous appliquons le théorème de Rolle sur chaque intervalle ij défini par les points αj et αj plus 1. Ainsi, nous avons n moins k intervalles sur lesquels la dérivée s'annule au moins une fois. En utilisant le théorème de Rolle, nous démontrons que fk plus 1 s'annule au moins n moins k fois. Cette démonstration par récurrence fonctionne parfaitement. Pour la question 2, nous introduisons une fonction h qui est égale à f de x multiplié par e de alpha x. En dérivant h, nous obtenons h prime qui est égal à f prime plus alpha f fois e de alpha f. L'astuce ici est que nous pouvons appliquer le théorème de Rolle sur chaque point où h s'annule, car si h prime s'annule au moins une fois, cela signifie que le terme f prime plus alpha f s'annule également au moins une fois. En utilisant les hypothèses précédentes, nous appliquons le théorème de Rolle et retrouvons que la dérivée enième de f prime plus alpha f s'annule au moins une fois. Ainsi, nous pouvons utiliser le théorème de Rolle dans des exercices en utilisant une petite astuce pour simplifier la démonstration.