Online Learning Courses

Trouver l'équation d'un plan avec un vecteur normal

Dans ce cours, nous apprenons comment déterminer si trois points ABC définissent un plan dans l'espace. La seule condition pour que les points ne définissent pas un plan est qu'ils soient alignés. Pour éviter cela, nous pouvons vérifier si deux vecteurs formés par les points ABC sont collinéaires ou non. Nous proposons de calculer le vecteur AB et de voir s'il est égal à -AC. Si cela est le cas, alors les points sont alignés et ne définissent pas un plan. Par conséquent, il est important de vérifier les collinéarités lors de ce type d'exercices de géométrie pour éviter les fausses pistes. Ensuite, nous abordons la détermination d'une équation cartésienne du plan défini par les trois points ABC. Pour cela, nous cherchons d'abord un vecteur normal au plan. Ensuite, nous utilisons les produits scalaires entre le vecteur normal et les vecteurs AB et AC pour obtenir deux équations. Ces équations nous permettent de trouver une famille de vecteurs normaux possibles pour le plan. Ensuite, nous pouvons choisir un vecteur normal spécifique pour obtenir l'équation cartésienne du plan. En résumé, pour déterminer si trois points définissent un plan, nous vérifions les collinéarités des vecteurs formés par ces points. Pour trouver l'équation cartésienne du plan, nous cherchons d'abord un vecteur normal en utilisant les produits scalaires, puis nous obtenons une famille de vecteurs normaux possibles avant de choisir un vecteur spécifique. Il est important d'aborder ces exercices avec une approche méthodique pour éviter les fausses pistes et trouver rapidement les résultats attendus.

Trouver un angle avec le produit scalaire

Dans ce cours, nous avons un cube avec un point O comme centre. L'objectif est de trouver l'angle entre les deux diagonales AG et OF, arrondi à 0,0,1 degré. Pour résoudre ce problème, nous pouvons utiliser la formule du produit scalaire avec le cosinus. Le produit scalaire nous permettra de trouver l'angle recherché. En utilisant des coordonnées, nous pouvons considérer le cube comme un espace en trois dimensions. Les points intéressants dans ce repère sont AD, AE, AG et F. En notant les coordonnées de ces points, nous obtenons: - D : 0 sur AB, 1 sur AD, 0 sur AE - G (opposé de D) : 1 sur AB, 1 sur AD, 1 sur AE - F : 1 sur AB, 0 sur AD, 1 sur AE Ensuite, nous pouvons calculer les vecteurs AG et DF. AG est identique à G, soit 1, 1, 1. DF est calculé en soustrayant les coordonnées de F et de D, soit 1-0, 0-1, 1-0, ce qui donne 1, -1, 1. Nous pouvons également calculer les normes de AG et DF, qui sont toutes les deux égales à racine de 3. En utilisant l'équation du produit scalaire, nous remplaçons AG.DF par la norme de AG multipliée par la norme de DF par le cosinus de l'angle FOG. En effectuant les calculs, nous obtenons le résultat de l'angle recherché, que nous arrondissons à 0,01° près. Il est important de prendre l'initiative de poser un repère et de réaliser les calculs nécessaires pour trouver l'angle.

Distance d'un point à un plan

Le cours porte sur la méthode classique pour déterminer la distance entre un point et un plan dans l'espace. La distance minimale entre le point et le plan est appelée distance entre un point et un plan. Cette distance est calculée en faisant une projection orthogonale du point sur le plan. La formule de la distance entre un plan et un point est donnée par |Ax + By + Cz + D| / √(A^2 + B^2 + C^2), où A, B, C et D sont des coefficients spécifiques au plan et x, y, z sont les coordonnées du point. Pour trouver cette distance, il faut également trouver les coordonnées exactes du point projeté orthogonal du point sur le plan. Les coordonnées du point projeté sont trouvées en utilisant des conditions spécifiques, notamment que la droite reliant le point et le point projeté est parallèle au vecteur normal du plan, et que le point projeté appartient au plan. En utilisant ces conditions, les coordonnées du point projeté peuvent être trouvées en fonction d'un facteur de proportionnalité lambda. En substituant ces coordonnées dans la formule du plan, on peut alors trouver la distance entre le point et le plan.

Distance entre deux droites non coplanaires

Dans cet exercice, il est demandé de trouver une représentation paramétrique pour deux droites, de montrer qu'elles ne sont pas coplanaires, de vérifier que certains points appartiennent à ces droites, de démontrer que la droite HK est perpendiculaire aux deux droites, et enfin de calculer la distance entre les deux droites. Pour commencer, on considère une droite définie par un point et un vecteur directeur. On peut utiliser une méthode basique pour trouver une équation paramétrique de cette droite. Ensuite, on fait de même pour une autre droite définie par un autre point et un autre vecteur directeur. On obtient ainsi les équations paramétriques pour les deux droites. Ensuite, on montre que les droites ne sont pas coplanaires, c'est-à-dire qu'elles ne sont ni parallèles, ni n'ont de point d'intersection. On peut le démontrer en montrant que les vecteurs directeurs des droites ne sont pas parallèles. De plus, on peut supposer qu'il existe un point d'intersection et aboutir à une contradiction en cherchant des valeurs de paramètres qui satisfont à toutes les équations. Ainsi, on conclut que les droites ne sont pas coplanaires. On vérifie également que certains points appartiennent bien aux droites, en utilisant les équations paramétriques et en trouvant des valeurs de paramètres qui satisfont les conditions données. Ensuite, on démontre que la droite HK est perpendiculaire aux deux droites en montrant que le produit scalaire entre le vecteur directeur de chaque droite et le vecteur HK est nul. On obtient ainsi une perpendiculaire commune aux deux droites. Enfin, la distance entre les droites est définie comme la distance entre les points H et K, ce qui correspond à la norme du vecteur HK. On effectue les calculs et on obtient la valeur de la distance entre les droites. Cet exercice peut sembler un peu long, mais il est réalisable en suivant les étapes décrites et en utilisant les équations paramétriques des droites pour trouver les informations demandées.

Trouver un plan avec 3 points

Dans ce cours, nous apprenons deux méthodes pour trouver une équation cartésienne d'un plan passant par un certain point avec un vecteur normal donné. La première méthode consiste à utiliser une équation générale du type "ax + by + cz + d = 0", où les coordonnées x, y et z sont déterminées par le vecteur normal abc. Cette méthode est utilisée de manière instinctive et ne requiert pas une démonstration formelle. La deuxième méthode, que je préfère, implique de comprendre la définition profonde d'un vecteur normal. Un plan est défini par un point donné et un vecteur normal qui est orthogonal au plan. Ainsi, tout point situé dans le plan a un vecteur gm, reliant le point m au point donné, qui est orthogonal au vecteur normal. En utilisant la propriété que deux vecteurs sont orthogonaux si leur produit scalaire est nul, nous pouvons écrire une équation du type "x-1 * 0 + y-1 * (-3) + z-1 * 5 = 0" pour trouver l'équation cartésienne du plan. En résumé, il existe deux méthodes pour trouver une équation cartésienne d'un plan. La première méthode est basée sur une équation générale, tandis que la deuxième méthode s'appuie sur la compréhension de la définition d'un vecteur normal.

Méthode classique de géométrie dans l'espace

En résumé, ce cours de géométrie porte sur la démonstration que le triangle DHM est rectangle, dans un cube ABCD de côté A, avec le point M comme milieu du segment AB. Le raisonnement pour prouver cela est assez simple, en montrant que DH est un vecteur normal pour le plan ABC, c'est-à-dire la phase d'en bas. Ensuite, l'exercice consiste à déterminer la valeur de l'angle DMH en degrés, arrondi à 0,01 près. Il est possible de calculer le produit de MH avec MD pour obtenir l'angle, mais il est plus simple de constater que l'on a un triangle rectangle. On peut donc utiliser la formule de la tangente pour calculer l'angle recherché, en prenant le rapport de DH sur DM. Peu importe la mesure du côté du cube, la longueur du côté n'intervient pas dans l'expression de l'angle, car tous les cubes semblables ont le même angle. En utilisant la formule de la tangente, on peut trouver la valeur de l'angle en calculant l'arc tangente ou en utilisant la fonction tangente inverse.

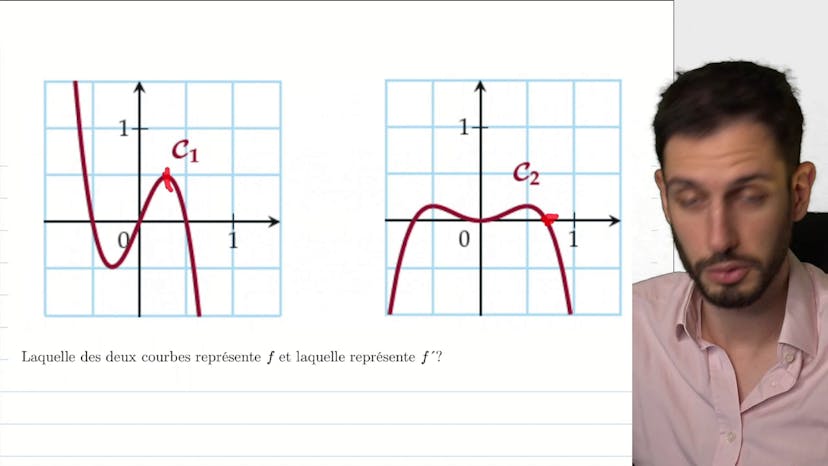
Qui est f qui est f' sur un graphique ?

Ce cours explique la relation entre une fonction et sa dérivée. Lorsqu'une fonction est dérivable, elle est croissante si sa dérivée est positive et décroissante si sa dérivée est négative. Pour analyser deux graphes et déterminer lequel représente la dérivée, il suffit d'observer le signe de chaque fonction. Si la première fonction est positive jusqu'à (-0,5) et croit jusqu'à (-0,5), et que la seconde fonction est négative jusqu'à 0 et décroît jusqu'à 0, alors la première fonction est la dérivée. En revanche, si la première fonction est négative jusqu'à (-0,6) mais la seconde fonction décroît jusqu'à (-0,1), cela ne correspond pas à une dérivée. De plus, si la première fonction est positive de (-0,6) à 0, il faudrait qu'elle croisse entre les deux, ce qui n'est pas le cas. Finalement, si la première fonction devait décroître uniquement à partir de 0,7, cela ne correspondrait pas non plus. En conclusion, pour une fonction dérivable, on peut déterminer si elle croît ou décroît en observant le signe de sa dérivée.

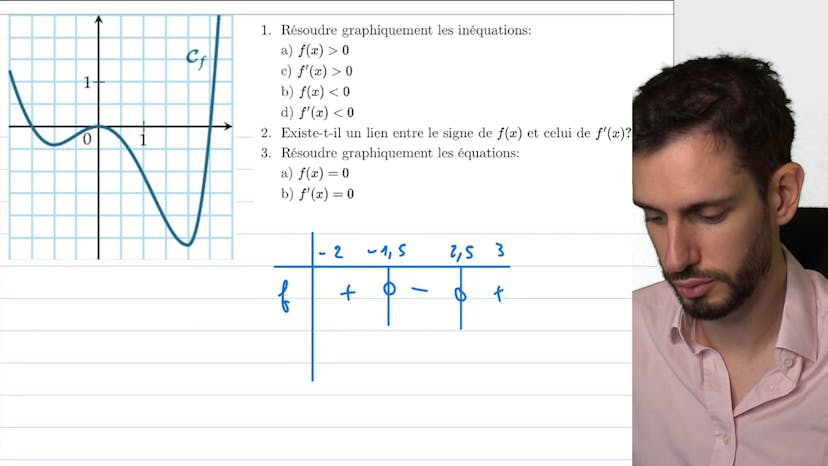
Lien entre signe de f et de f' ?

Ce cours aborde la résolution graphique des inéquations et met en évidence le lien entre la positivité de la fonction f(2x) et la croissance de sa dérivée f'(2x). Nous examinons les différentes régions où f(2x) est positif et négatif, ainsi que le signe de f'(2x) dans ces régions. Nous constatons qu'il n'y a pas de lien direct entre le signe de f(2x) et celui de f'(2x). Ensuite, nous résolvons graphiquement les équations f(2x) = 0 et f'(2x) = 0 en identifiant les points où la courbe touche l'axe des x et les points où la tangente à la courbe a une pente nulle. L'idée principale de cet exercice est de ne pas confondre les notions de positivité de la fonction et de sa dérivée, et de comprendre que différents scénarios sont possibles en termes de croissance de la fonction et du signe de sa dérivée.

Méthode COMPLETE pour étudier une fonction

En étudiant une fonction, il y a plusieurs étapes à suivre pour s'en sortir. Tout d'abord, il faut toujours vérifier l'ensemble de définition et faire attention aux racines et aux fractions. Ensuite, il est important de vérifier si la fonction est paire ou impaire, ce qui permet de simplifier l'étude. Si cela n'est pas possible, il est conseillé de vérifier si la fonction est trivialement croissante ou décroissante, car cela peut permettre de gagner du temps. Si cela ne fonctionne pas, il faut déterminer l'ensemble de dérivabilité et calculer la dérivée de la fonction. Il est ensuite important de déterminer le signe de la dérivée en fonction de x et de faire un tableau de variation en conséquence. Enfin, il est possible que des questions supplémentaires sur la convexité, les limites ou le tracé soient posées. En suivant cette méthode, il est possible de bien mener une étude de fonction et de ne pas se tromper.

Etude classique : une fonction inverse

Ce cours explique comment étudier une fonction typique en calcul différentiel. La fonction h est définie partout sur 5 par h2x égale 7-10 sur 5-x, et il faut justifier qu'elle est dérivable sur cet ensemble et déterminer sa fonction dérivée h'. Pour toute x différent de 5, h' de x est négatif strict, car il est égal à -10 divisé par un carré positif. Enfin, on peut dresser un tableau de variations de la fonction h en excluant la valeur interdite 5 et en notant que h' est toujours négatif et décroissant.

Etude classique : fonction cube

Dans ce cours, on étudie une fonction polynôme du troisième degré qui est dérivable sur R. On calcule la dérivée de cette fonction et on étudie son signe en utilisant les automatismes qui doivent être maîtrisés. Ensuite, on calcule les racines du polynôme et on détermine les variations de la fonction. Le cours insiste sur l'importance de connaître les polynômes du second degré car ce type d'exercice est très fréquent en mathématiques.