Online Révisions Maths lycée Courses by Top Instructors

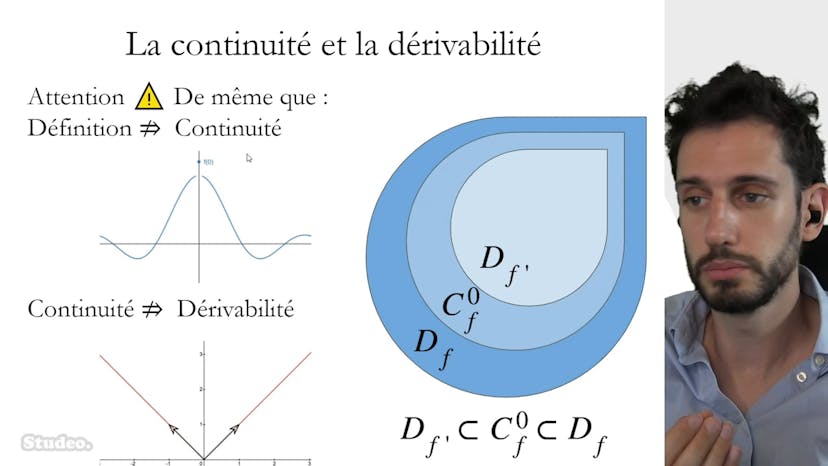
Continuité vs dérivabilité

Ce cours explique le lien entre dérivabilité et continuité. Il démontre que si une fonction est dérivable en un point, alors elle est continue en ce point. Cependant, le contraire n'est pas vrai. La démonstration utilise la définition de la dérivabilité d'une fonction f en un point A, qui donne la limite du taux d'accroissement de f quand x tend vers A. En utilisant cette expression, on peut isoler f de x et prendre la limite quand x tend vers A. Cela conduit à la conclusion que la limite de f de x quand x tend vers A égale f de A, ce qui est la définition de la continuité en ce point. Il est également souligné que la définiabilité n'implique pas la continuité, et la continuité n'implique pas la dérivabilité. Des exemples de fonctions non dérivables mais continues sont donnés, tels que la racine carrée en 0 et la valeur absolue. En résumé, l'ensemble des x où la fonction est dérivable est inclus dans l'ensemble des x où la fonction est continue, qui est lui-même inclus dans l'ensemble des x où la fonction est définie.

Continuité et suites : Théorème du point fixe

L'étude de la continuité dans le domaine des suites est très importante, et l'un des théorèmes fondamentaux est le théorème du point fixe. Ce théorème stipule que si une fonction f continue est définie sur un intervalle i, et qu'une suite un est définie de telle manière que pour tout n, un est dans i et un+1 est égal à f(un), alors si un converge vers l, où l est dans i, cela implique que f(l) = l. Ce résultat est intuitif car lorsque nous disons que la limite de f(x) lorsque x tend vers a est égale à f(a), cela nécessite la continuité de la fonction. Dans le théorème du point fixe, la suite un joue le rôle de x dans la définition de la continuité. Ainsi, si un tend vers l, alors la limite de f(un) est égale à f(l). Grâce à l'unicité de la limite, on peut conclure que l = f(l). La démonstration du théorème du point fixe consiste à montrer que si un converge vers l, alors un+1 et f(l) convergent également vers l. En utilisant la continuité de f, on peut affirmer que la limite de f(x) lorsque x tend vers l est égale à f(l). En combinant ces résultats, on peut conclure que l = f(l). En plus du théorème du point fixe, il est également important de mentionner que les comportements de convergence peuvent varier en fonction des propriétés de la fonction f et de la suite un. Par exemple, si f est une fonction continue mais croissante, et que la suite un est décroissante, la convergence peut prendre différentes formes, comme une approche en escalier ou en escargot vers le point d'intersection entre la fonction et la droite y = x. En conclusion, l'étude de la continuité dans le domaine des suites est essentielle, et le théorème du point fixe est un résultat clé dans ce domaine. Il nous permet de comprendre comment les limites des termes d'une suite convergente sont liées à la fonction continue qui la génère.

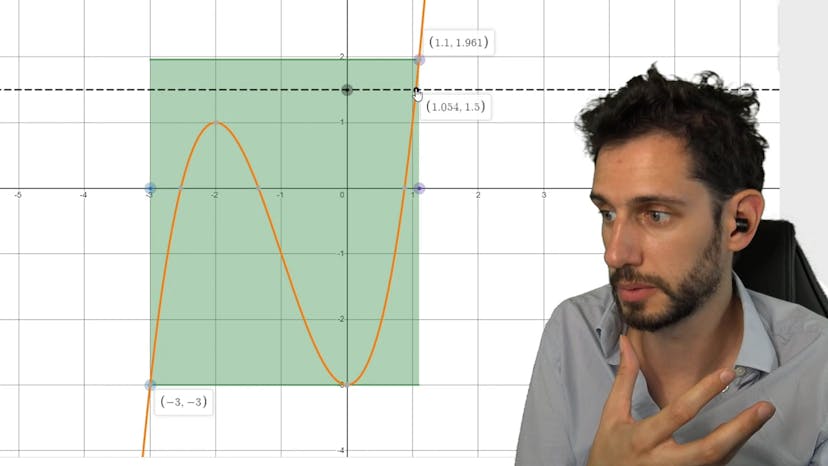
TVI : LE théorème

Le théorème des valeurs intermédiaires est un théorème capital en mathématiques, notamment pour les études de fonctions et la résolution d'équations. Il stipule que pour une fonction continue sur un intervalle donné, toute valeur comprise entre les images de deux points de l'intervalle aura au moins une solution correspondante dans cet intervalle. Ce théorème est illustré à l'aide d'un graphe montrant une courbe continue qui relie les points d'images correspondants des points de l'intervalle. En traçant une droite horizontale représentant une valeur k quelconque entre les images des points a et b, on constate qu'elle croise forcément la courbe, prouvant ainsi l'existence de solutions à l'équation f(x) = k. Ce résultat est valable même si la fonction ne fait que monter ou descendre de manière continue sans variation. Dans ce cas, il n'y aura qu'une seule solution à l'équation. Ce théorème permet de justifier l'existence de solutions dans différents cas et de les localiser. Il est important de l'appliquer en citant le théorème et en précisant si la fonction est continue ou strictement croissante/décroissante.

Continuité en un Point

Dans ce cours, nous examinons comment trouver la dérivée d'une fonction qui a plusieurs expressions sur différents intervalles. Nous constatons qu'elle peut ne pas être dérivable, bien qu'elle puisse être continue. Par exemple, pour la fonction f avec trois expressions selon les intervalles, nous vérifions si elle est parfaitement continue. La première condition pour qu'une fonction soit continue est qu'elle soit définie. Si elle n'est pas définie, il est inutile de poursuivre. Dans notre cas, elle est bien définie. Ensuite, excepté aux limites entre les intervalles, elle est continue sur les intervalles moins l'infini, 3, 3, 5 et 5 plus l'infini. Nous devons donc nous concentrer sur la continuité aux points 3 et 5 qui correspondent aux extrémités de ces intervalles. Comme nous avons deux expressions différentes à gauche et à droite de 3, nous devons vérifier la limite de x tendant vers 3 avec x inférieur à 3 et la limite de x tendant vers 3 avec x supérieur à 3. Ces limites doivent être égales et égales à f de 3 pour avoir la continuité. Dans notre cas, lorsque x tend vers 3 avec x inférieur à 3, nous utilisons la première expression, moins x plus 6. Lorsque x est supérieur à 3, nous utilisons également moins x plus 6. De plus, f de 3 vaut 3. Donc toutes les conditions requises pour que la fonction soit continue en 3 sont remplies. Ensuite, nous faisons la même chose pour 5. Nous examinons la limite lorsque x tend vers 5 avec x inférieur à 5 et la limite lorsque x tend vers 5 avec x supérieur à 5, et nous constatons que ce ne sont pas les mêmes expressions. Dans un cas, cela donne 7 et dans l'autre cas, cela donne 0, tandis que f de 5 vaut 0. Dès que la limite à droite n'est pas égale à la limite à gauche, la fonction ne peut pas être continue. Donc elle n'est pas continue en 5. Maintenant que nous avons examiné la continuité, les prochaines étapes consisteront à examiner la dérivabilité dans les méthodes suivantes.

Dérivabilité en un Point

Le cours porte sur la dérivabilité de la fonction valeur absolue. Il explique que la valeur absolue n'est pas dérivable en 0 car elle a une pente différente à gauche et à droite de ce point. Ensuite, il introduit une fonction qui comprend la valeur absolue, notée f(x) = |x|^2 + 2x - 3. Il explique que cette fonction est continue sur l'ensemble des réels car elle est composée d'un polynôme et de la fonction valeur absolue, qui sont toutes les deux continues. Cependant, en raison de la valeur absolue, la fonction présente une discontinuité de pente en -3 et en 1, ce qui la rend non dérivable en ces points. En observant graphiquement, on constate que la fonction n'est pas dérivable en -3 et 1, mais qu'elle est dérivable sur tous les autres points de l'ensemble des réels, à l'exception de ces deux points. Ce constat n'est pas une preuve formelle, mais simplement une observation. Cela conclut le premier aperçu des composés avec la fonction valeur absolue.

Prolongement par Continuité

Le prolongement par continuité est utilisé lorsque nous avons une fonction qui n'est pas définie en un point, mais dont la limite existe et est finie. Dans ce cas, nous pouvons prolonger la fonction en ce point en posant sa valeur égale à la limite de la fonction lorsque x tend vers ce point. Par exemple, si nous avons une fonction f(x) = x/x, qui n'est pas définie en 0, nous pouvons prolonger la fonction en posant f(0) = 1, ce qui rend la fonction définie et continue en ce point. Dans l'exercice présenté, nous avons une fonction f(x) = x*sin(1/x), qui est définie pour toutes les valeurs de x sauf en 0 à cause du terme 1/x. Nous devons vérifier si cette fonction est bien un prolongement par continuité. En traçant la fonction sur une calculatrice, nous constatons qu'elle semble se rapprocher de 0 en 0. Pour le prouver, nous utilisons l'encadrement du sinus (qui est compris entre -1 et 1) en multipliant la fonction par la valeur absolue de x. En utilisant le théorème de l'encadrement, nous démontrons que la limite de la fonction est bien égale à 0. Ainsi, nous prouvons que la fonction f(x) = x*sin(1/x) est un prolongement par continuité avec f(0) = 0. C'est donc une méthode utilisée pour prolonger une fonction définie sur un ensemble de valeurs à un point où elle n'est pas définie, en la rendant continue. Si vous avez d'autres questions, n'hésitez pas à les poser dans la FAQ.

TVI et Fonction Auxiliaire

Le cours aborde le théorème des valeurs intermédiaires, en utilisant une fonction compliquée comme exemple. La fonction étudiée est f(x) = (10x)/(e^x + 1). L'ensemble de définition est [0,+∞) car le dénominateur est toujours strictement positif. La fonction est définie et dérivable sur cet ensemble. La dérivée de f(x) est obtenue en utilisant la formule du quotient de dérivées. On factorise ensuite cette expression pour obtenir une fonction g(x) = (1-x)e^x. On étudie les signes de g(x) pour appliquer le théorème des valeurs intermédiaires. On trouve que g(x) est strictement décroissante sur [0, +∞), passant de 2 à -∞. Donc, il existe un unique réel α tel que g(α) = 0. Pour déterminer α de manière plus précise, on utilise une calculatrice pour encadrer sa valeur entre 1,28 et 1,29. Ensuite, on utilise les signes de g(x) pour déterminer les variations de f(x). On trouve que f(x) est croissante sur [0, α] et décroissante sur [α, +∞). Les limites de f(x) sont calculées : f(0) = 0 et lim(x→+∞) f(x) = 0. Donc, la fonction f(x) est strictement croissante jusqu'à α où elle atteint un maximum, puis décroît progressivement vers une asymptote horizontale y = 0. La stricte monotonie de la fonction est essentielle pour l'application du théorème des valeurs intermédiaires et l'unicité de l'antécédent. Un contre-exemple est donné pour illustrer ce point. La méthode complète est résumée avec les clés pour réussir ce type d'exercice. Si des questions subsistent, il est recommandé de consulter la FAQ.

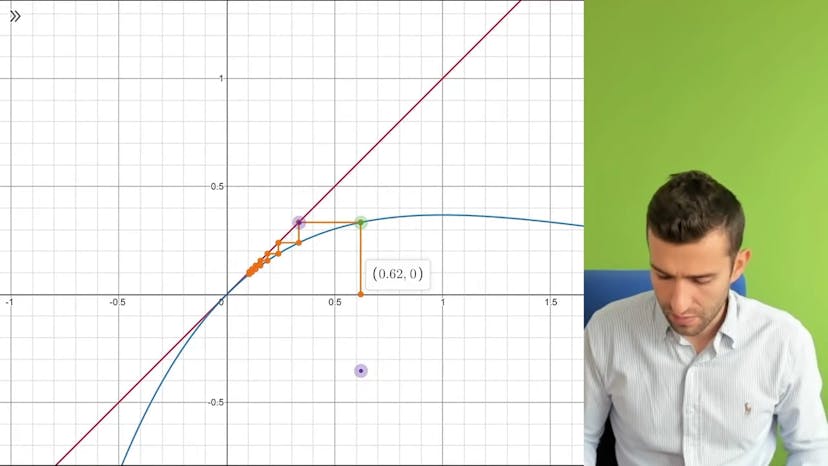
Continuité et suites 1

Dans cette vidéo, nous étudions la méthode pour calculer la limite d'une suite définie par récurrence. Nous examinons les hypothèses nécessaires pour trouver et justifier correctement la limite. Nous utilisons la suite spécifique définie par u0 = 1 et un+1 = u*n – 1. Il est important de noter que la convergence peut dépendre du premier terme de la suite. Si une suite définie par récurrence du type un+1 = f(un) converge vers une limite L, alors un+1 converge également vers L. Pour trouver la limite, nous prenons la limite de l'égalité un+1 = f(un) en passant à la limite des termes. Nous obtenons l'équation f(L) = L, où L est un point fixe solution de cette équation. Cependant, cette méthode n'est valable que si la fonction f est continue. Il est essentiel de justifier la continuité dans cette méthode. Nous admettons dans l'énoncé que la suite converge vers L, et cela nous permet de supposer qu'elle a un point fixe, qui est l'unique limite possible. La représentation graphique de la suite en escalier converge vers 0, mais il est crucial de noter que la convergence dépend du premier terme u0. Si u0 est négatif, la suite divergera vers moins l'infini. Donc, u0 doit être positif pour que la suite converge. Il est également important de souligner que si la fonction f2x = x*e^2-x est discontinue, cette méthode ne fonctionne pas. Nous illustrons cela avec une fonction constante qui change brusquement en un point a. Dans ce cas, nous trouvons une suite spécifique qui converge vers a sans jamais atteindre a. Cette fonction n'est pas continue car la limite de f(un) est différente de f(L), où L est la limite de la suite. Ainsi, la continuité est essentielle dans cette méthode pour trouver et justifier correctement la limite.

Continuité et Suites 2

Ce cours traite de la méthode pour étudier la limite d'une suite définie par récurrence. Tout d'abord, la suite est associée à une fonction f telle que un+1 = f(un). La première étape est donc d'étudier la continuité de f, car elle sera nécessaire pour la suite du traitement. Ensuite, on résout l'équation f(x) = x pour trouver les éventuelles limites de la suite. Ensuite, on étudie la dérivabilité de la fonction f et sa croissance sur les intervalles où elle est définie. Il est important de noter que f peut ne pas être définie sur certains intervalles, ce qui peut impacter son comportement. Ensuite, on applique le principe de récurrence pour démontrer certaines propriétés de la suite, telles que son ordre de croissance et le fait qu'elle soit bornée. En utilisant ces propriétés, on peut conclure que la suite converge vers une limite L. Enfin, on utilise la continuité de f pour montrer que cette limite est également une solution de l'équation f(x) = x. La continuité de f est cruciale pour s'assurer que la limite recherchée appartient à l'ensemble des solutions de cette équation. En résumé, ce cours explique comment trouver la limite d'une suite définie par récurrence en étudiant la fonction associée, ses propriétés de continuité et de croissance, ainsi que l'application du principe de récurrence.

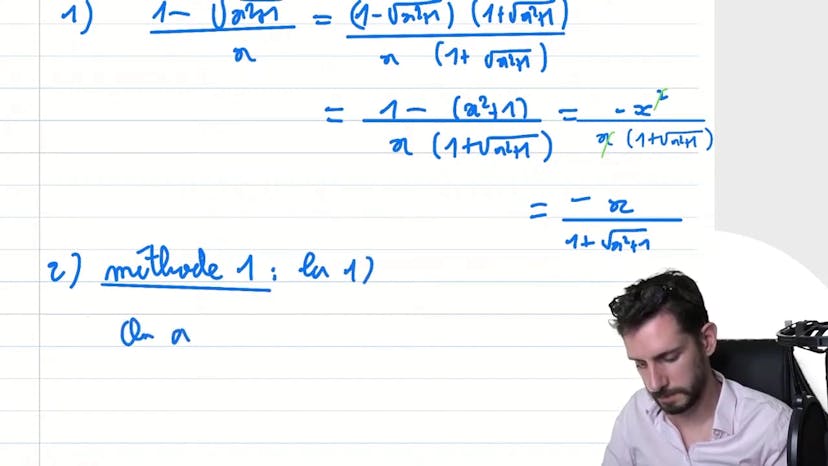
Saut de continuité

Le cours traite de la continuité d'une fonction définie par morceaux. On commence par introduire un exercice simple sur la continuité qui rappelle la définition de la continuité. Ensuite, on donne une fonction définie par f2x égale à une certaine valeur si x est différent de 0, et f2z égale à m si x vaut 0. On explique qu'il est possible d'écrire cette fonction sous une forme différente en utilisant la quantité conjuguée. On présente deux méthodes pour résoudre l'exercice. La méthode 1 consiste à utiliser la quantité conjuguée pour éliminer une forme indéterminée dans la limite de la fonction. La méthode 2 consiste à reconnaître un taux d'accroissement et à utiliser la dérivabilité de la fonction racine pour résoudre l'exercice. On conclut en disant que pour que la fonction f soit continue en 0, il faut que la valeur m soit égale à 0.

TVI et expo

Dans cette leçon, nous étudions le nombre de solutions de l'équation E-x² = E2x-1. Graphiquement, nous avons représenté les deux fonctions E-x² et E2x-1. La première est une courbe en cloche symétrique par rapport à l'axe des ordonnées, tandis que la deuxième est une fonction exponentielle décalée de 1 vers le bas. En examinant le graphique, nous observons qu'il y a une solution autour de 0.552. De plus, pour les nombres négatifs, la fonction E-x² est toujours supérieure à la fonction E2x-1, tandis que pour les nombres positifs, il y a un point d'intersection où les deux fonctions se croisent. Afin de démontrer mathématiquement ces observations, nous séparons l'étude en deux cas : R- (les nombres négatifs) et R+ (les nombres positifs). Pour les nombres négatifs, nous montrons que la fonction E-x² est strictement supérieure à la fonction E2x-1, en utilisant le fait que E2x-1 est négatif. Ainsi, il n'y a pas de solution à l'équation pour les nombres négatifs. Ensuite, pour les nombres positifs, nous étudions la fonction f2x = E-x² - E2x-1. Nous montrons que cette fonction est strictement décroissante sur l'intervalle [0, +∞] en utilisant les propriétés des fonctions exponentielles. Nous montrons également que la limite de f2x quand x tend vers +∞ est -∞. En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe une unique solution à l'équation pour les nombres positifs. En résumé, il n'y a pas de solution à l'équation pour les nombres négatifs, et il y a une unique solution pour les nombres positifs.