Cours de Primitives et EDL en Ligne par les Meilleurs Professeurs - Primitives et EDL

Introduction ED

Une équation différentielle est une équation dont l'inconnue est une fonction. On utilise généralement la variable "x" pour les équations avec des réels, mais pour les équations différentielles, on utilise la variable "y" pour les fonctions. Une primitive "f" est une fonction qui, lorsqu'elle est dérivée, donne la petite fonction "y". Les solutions de l'équation différentielle sont les fonctions qui satisfont cette condition. On peut rencontrer des équations différentielles en physique, par exemple lorsqu'on étudie la trajectoire d'un boulet ou le refroidissement d'une boisson chaude. Ces équations permettent de comprendre comment la vitesse ou la température évolue en fonction de la position ou de la valeur. On peut résoudre les équations différentielles en utilisant des méthodes telles que la méthode des solutions homogènes, la méthode des solutions linéaires simples, ou la méthode des solutions avec une fonction quelconque. C'est pourquoi il est important de connaître ces différentes méthodes.

ED : définitions de base

Ce cours aborde les équations différentielles homogènes, qui sont de la forme y'=ay, avec a non nul. Les solutions de ces équations sont de la forme k*exp(x), avec k une constante. Il y a une infinité de solutions pour cette équation. Cependant, en fixant une condition initiale, il n'y a qu'une seule fonction solution. La démonstration de ce résultat est présentée, en utilisant notamment une approche intuitive. Cette démonstration permet de trouver la forme générale des solutions, qui sont des exponentielles à x. La démonstration est ensuite développée de manière rigoureuse, en montrant que les solutions sont bien de la forme k*exp(x) et en vérifiant que cette forme satisfait bien l'équation différentielle.

Solutions Particulières

Les équations différentielles non homogènes se présentent sous la forme Y' = AY + F, où F est une fonction donnée. La solution à cette équation est la somme de deux termes : une solution homogène (Y' = AY) et une solution particulière (U' = AU + F). La solution homogène est déjà connue grâce au théorème précédent, et peut être écrite sous la forme k exp(AX), où k est une constante. La solution particulière, U, doit être trouvée en s'inspirant de la fonction F. Dans la plupart des cas, U sera de la même famille que F (par exemple, si F est une fonction affine, U sera de la forme AX + B). Dans les exercices plus complexes, on vous donnera des indications sur la famille à utiliser. Il est important de noter que la solution particulière n'est pas unique, mais l'ensemble des solutions sera de la forme U + V, où U est une solution particulière et V est une solution homogène. Il est également intéressant de noter que le cas des équations homogènes est inclus dans ce cas-ci, lorsque la fonction F est nulle. Dans ce cas, U sera égal à zéro. Trouver la solution particulière peut sembler complexe, mais en s'inspirant de la fonction F, on peut généralement trouver une solution de la même famille. Par exemple, si F est une fonction constante, la solution particulière sera également constante. Si F est une fonction quadratique, la solution particulière sera de la forme AX^2 + BX + C, où A, B et C sont des constantes à déterminer. Dans le cas où F est une constante, la solution particulière est simplement moins B sur 1. Il est important de maîtriser ce cas dans le programme. En conclusion, pour résoudre une équation différentielle non homogène, il faut trouver une solution homogène et une solution particulière, en s'inspirant de la fonction F. Avec ces deux termes, on obtient la solution générale de l'équation. En comprenant cette méthode, on peut résoudre la plupart des exercices de ce type. N'hésitez pas à poser des questions et à consulter l'FAQ pour plus de précisions.

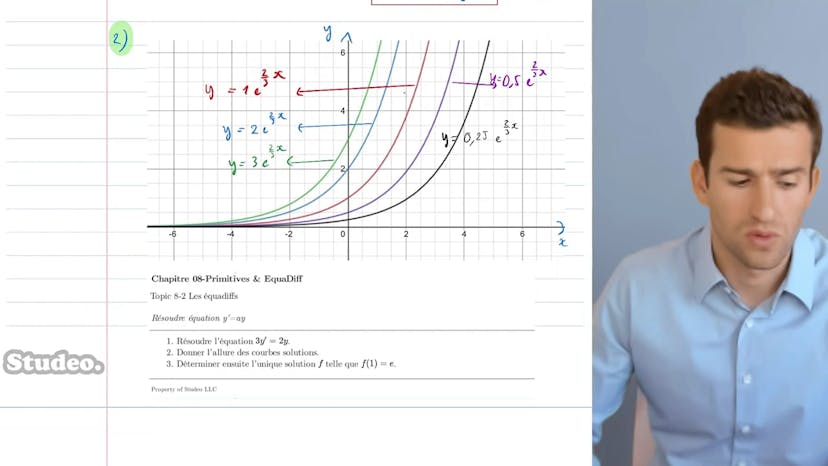
Équation y'=ay

Dans cette vidéo, nous allons apprendre à résoudre une équation différentielle de premier ordre à coefficient constant. Plus précisément, nous allons nous concentrer sur les équations du type y' = y, sans termes de second ordre, et avec des coefficients constants. Nous commençons par étudier l'équation différentielle donnée : 3y' = 2y. Nous divisons les deux côtés par 3 pour obtenir une forme du type y' = 2/3y. Ainsi, nous avons une équation de la forme y' = y, avec a égal à 2/3. En utilisant nos connaissances précédentes sur les équations de ce type, nous savons que les solutions sont de la forme k * e^(ax), où k est une constante réelle et e est la base du logarithme naturel. Dans notre cas, les solutions sont donc k * e^(2/3x), avec k appartenant à R réel. Ensuite, on nous demande de tracer les courbes représentant ces solutions. Ce qui varie ici, c'est la valeur de k, notre constante multiplicatrice. J'ai réalisé quelques exemples en prenant différentes valeurs pour k, allant de 0,25 à 3. Nous observons que plus k augmente, plus la courbe associée "décolle" et s'éloigne de l'axe des x. Il s'agit d'une exponentielle avec une constante multiplicatrice. Toutes ces courbes ont une allure similaire, appartenant à la même famille. Ensuite, on nous demande de déterminer parmi ces courbes celle qui vérifie f(1) = e. Dans les équations différentielles, lorsque nous avons une condition particulière, il existe une unique solution qui satisfait à la fois l'équation différentielle et cette condition particulière. Ici, nous voulons trouver la constante multiplicatrice k en utilisant la condition f(1) = e. Nous supposons que f(x) est de la forme de notre solution, c'est-à-dire k * e^(2/3x). Pour vérifier la condition en x = 1, nous remplaçons x par 1 et obtenons k * e^(2/3). Nous avons alors une simple équation en k que nous résolvons, ce qui donne k = e * e^(-2/3), soit e^(1/3). Ainsi, notre solution finale est f(x) = e^(1/3) * e^(2/3x). Ceci est une méthode très courante et classique pour résoudre une équation différentielle du type y' = y avec une condition initiale. Si vous avez des questions supplémentaires, veuillez consulter la FAQ.

Équation y'=ay+b

Aujourd'hui, nous allons nous intéresser à la résolution des équations différentielles du premier ordre avec un second membre, c'est-à-dire les équations de la forme y' = y + b. La méthode est assez simple : nous commençons par chercher une solution constante, que nous appelons la solution particulière. Ensuite, nous résolvons l'équation homogène, qui est y' = y. Enfin, nous combinons ces deux solutions pour obtenir la solution générale. Prenons l'exemple de l'équation y' = -y + 3, où a = -1 et b = 3. Nous résolvons d'abord l'équation homogène y' = -y, dont les solutions sont de la forme y(x) = ae^(-x), où a est une constante réelle. Ensuite, nous recherchons une solution particulière constante, en supposant que sa dérivée est nulle. En injectant cette solution dans l'équation, nous trouvons que phi = 3. Enfin, nous combinons ces deux solutions pour obtenir la forme générale de la solution y(x) = e^(-x) + 3a, où a est une constante multiplicative inconnue. Il est important de noter qu'il y a toujours une constante multiplicative dans la solution générale. Parfois, pour déterminer sa valeur, nous avons besoin d'une condition particulière, par exemple y(alpha) = beta. Dans ce cas, il y aura une unique solution qui vérifiera cette condition particulière. Voilà comment résoudre une équation différentielle du premier ordre de la forme y' = y + b. N'hésitez pas à poser vos questions dans la description.

Équation y'=ay+φ

La différence entre b et phi dans l'équation différentielle y' = y + phi est que b est une constante tandis que phi est une fonction qui peut varier. La méthode pour résoudre cette équation est la même que pour l'équation y' = y + b. On cherche d'abord une solution particulière en résolvant l'équation sans l'équation homogène, c'est-à-dire en résolvant y' = y. Ensuite, on trouve la solution particulière en utilisant un indice donné dans l'énoncé. Dans l'énoncé, on nous demande de vérifier si la fonction p(x) est une solution de l'équation p'(x) = x^2 + 2x - 1. Pour cela, on prend p(x) comme un polynôme et on calcule sa dérivée. Ensuite, on vérifie si 2p'(x) + 6p(x) = x^2 + 2x - 1. Si c'est le cas, on conclut que p(x) est une solution de l'équation. Ensuite, on nous demande de montrer que si f(x) est une solution de l'équation y' = y + phi, alors f(x) - p(x) est une solution de l'équation y' = y. Pour cela, on remplace phi par p(x) dans l'équation y' = y + phi, ce qui nous donne 2f'(x) - 2p'(x) + 6f(x) - 6p(x) = 0. En factorisant, on obtient 2(f(x) - p(x)) - 2p'(x) + 6(f(x) - p(x)) - 6p(x) = 0. On reconnaît alors l'équation y' = y et on conclut que f(x) - p(x) est une solution de cette équation. Grâce à cette équivalence, on peut en déduire les solutions de l'équation y' = y + phi en résolvant l'équation y' = y. On trouve que les solutions sont de la forme f(x) - p(x), où f(x) - p(x) = A * e^(-3x) et A est un réel. Il est important de noter qu'il y a toujours une constante multiplicative inconnue dans les solutions des équations différentielles de ce type. Pour la trouver, on a besoin de conditions particulières qui ne sont pas données dans cet exemple.

Second membre en exponentielle

Les équations différentielles sont un concept essentiel en ingénierie. Pour résoudre une équation du premier ordre du type Y' + Ay = Φ(X), la solution se compose de deux parties. La première partie est la solution générale sans second membre, c'est-à-dire la solution de Y' + Ay = 0, en général un terme exponentiel. La deuxième partie est une solution particulière qui vérifie l'équation avec Φ(X). Pour trouver cette solution particulière, on observe la nature de Φ(X) et on tente une fonction qui lui ressemble. Cela fonctionne dans la plupart des cas, sinon il faut complexifier la fonction. Si Φ(X) est une somme de termes, on peut séparer l'équation en problèmes distincts. En résolvant l'équation donnée, avec Φ(X) = e^(2X), on trouve une solution particulière qui est 1/5 * e^(2X). La solution générale est donc Y = K * e^(2X) + 1/5 * e^(2X), où K est une constante réelle. En fixant Y(0) = 1, on trouve K = 4/5, donc la solution finale est Y = (8/5) * e^(2X) + (1/5) * e^(2X).

Solution particulière : trigonométrie

Dans ce cours, nous abordons l'équation différentielle. Nous recherchons une solution particulière en utilisant la forme donnée dans l'énoncé. En essayant A fois cos x, nous remarquons que cela ne fonctionne pas car il y a du sin dans l'équation. La meilleure technique consiste à utiliser à la fois cos et sin pour obtenir une solution. Nous identifions les termes en cos et en sin dans l'équation et obtenons 0 sin, moins un cinquième cos x et plus deux cinquièmes sin x. En utilisant cette information, nous réécrivons l'équation sous une forme plus simple, y prime moins 1 demi de y égale 1 demi de cos x. En résolvant l'équation, nous obtenons la solution générique y de x égale exponentielle de 1 demi de x fois grand K plus g de x, où g de x représente la solution sans second membre. Finalement, nous obtenons la fonction générale en faisant la somme de la solution particulière et de la solution sans second membre.

Solution particulière plus difficile

Dans ce cours, nous étudions une équation différentielle de la forme y'-2y = xe2x. Pour résoudre cette équation, nous cherchons une solution particulière. En identifiant la structure de cette équation, nous essayons d'abord avec ax+b. Cependant, nous remarquons que cela ne fonctionne pas car la structure de cette solution ne correspond pas à notre équation. Nous en déduisons qu'il faut augmenter le degré de la solution. Nous tentons ensuite avec g2x = ax²+bx+c. Après quelques calculs, nous constatons que les termes x² s'annulent, ce qui nous permet de trouver une solution. La solution générale est donnée par y2x = ke2x + g2x, où k est une constante réelle et g2x = 1/2 x² e2x. Cela signifie que toutes les solutions de cette équation peuvent être exprimées de cette manière, en variant la valeur de k en fonction des conditions initiales.

Ordre 1 coeffs constants

Aucun résumé n'est disponible pour cette vidéo

Variation de la constante

Dans cette vidéo, Maty de studio aborde la résolution d'équations différentielles linéaires d'ordre 1 en utilisant la méthode de la variation de la constante. Il commence par résoudre l'équation y'y = 1/(1 + exp(x)) en trouvant la solution homogène, qui est yh = x * exp(-x). Pour trouver une solution particulière, il utilise la méthode de la variation de la constante en posant la solution cherchée comme y = A(x) * exp(-x), où A(x) est une fonction de x. Après des calculs, il obtient la solution particulière yp = ln(1 + exp(x)) * exp(-x). Il rappelle ensuite qu'il faut ajouter la solution homogène à la solution particulière pour obtenir l'ensemble des solutions de l'équation, qui est l'ensemble des fonctions de la forme y = exp(-x) * (c + ln(1 + exp(x))), où c est un réel. Maty poursuit avec d'autres équations différentielles linéaires d'ordre 1, en utilisant la même méthode de la variation de la constante. Il donne les étapes de résolution pour chaque équation et obtient les solutions correspondantes. Il termine en soulignant l'importance de la méthode de la variation de la constante, qui permet de résoudre toutes les équations différentielles d'ordre 1, sauf dans certains cas où il faut utiliser d'autres méthodes. Il rappelle également de bien multiplier la solution particulière par le facteur exponentiel et de toujours ajouter la solution homogène.

Avec condition initiale

Dans cette vidéo sur la résolution des problèmes de Cauchy, Mathis explique qu'un problème de Cauchy correspond à la fois à une équation différentielle et à des conditions initiales pour la fonction en question. Il résout ensuite deux équations différentielles. Pour la première équation, y' + tan(t)y = sin(t), avec y(0) = 1, Mathis commence par trouver les solutions homogènes, c'est-à-dire les solutions de y' + tan(t)y = 0. Il utilise une technique de variation de la constante et trouve que les solutions homogènes sont de la forme a*cos(t), où a est un nombre réel quelconque. Ensuite, Mathis cherche une solution particulière de l'équation complète. Il pose ys = a(t)*cos(t), où a(t) est une fonction de t. En dérivant ys et en remplaçant dans l'équation, il trouve que a'(t) = -2*sin(t). En intégrant a'(t), il obtient a(t) = 2*cos(t) + c, où c est une constante. Maintenant, Mathis somme la solution homogène et la solution particulière en tenant compte de la condition initiale y(0) = 1. Il trouve que a doit être égal à -3, ce qui donne la solution unique y(t) = 3*cos(t) - 2*cos^2(t). Pour la deuxième équation, x*y' + xy = x^2 - x + 1, avec y(1) = 1, Mathis commence par trouver la solution homogène, qui est y' + x/(1+x)*y = 0. Il utilise une technique de variation de la constante et trouve que les solutions homogènes sont de la forme (x+1)^(-x)*e^a*x, où a est un nombre réel quelconque. Ensuite, Mathis cherche une solution particulière de l'équation complète. Il pose ys = (x+1)*(ax+b), où a et b sont de constantes. En remplaçant ys dans l'équation, il trouve que a = 1 et b = -2. Maintenant, Mathis somme la solution homogène et la solution particulière en tenant compte de la condition initiale y(1) = 1. Il trouve que a doit être égal à e^1, ce qui donne la solution unique y(x) = (x+1)*e^(1-x) + x - 2. En conclusion, Mathis rappelle qu'il faut bien sommer les solutions homogènes et particulières avant d'appliquer les conditions initiales, et que cela donne une unique solution pour chaque problème de Cauchy.

Gérer une valeur absolue

Dans cette vidéo, nous résolvons une équation différentielle sur deux intervalles différents : moins l'infini à 0 et 0 à plus l'infini. L'équation est de la forme |x*y'| + (x-1)y = x^3. Sur l'intervalle moins l'infini à 0, nous décomposons l'expression en utilisant la valeur absolue de x, qui est égale à -x. Nous simplifions ainsi l'équation pour obtenir y' + (1-x/x)y = -x^2. En résolvant cette équation homogène, nous trouvons que la solution homogène est y = Ae^x/x, où A est une constante réelle. Ensuite, nous cherchons une solution particulière en utilisant la méthode de variation de la constante. En intégrant l'expression x^3e^(-x), nous trouvons que la solution particulière est y = (x^2 + 3x + 6 + 6/x)e^x/x. Ainsi, l'ensemble des solutions sur l'intervalle moins l'infini à 0 est l'ensemble des fonctions de la forme y = (Ae^x/x) + (x^2 + 3x + 6 + 6/x)e^x/x, où A est une constante réelle. Sur l'intervalle 0 à plus l'infini, l'équation différentielle est différente : y' + (x-1/x)y = x^2. La solution homogène est y = Axe^(-x), où A est une constante réelle. En utilisant la variation de la constante, nous trouvons que la solution particulière est y = (x-1)e^x * x. Ainsi, l'ensemble des solutions sur l'intervalle 0 à plus l'infini est l'ensemble des fonctions de la forme y = Axe^(-x) + (x-1)e^x * x, où A est une constante réelle. En conclusion, il est important de faire attention aux intervalles de résolution demandés, car cela peut influencer les solutions de l'équation différentielle.

Changement de variable

Dans cette vidéo, Mathis de studio résout une équation différentielle en utilisant un changement d'inconnu. L'équation différentielle E1 est de la forme -x^2z' + xz = z^2. L'objectif est de trouver les solutions de E1 sur l'intervalle [1, +∞] qui ne s'annulent pas sur [1, +∞]. Puisqu'E1 n'est pas linéaire en raison de la puissance 2 de z, Mathis introduit une nouvelle variable y égale à 1/z pour linéariser l'équation. En remplaçant z par 1/y, l'équation devient -x^2(1/y)' + x/y = 1/y^2. Grâce à ce changement d'inconnu, Mathis obtient une équation différentielle linéaire du premier ordre, notée E2, qui est y' + (1/xy) = 1/x^2. Pour résoudre E2, Mathis utilise la méthode classique de séparation de variables. Il trouve la solution homogène y_h(x) = a/x, où a est une constante. Pour la solution particulière, Mathis utilise la méthode de la variation de la constante en posant y_p(x) = u(x)/x. En dérivant y_p(x), il obtient u'(x)/x - u(x)/x^2 = 1/x^2, ce qui donne u'(x)/x = 1/x. En intégrant de part et d'autre, Mathis obtient u(x) = ln|x|. Ainsi, la solution particulière est y_p(x) = ln|x|/x. La solution générale de E2 est donc y(x) = y_h(x) + y_p(x) = a/x + ln|x|/x. Pour trouver les solutions de E1 sur [1, +∞] qui ne s'annulent pas sur [1, +∞], on doit prendre l'inverse de y(x) en s'assurant que le dénominateur ne s'annule pas. Donc, les solutions de E1 sur [1, +∞] qui ne s'annulent pas sur cet intervalle sont y(x) = (a + ln|x|)/x, où a est un nombre réel positif. Mathis conclut en soulignant l'utilité d'un changement d'inconnu pour résoudre une équation différentielle qui ne peut pas être résolue par des méthodes classiques. Il encourage les spectateurs à utiliser cette méthode pour aller au-delà de ce qu'ils ont appris. Il termine en remerciant les spectateurs et en leur donnant rendez-vous pour la prochaine vidéo.