Cours de Espaces vectoriel dimension finie et Applications linéaires en Ligne par les Meilleurs Professeurs - Espaces vectoriel dimension finie et Applications linéaires

Base

Ce cours porte sur la discussion de différentes familles de vecteurs pour déterminer si elles peuvent être des bases de l'espace R3 (espace à trois dimensions). Le professeur examine plusieurs familles de vecteurs et utilise les concepts de liberté et de génération pour les évaluer. Une base est à la fois libre (aucune combinaison linéaire ne peut donner le vecteur nul, sauf si tous les coefficients sont nuls) et génératrice (tous les vecteurs de l'espace peuvent être obtenus par des combinaisons linéaires des vecteurs de la famille). Deux des familles sont rapidement éliminées car elles ne contiennent pas le bon nombre d'éléments pour former une base. Les deux familles restantes sont étudiées plus en détail. Le professeur utilise des tests de liberté (vérification qu'aucune combinaison linéaire ne donne le vecteur nul, sauf si les coefficients sont nuls) pour discuter de différents cas. Il fait des combinaisons linéaires des vecteurs et utilise des méthodes d'élimination gaussienne pour résoudre les systèmes d'équations. Le professeur conclut que l'une des familles est une base lorsque certaines conditions sont remplies, tandis que l'autre famille ne peut pas être une base car elle ne génère pas tous les vecteurs de l'espace. En résumé, le cours analyse différentes familles de vecteurs pour déterminer si elles peuvent être des bases de l'espace R3, en utilisant des tests de liberté et des méthodes d'élimination gaussienne pour résoudre les systèmes d'équations. Deux familles sont éliminées en raison du nombre incorrect d'éléments, tandis que les deux familles restantes sont discutées en détail pour déterminer leur statut de base.

Coordonnées de polynômes

Dans cette vidéo, on étudie les espaces de polynômes. L'objectif est de montrer que les polynômes P1, P2 et P3 forment une base de R²x, qui est l'ensemble des polynômes du degré 2 dans R. Pour cela, on utilise la méthode de se référer à une base connue, en l'occurrence vec(1, x, x2). On utilise deux identités remarquables, x+1 et x-1, pour montrer que vec(P1, P2, P3) est égal à vec(1, x, x2). En faisant des combinaisons linéaires, on trouve que vec(P1, P2, P3) est égal à vec(P1 + P3 - 2P2). Pour obtenir un vecteur constant, on enlève exprès -2P2. En fin de compte, on obtient que P3 - P1 est égal à 2x2 + 4x, ce qui est bien un vecteur de 1x2 x1, 1x2. Les coordonnées de ce vecteur dans la base P1, P2, P3 sont donc un quart de P1 + trois quarts de P3.

Dimension

Dans ce cours, nous étudions un exercice basé sur des jeux de combinaisons linéaires. Nous avons cinq vecteurs de R4 (un espace de dimension 4). Nous les divisons en deux groupes : les trois premiers vecteurs dans le groupe F et les deux derniers vecteurs dans le groupe G. Nous utilisons les combinaisons linéaires pour déterminer la dimension de F. En recombinant les vecteurs, nous trouvons que f (qui est la combinaison linéaire de V1, V2 et V3) a une dimension de 3. Ensuite, nous examinons G et constatons que V4 et V5 ne sont pas colinéaires, donc la dimension de G est de 2. Nous essayons de voir si nous pouvons trouver une base de R4 en ajoutant V4 à F ou en l'ajoutant négativement. Nous constatons que V4 ne peut pas être représenté comme une combinaison linéaire de V1, V2 et V3, ce qui signifie que F et V4 forment une famille libre et une base de R4. Nous concluons que F plus G égale R4, car nous avons une base pour R4. Enfin, nous calculons la dimension de F inter G. Utilisant la formule liant les dimensions de ces deux espaces, nous trouvons que F inter G a une dimension de 1. En résumé, la dimension de F plus G est de 4, la dimension de F inter G est de 1. Nous utilisons des techniques de combinaisons linéaires pour obtenir ces résultats.

Base d’espace de polynômes

Dans cette transcription de vidéo, il est question de démontrer qu'une famille de polynômes dans l'espace des polynômes de degré n forme une base si les degrés des polynômes sont échelonnés. C'est un théorème courant et facile à démontrer. L'auteur mentionne qu'il a utilisé ce théorème lors d'un exercice oral pour résoudre l'exercice plus rapidement. Il explique également comment écrire un polynôme dans une certaine forme en utilisant des polynômes avec des degrés échelonnés. L'auteur donne des détails étape par étape pour effectuer cette transformation. Il conclut en rappelant l'importance de connaître ce théorème et souhaite retrouver le public dans une prochaine vidéo.

Noyau et image

Dans cet exercice, nous étudions les applications linéaires dans l'espace des polynômes de degré n. Il est important de noter que cet espace a une dimension de n+1, contrairement à ce que l'on pourrait croire. La base de cet espace est composée des polynômes de degré n, n-1, 1 et 0. Dans cet exercice, nous avons une application linéaire définie par phi(p) = p(x+1) - p(x). Pour vérifier que c'est un endomorphisme, il faut montrer que c'est linéaire et que l'image de phi est incluse dans E. Pour la linéarité, on peut simplement le mentionner car c'est évident puisque tout est défini avec des signes moins. Pour montrer que l'image de phi est incluse dans E, on calcule phi(xi) et on utilise le binôme de Newton. On trouve que l'image de phi est incluse dans l'ensemble des polynômes de degré n-1. Ensuite, on s'intéresse à l'égalité de phi au carré, c'est-à-dire phi². On remarque que l'image de phi n'est pas égale à l'espace E, mais elle est incluse dans E. Les polynômes de degré n ne sont jamais atteints par phi. Il est important de ne pas commencer par résoudre phi², mais plutôt d'étudier l'image de phi, car cela peut simplifier les choses. On utilise le théorème de Durand, qui dit que la dimension de l'image de phi plus la dimension du noyau de phi équivaut à la dimension de l'espace de départ. Dans notre cas, la dimension de l'image de phi est n-1 et la dimension de l'espace de départ est n+1. Donc la dimension du noyau de phi est de 1. En utilisant l'astuce que si deux espaces ont la même dimension et que l'un est inclus dans l'autre, alors ils sont égaux, on peut conclure que le noyau de phi est égal à l'espace E. En résumé, dans cet exercice, nous avons étudié une application linéaire dans l'espace des polynômes de degré n. Nous avons montré qu'elle est linéaire et que son image est incluse dans l'ensemble des polynômes de degré n-1. De plus, nous avons utilisé le théorème de Durand et l'astuce de la dimension pour montrer que le noyau de l'application est égal à l'espace E.

Théorème du rang

Dans cet exercice, on considère un espace vectoriel E de dimension finie et deux endomorphismes F et G qui vérifient les équations E = kref + krg et E = imef + img. L'objectif est de montrer que les sommes sont directes, c'est-à-dire qu'il n'y a aucun élément commun à part 0. Pour résoudre cet exercice, on utilise le théorème du rang qui nous donne des expressions pour la dimension de E en fonction du rang de F et G ainsi que de la dimension de leurs noyaux respectifs. On utilise également la formule pour la dimension d'une somme d'espaces. En appliquant ces formules, on obtient deux équations donnant le rang de F plus le rang de G. En combinant ces équations, on montre que le rang de F plus le rang de G est égal à la dimension de E. Cela implique que la dimension de l'intersection des noyaux est nulle, ce qui prouve que les sommes sont directes. Cet exercice nécessite de bien connaître les formules du théorème du rang et de la dimension d'une somme d'espaces. Il est conseillé de poser les formules et de faire des calculs intermédiaires pour vérifier les résultats.

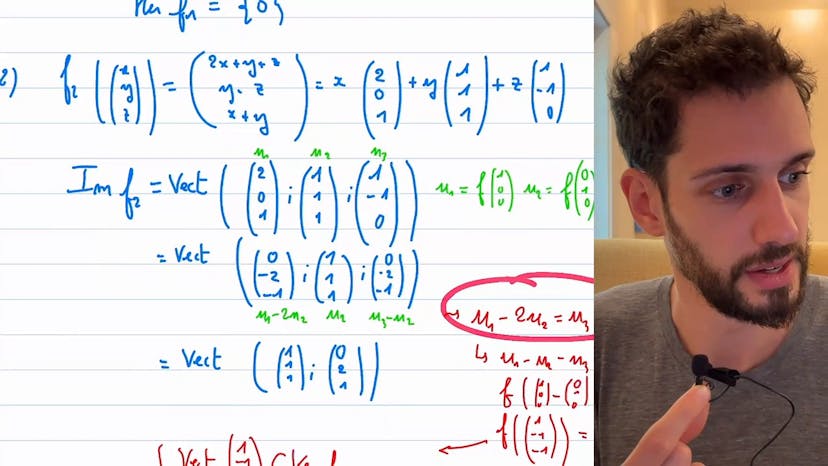
Injectivité et surjectivité

Dans cet exercice, nous étudions des applications linéaires avec des exemples concrets d'applications linéaires et nous déterminons les noyaux et les images de ces applications. Nous examinons chaque application pour déterminer si elle est injective, bijective ou surjective. En dimension finie, être injective, surjective ou bijective est complètement équivalent. Être injective signifie que le noyau est réduit à zéro. Être surjective signifie que l'image est égale à l'espace d'arrivée. Être bijective signifie que les deux sont vrais. En dimension infinie, cela peut être différent. Pour chaque fonction, nous analysons si elle est endomorphisme en restant dans R2 ou R3. Si les espaces de départ et d'arrivée sont différents ou si les dimensions sont différentes, cela ne sera pas un endomorphisme. En utilisant la technique de rédaction en colonne, nous pouvons déterminer l'image de chaque fonction. Nous utilisons des combinaisons linéaires pour trouver des vecteurs indépendants qui composent l'image. Nous utilisons également ces combinaisons linéaires pour trouver les vecteurs du noyau en utilisant une équation de la forme f(x) = 0. En comprenant les relations entre les vecteurs dans l'espace d'arrivée, nous pouvons déterminer les éléments du noyau.

Forme linéaire

Dans ce cours, nous étudions les formes linéaires, qui sont des applications linéaires avec un espace d'arrivée égal au corps de base. Nous devons montrer que toute forme linéaire non nulle est surjective. En d'autres termes, il faut montrer que pour chaque élément dans l'espace de départ, il existe au moins un élément correspondant dans l'espace d'arrivée. Nous commençons par noter que l'image de la forme linéaire est incluse dans le corps de base. Puisque l'espace d'arrivée est petit, cela indique que le rang de la forme linéaire est inférieur ou égal à 1. Si le rang est égal à 0, cela signifie que la forme linéaire envoie tous les éléments sur 0, ce qui est l'application nulle, mais ce n'est pas le cas ici. Donc, le rang de la forme linéaire est égal à 1, ce qui nous permet de conclure que l'image de la forme linéaire est égale au corps de base, ce qui signifie que la fonction est surjective. Ensuite, nous déduisons que le noyau d'une forme linéaire non nulle est un sous-espace vectoriel de dimension n-1. Cela est dû au théorème du rang, qui stipule que la somme des dimensions du noyau et de l'image est égale à la dimension de l'espace de départ. Par conséquent, la dimension du noyau est égale à la dimension de l'image, soit n-1. Ensuite, nous nous intéressons à la réciproque. Nous prenons un sous-espace vectoriel H de dimension n-1 et vérifions s'il est possible de trouver une forme linéaire dont le noyau est H. Pour simplifier les choses, nous donnons une base à H, composée de n-1 vecteurs indépendants. En utilisant le théorème de la base incomplète, nous pouvons compléter H en ajoutant un élément U qui n'est pas dans H, de sorte que l'union de H et de U forme une base de l'espace de départ E. Ainsi, tout élément X de E peut être écrit comme une combinaison linéaire des vecteurs de H, plus une combinaison linéaire de U. Ensuite, pour trouver une forme linéaire intéressante, nous définissons phi comme l'application qui prend un élément X de E et qui donne simplement sa coordonnée Xn sur le vecteur U. Cela signifie que tout élément de H sera envoyé sur 0. En résumé, pour un élément X appartenant à H, nous avons phi(X) = 0. Enfin, nous montrons que si d'autres formes linéaires ont H comme noyau, elles seront parallèles à celle décrite précédemment, c'est-à-dire qu'elles seront de la forme lambda fois cette forme linéaire. Pour le prouver, nous utilisons à nouveau la décomposition de l'espace E en combinaison linéaire des vecteurs de H et de U. En appliquant une autre forme linéaire phi à un grand X exprimé de cette manière, nous pouvons séparer les termes correspondants à H et à U. Puisque les éléments correspondants à H sont dans le noyau de phi, leur image sera toujours égale à 0. Ensuite, nous remarquons que phi(U) est égal à lambda fois phi(X), où lambda est une constante. Ainsi, nous concluons que toute autre forme linéaire avec H comme noyau sera de la forme lambda phi(X).