 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc
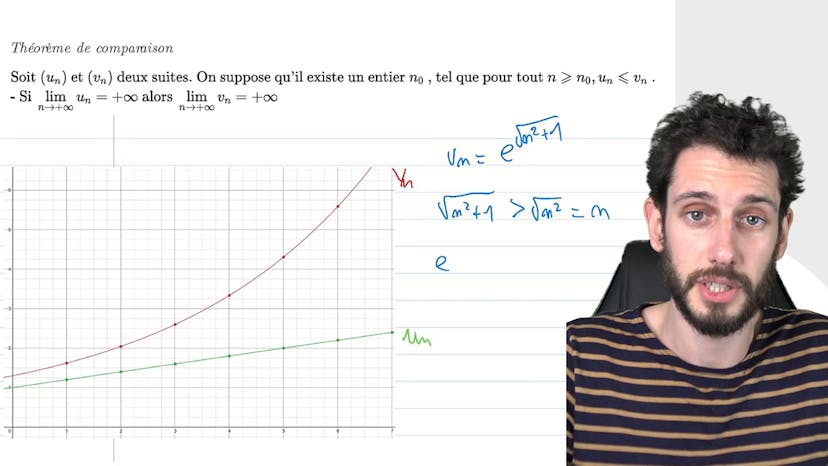
Théorème de comparaison - illustration
Le théorème de comparaison en mathématiques est un outil puissant qui permet d'économiser beaucoup d'efforts lors des démonstrations. Il consiste à comparer une suite complexe Vn à une suite plus simple Un, et si Un tend vers l'infini, alors Vn tendra également vers l'infini. Cela permet d'éviter de devoir manipuler des expressions compliquées et de résoudre des problèmes complexes. Par exemple, si on a la suite Vn définie comme l'exponentielle de la racine de n² plus 1, qui est difficile à gérer, on peut trouver une suite Un plus simple, comme la suite racine de n², et comparer les deux. En utilisant le fait que l'exponentielle est une fonction croissante, on peut conclure que Vn sera plus grand que Un, et donc Vn tendra vers l'infini. Ainsi, on évite de devoir étudier en détail la suite Vn et de faire de nombreuses manipulations complexes. C'est la beauté du théorème de comparaison en mathématiques.
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème des gendarmes
Le théorème de comparaison permet de démontrer que, si une suite VN tend vers l'infini, en la comparant à une suite UN plus petite et plus simple. Le théorème d'encadrement, également appelé théorème des gendarmes, est l'équivalent pour une limite finie. Il permet de montrer qu'une suite tend vers un réel fini en étant "prisonnière" entre deux autres suites convergentes vers la même limite. Ce théorème est très utile pour obtenir des résultats sur les suites sans avoir à se soucier des définitions formelles d'ε et d'A.
Pour illustrer ce théorème, on prend l'exemple de la fonction sinus, qui converge vers 0. On encadre la suite sinn/n entre -1/n et 1/n, qui convergent toutes les deux vers 0. En utilisant le théorème des gendarmes, on peut en déduire que la suite sinn/n converge également vers 0. Ce théorème permet donc de simplifier les calculs en encadrant des suites plus complexes entre des suites plus simples dont on connaît la limite.
Cependant, il n'est pas toujours possible d'utiliser le théorème des gendarmes dans toutes les situations. Parfois, on dispose de moins d'informations et on peut donc affirmer moins de choses. Néanmoins, il existe d'autres propriétés des suites, comme le fait que si deux suites sont ordonnées et convergentes, alors leurs limites seront également ordonnées de la même manière. Cette propriété intuitive doit également être connue et comprise.
En résumé, le théorème des gendarmes, ou théorème d'encadrement, permet de démontrer que si une suite est "coincée" entre deux autres suites convergentes vers la même limite, alors elle converge également vers cette limite. Ce théorème est très pratique pour simplifier les calculs et obtenir des résultats sur les suites.
Maths SM&SP
Analyse
2BAC SM Maroc

Définitions + th de CV monotone
Une suite est dite majorée lorsqu'elle ne dépasse pas une certaine valeur. Elle peut avoir plusieurs majorants, c'est-à-dire plusieurs valeurs qui la bloquent par le haut. Une suite est minorée lorsqu'elle ne descend pas en dessous d'une certaine valeur. De même, elle peut avoir plusieurs minorants, c'est-à-dire plusieurs valeurs qui la bloquent par le bas. Lorsqu'une suite est à la fois majorée et minorée, on dit qu'elle est bornée.
Le théorème de convergence monotone établit que si une suite est croissante et majorée, alors elle converge. De même, si une suite est décroissante et minorée, elle converge également. Si une suite croissante n'est pas majorée, elle tend vers plus l'infini, tandis qu'une suite décroissante non minorée tend vers moins l'infini.
Il est important de noter que la réciproque du théorème de convergence monotone est fausse. Une suite peut converger sans être croissante ou décroissante. Par exemple, la suite sinus(1/n) converge vers 0, bien qu'elle oscille de manière irrégulière.
Il est essentiel de bien comprendre ces concepts pour éviter de se tromper dans les exercices et les questions de cours.
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème de comparaison - Illustration
Le théorème de comparaison est un outil puissant en mathématiques qui permet d'éviter de nombreuses démonstrations fastidieuses. En bref, si une suite Vn peut être comparée à une suite plus simple, et que cette dernière tend vers l'infini, alors on peut conclure que Vn tend également vers l'infini. Ce théorème est pratique car il permet de traiter des suites compliquées et de les comparer à des suites plus faciles à étudier. Par exemple, si on souhaite démontrer que la suite Vn = exp(n² + 1) tend vers l'infini, on peut la comparer à la suite Un = exp(n), qui est simple et diverge vers l'infini. En utilisant le fait que l'exponentielle est une fonction croissante, on peut conclure que Vn sera plus grand que Un, et donc tendra également vers l'infini. Ainsi, grâce au théorème de comparaison, on peut faire des économies d'efforts en évitant de faire des démonstrations détaillées. Dans la prochaine vidéo, nous verrons la démonstration de ce théorème.
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème de comparaison - démonstration
Le cours explique comment démontrer le théorème de divergence en mathématiques, en utilisant une approche SEO-friendly. Le professeur commence par expliquer que malgré l'avantage de ce théorème de se passer des démonstrations en epsilon et en grand A, il est nécessaire de revenir à la définition pour la démontrer. Le professeur démontre ensuite que si la limite d'une suite tend vers l'infini, alors il existe un certain rang à partir duquel tous les éléments de cette suite sont plus grands qu'un certain nombre A positif. En utilisant cette information, le professeur conclut que pour tout A positif, il existe un certain rang à partir duquel tous les éléments de la suite sont plus grands que A. Finalement, le professeur résume cette démonstration en expliquant que pour tout A positif, il existe un certain rang à partir duquel tous les éléments de la suite sont plus grands que A, ce qui correspond à la définition de la divergence vers l'infini. En utilisant cette démonstration, il n'est plus nécessaire d'utiliser des démonstrations plus complexes avec des grands A et des petits epsilon.
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème des gendarmes
Le théorème d'encadrement, aussi appelé le théorème des gendarmes, est l'équivalent du théorème de comparaison pour les limites finies. Il permet de démontrer que si une suite est "encadrée" entre deux autres suites convergentes vers la même limite, alors cette suite sera également convergente vers cette même limite.
Pour illustrer ce concept, prenons l'exemple de la suite sinus n sur n. Cette suite est un peu complexe à analyser directement, mais nous pouvons l'encadrer en utilisant les fonctions sinx sur x et les suites 1 sur n et -1 sur n, qui convergent toutes deux vers 0. En utilisant le théorème des gendarmes, nous pouvons donc conclure que la suite sinus n sur n converge également vers 0.
Il est important de noter que le théorème des gendarmes n'est pas toujours applicable et que parfois nous avons moins d'informations pour pouvoir déduire autant. Cependant, une propriété importante à retenir est que si deux suites un et vn sont ordonnées, c'est-à-dire que un est toujours plus petit que vn, et que ces deux suites convergent, alors leurs limites seront également ordonnées de la même manière, la limite de un étant plus petite que la limite de vn.
N'hésitez pas à poser des questions et à discuter avec d'autres étudiants pour clarifier des points.
Maths SM&SP
Analyse
2BAC SM Maroc
Suites majorées, minorées & le th de convergence monotone
Aucun résumé n'est disponible pour cette vidéo
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème des gendarmes
Le théorème d'encadrement, également connu sous le nom de théorème des gendarmes, permet de montrer que si une suite est prise en sandwich entre deux autres suites qui convergent vers la même limite finie, alors elle converge également vers cette limite. Ce théorème peut être utilisé pour démontrer des résultats sur les suites sans avoir à s'embêter avec les définitions formelles.
Dans l'exemple donné, la fonction sin(x) est tracée et semble converger vers 0. Cependant, la suite sin(n)/n est plus difficile à gérer. Pour simplifier, on peut encadrer sin(x)/x entre -1/x et 1/x. En traçant les deux fonctions, on constate qu'elles encadrent parfaitement la suite sin(n)/n. On sait que les suites 1/n et -1/n convergent vers 0, donc on peut conclure que la suite sin(n)/n converge également vers 0.
Il est important de noter que même si le théorème des gendarmes peut être très pratique, il ne s'applique pas toujours et il est possible de dire moins de choses dans certaines situations. Cependant, une propriété importante à retenir est que si deux suites sont ordonnées (un toujours plus petit que vn) et qu'elles convergent, alors leurs limites respectives seront également ordonnées (la limite de vn sera plus petite que la limite de vn).
Maths SM&SP
Analyse
2BAC SM Maroc

Suite majorée, minorée & Th de convergence monotone
Le cours aborde les définitions des concepts de majoration, minoration et bornitude pour les suites. On dit qu'une suite est majorée lorsque ses termes sont tous bloqués par une certaine valeur, et on dit qu'une suite est minorée lorsque ses valeurs ne peuvent pas descendre en dessous d'une certaine valeur. Une suite bornée est à la fois majorée et minorée.
L'exemple d'une suite croissante 2-1/n est donné, montrant qu'elle est majorée par 2. D'autres exemples de suites majorées, minorées et bornées sont également donnés, montrant différentes variations de comportement.
Le théorème de convergence monotone est introduit, qui établit une relation entre la croissance et la majoration d'une suite. Si une suite est croissante et majorée, alors elle converge. Cependant, il est souligné que ce théorème ne donne pas accès à la valeur limite de la suite. Il est nécessaire de faire une étude plus approfondie pour trouver la limite.
Le cours aborde également les cas où une suite peut converger vers l'infini positif ou négatif, même si elle n'est pas croissante ou décroissante. Des exemples de suites qui tendent vers l'infini positif ou négatif sont donnés, illustrant que la réciproque du théorème de convergence monotone est fausse.
En conclusion, il est souligné l'importance de ne pas se laisser piéger par de fausses idées sur la convergence des suites, et il est encouragé à poser des questions et à participer aux discussions avec les autres étudiants.
Maths SM&SP
Analyse
2BAC SM Maroc

Th convergence monotone - démo
Le théorème de convergence monotone démontre que dans le cas d'une suite croissante non majorée, c'est-à-dire une suite qui n'est jamais bloquée, celle-ci tend vers l'infini. On va revenir à la définition formelle de la convergence vers l'infini et on va réaliser que c'est quasiment la même chose que cette définition formelle, donc la démonstration ne sera pas compliquée.
On commence par fixer un A positif strict. L'objectif sera de montrer qu'il existe un rang à partir duquel tous les termes de la suite sont supérieurs à A. Ce qui signifie que tout A finira par être dépassé. Comme la suite UN n'est pas majorée, il existera donc un rang P tel qu'à partir de ce rang, UP sera plus grand que A.
En combinant cela avec le fait que la suite est croissante, on peut affirmer que pour tout N supérieur à P, UN sera toujours plus grand que UP. Cela signifie donc qu'à partir de P, pour tout N supérieur à P, UN sera strictement supérieur à A.
Ainsi, on a démontré que pour tout A fixé, il existe un rang à partir duquel tous les termes de la suite sont supérieurs à A. Cela confirme donc la convergence vers l'infini. Deux conclusions sont à retenir : la suite finit toujours par être au-dessus de tout A fixé et cela explique le concept de tendance vers l'infini.
C'est tout pour cette démonstration, à la prochaine.
Maths SM&SP
Analyse
2BAC SM Maroc

Encadrer sin(n)
Dans ce cours, nous étudions les fonctions sinus et moins 1 plus sin dans le contexte des théorèmes de convergence. Nous examinons la suite un = n + 2*sin(n) et montrons que pour tout n, un est supérieur à n-2.
Pour cela, nous utilisons l'encadrement du sinus entre -1 et 1 pour obtenir un encadrement de un. Puisque le sinus n'a pas de limite définie, il est essentiel de l'encadrer. En multipliant le sinus par 2 (ce qui est positif) et en ajoutant n, nous obtenons un qui est supérieur à n-2. Bien que cette partie de l'inéquation ne soit pas notre objectif, elle est néanmoins vraie.
En effet, un est compris entre n-2 et n+2. Nous nous intéressons principalement à la première partie de cette inéquation. Puisque n-2 tend vers l'infini et que un est supérieur à une suite qui tend vers l'infini, nous pouvons conclure, par comparaison, que un tend vers l'infini.
Dans le deuxième exemple, nous considérons la suite Vn = -n^2 - n + (-1)^n. Encore une fois, nous utilisons l'encadrement de (-1)^n entre -1 et 1 car cette fonction n'a pas de limite. Nous remarquons que le terme dominant est n^2, alors que (-1)^n n'a qu'un rôle mineur.
Nous faisons l'encadrement de Vn en ajoutant (-1)^n, puis nous obtenons une suite qui tend vers moins l'infini. En factorisant le terme de plus haut degré, nous obtenons Vn < n^2*(-1) + (-1/n) + (1/n^2). La partie de droite tend vers 1, alors que la partie avec le minus tend vers moins 1. Ainsi, n^2*(-1) - n + 1 tend vers moins l'infini.
En utilisant la comparaison avec une suite qui tend vers moins l'infini, nous concluons que Vn tend vers moins l'infini. Ainsi, ces deux exemples illustrent l'utilisation de l'encadrement pour traiter des suites impliquant des fonctions sinus ou (-1)^n.
Maths SM&SP
Analyse
2BAC SM Maroc
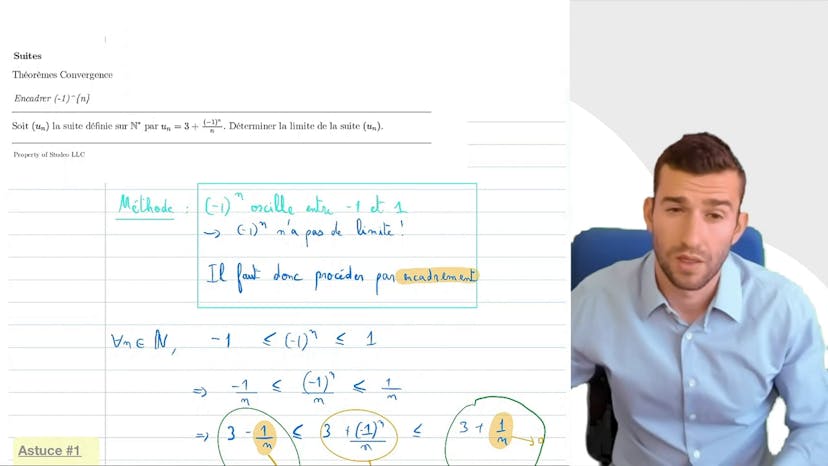
Encadrer (-1)^n
Dans ce cours, on étudie des suites où l'encadrement est nécessaire. Ces suites sont du type "(-1)^n/n" et n'ont pas de limite. Cependant, on peut les encadrer pour les analyser asymptotiquement. En utilisant cette méthode, on montre que la suite UN = 3 + (-1)^n/n tend vers 3. On utilise le théorème d'encadrement pour montrer cette convergence et trouver la limite. Le théorème d'encadrement est très puissant car il permet de prouver la convergence et de trouver la limite en même temps. Ici, par encadrement, on a prouvé que UN tend vers 3.


